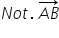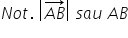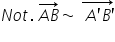Noțiunea de vector

în lecția aceasta vom prezenta

noțiunea de Vector iar pentru aceasta

este necesar să definim câteva

noțiuni introductive dacă avem

o dreaptă d pe care considerăm

un segment AB atunci dreapta d

se va numi dreapta suport a segmentului

vom numi direcție a dreptei D mulțimea

formată din dreapta d și din toate

dreptele paralele cu d Deci două

drepte au aceeași direcție dacă

sunt paralele sau coincide un alt

segment CD are aceeași direcție

cu AB Dacă dreptele lor suport

sunt paralele sau cu inchide Iată

alte exemple de segmente având

aceeași direcție MN și pq ele au

aceeași direcție de oarece dreptele

lor suport sunt paralele iar segmentele

r s și t e au aceeași direcție

pentru că dreptele lor suport coincid

o dreaptă d poate fi parcursă în

două sensuri de la a la b sau de

la b la a prin urmare pe segmentul

ab avem definite două sensuri iar

acesteia sunt sensuri opuse un

segment pe care a precizat și sensul

de parcurgere se numește segment

orientat de exemplu dacă alegem

sensul de la a la b atunci vom

indica chest lucru printre o săgeată

astfel și am obținut în acest mod

reprezentarea geometrică a segmentului

orientat AB acesta se notează astfel

a b cu 100 g atât deasupra săgeata

Indică orientarea de la a la b

prin urmare segmentul orientat

ab nu este același lucru cu segmentul

orientat Ba deoarece aceste două

segmente au sensuri diferite punctul

a se numește originea segmentului

orientat sau punctul de aplicație

iar b se numește extremitate sau

vârf am vorbit până acum despre

direcția și sensul unui segment

la un segment de mai interesează

și mărimea sau lungimea acestuia

așa cum știți lungimea segmentului

AB este distanța de la a la b lungimea

segmentului orientat AB se notează

astfel modul din AB egal cu a b

de lungimea segmentului orientat

sau modulul segmentului orientat

este lungimea segmentului AB în

continuare vom discuta despre segmente

echipolente două segmente orientate

se numesc echivalente dacă au aceeași

mărime direcție și sens Iată un

exemplu avem aici mai multe segmente

echipolente ab a prim b prim MN

și CD observăm că dreptele lor

suport sunt paralele prin urmare

aceste patru segmente au aceeași

direcție de asemenea ele au aceeași

lungime și același sens dacă segmentul

ab este echipă Olint cu segmentul

a prim b prim atunci vom nota acest

lucru astfel mod de suna acum un

alt segment care are aceeași lungime

cu AB o să notez cu RS aceeași

direcție în să observăm că cele

două segmente au sensuri opuse

prin urmare segmentele a b și r

s nu vor fi segmente echipolente

acum o să desenez un alt segment

pq care are aceeași direcție și

sens cu AB totuși cele două segmente

nu sunt echipolente pentru că observăm

că acestea au mărimi diferite prin

urmare segmentele echipolente din

această figură sunt ab a prim b

prim m n și c d și acum putem să

trecem la noțiunea de vector un

Vector este mulțimea tuturor segmentelor

orientate echipolente cu un segment

orientat dat domnul tau un Vector

cu ajutorul unui reprezentant al

acestei mulțimi de exemplu cu ajutorul

segmentului AB Iată acesta este

vectorul ab sau mai putem să învățăm

și astfel V cu o săgeată deasupra

modulul sau mărimea sau norma vectorului

AB este lungimea segmentului AB

vom nota astfel modulul vectorului

ab sau modulul vectorului V este

lungimea segmentului AB în continuare

discutăm despre vectorul nul vectorul

nul se notează cu 0 și o săgeată

deasupra iar acesta este vectorul

având lungimea egală cu zero prin

urmare modulul vectorului nul va

fi egal cu zero Deci originea acestui

Vector coincide cu extremitatea

un alt Vector important este vectorul

unitate se mai numește vers sau

Vector unitar putem să îl notăm

cu e modulul vectorului unitar

este egal cu 1 Așadar vectorul

unitate este vectorul având lungimea

egală cu 1 mai trebuie să definim

noțiunea de Vector egal Aceștia

sunt vectorii care au aceeași direcție

mărime și același sens prin urmare

doi vectori egali pot avea aceeași

dreaptă suport sau drepte suport

paralele dacă vectorul v este egal

cu vectorul u vom nota acest lucru

doi vectori sunt opuși dacă au

aceeași direcție mărime dar sensuri

opuse să vedem și un exemplu în

grafic pe această dreaptă suport

avem acest Vector V și un alt Vector

având aceeași direcție cu el aceeași

mărime dar sensuri opuse acesta

este vectorul opus și se notează

cu minus V la final să reținem

că un Vector este o mulțime infinită

de segmente orientate echipolente

cu un segment dat în lecțiile ce

urmează majoritatea conceptelor

geometrie vectorială se vor introduce

cu ajutorul reprezentanților vectorilor

dar este incorect să se identifice

vectorul cu un singur reprezentant

al său