Noţiuni de trigonometrie

în această lecție o să învățăm

câteva noțiuni de trigonometrie

În triunghiul dreptunghic cuvântul

trigonometrie provine din limba

greacă trigono înseamnă triunghi

și matran înseamnă măsură astfel

trigonometria este o ramură a matematicii

care studiază relațiile dintre

laturile și unghiurile unui triunghi

presupunem ca avem o stradă iar

nivelul acesteia crește la fiecare

200 m cu 3 m atunci raportul dintre

înălțimea străzii și drumul parcurs

poate fi considerat o măsură a

unghiului pe care drumul îl face

cu orizontala și o să vedem că

acest raport este constant notă

în vârful acestui unghi cu ei iar

aici o să mai fixez două puncte

B și C În triunghiul dreptunghic

ABC în calcularea portul dintre

înălțimea drumului și lungimea

parcursă observăm că înălțimea

drumului este o catetă În triunghiul

abc mai exact atâta opusă unghiului

A iar drumul parcurs adică distanța

AB este ipotenuză calculăm Așadar

în triunghiul ABC raportul dintre

cateta opusă unghiului a adică

BC supra ipotenuză a b acest raport

este 3 supra 200 o să mai fixez

aici alte două puncte m și n Acum

ne uităm în triunghiul a m n și

acesta este un triunghi dreptunghic

în n și calculăm din nou raportul

dintre înălțimea drumului și distanța

parcursă de mașină până în punctul

M în triunghiul a m n raportul

dintre cateta opusă unghiului a

și ipotenuza este m n supra a m

egal cu noua supra distanța parcursă

de mașină până în punctul m este

de 600 m putem să simplificăm această

fracție cu 3 și obținem 3 supra

200 observăm că am obținut aceeași

valoare a raportului dintre înălțimea

străzii și drumul parcurs de mașină

acest raport dintre cateta opusă

unui unghi ascuțit al unui triunghi

dreptunghic și ipotenuza este tot

timpul constant el nu depinde de

laturile triunghiului în care încadrăm

unghiul și doar de măsura unghiului

respectiv această constantă se

va numi sinusul unghiului a și

se notează cu sin de a prin definiție

sinusul unghiului a va fi raportul

dintre cateta opusă unghiului A

și ipotenuza acest aport este constant

pentru un unghi a având o măsură

dată observăm astfel că prin măsurarea

unghiurilor nu înțelegem doar măsurarea

acestora cu raportorul măsura unui

unghi este dată și de relația dintre

laturile triunghiului dreptunghic

din care provin a unghiul respectiv

putem defini în continuare și alte

rapoarte constante intru în triunghi

dreptunghic aceste rapoarte se

mai numesc și funcții trigonometrice

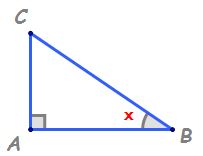
avem un triunghi dreptunghic și

am uitat laturile acestuia cu literele

mici a b și c iar Aici avem un

unghi ascuțit pe care îl am notat

cu X după cum am văzut anterior

sinus de x se definește ca fiind

raportul dintre cateta opusă unghiului

x și potenza în acest caz b supra

c un alt raport Constanța funcție

trigonometrică este funcția Cosinus

Cosinus de x este cateta alăturată

supra ipotenuză adică a supra c

tangenta unghiului x va fi cateta

opusă supra cateta alăturată unghiului

x adică b supra a iar cotangenta

unghiului x va fi raportul dintre

catetele tu rată supra cateta opusă

și egal cu a supra b nu face în

continuare un exemplu concret în

care vom calcula aceste funcții

trigonometrice Se dă triunghiul

dreptunghic ABC având laturile

cu lungimile de 3 4 și 5 cm calculând

mai întâi funcțiile trigonometrice

pentru unghiul b sinus de b este

cateta opusă unghiului B adică

AC supra ipotenuză bc egal cu 4

supra 5 cosinus de B este cateta

alăturată supra ipotenuză adică

a b supra bc și egal cu 3 supra

5 tangenta unghiului B este cateta

opusă a c supra cateta alăturată

AB egal cu 4 supra 3 și cotangenta

unghiului B este cateta alăturată

a b supra cateta opusă a c și egal

cu 3 supra 4 acum o să calculăm

funcțiile trigonometrice pentru

unghiul c sinusul unghiului c este

cateta opusă adică ab supra ipotenuză

supra bc egal cu 3 supra 5 cosinusul

unghiului c este cateta alăturată

supra ipotenuză ace supra bc egal

cu 4 supra 5 tangenta unghiului

c este cateta opusă a b supra ac

egal cu 3 supra 4 și cotangenta

unghiului c este cateta alăturată

a c supra cateta opusă a b egal

cu 4 supra 3 putem observa că sinus

de B este egal cu cosinus de ce

sinus de c este egal cu cosinus

de b tangenta unghiului b este

egală cu cotangenta unghiului c

și tangenta unghiului c este egală

cu cotangenta unghiului B