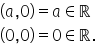Numere complexe (noțiuni introductive)
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție ne vom opri asupra
numerelor complexe astfel prin
introducerea numerelor reale se
pot exprima rezultatele oricăror
măsurători dar problema soluțiilor
de orice tip cu accent si real
nu este rezolvat afirmația de mai
sus este fundamentată pe situații
clar întâlnite situații în care
rezolvarea unor ecuații simple
nu au avut soluții determinate
deoarece întâlneam situația nu
avem soluții real cel mai bun exemplu
sunt ecuațiile de gradul al doilea
ecuații la care în momentul în
care ne propunem să determinăm
soluții și că Steam Delta negativ
afirmam întradevăr că soluțiile
nu se îndreaptă în această situație
se pune problema necesității extinderii
noțiunii de număr extindere Ce
presupune un număr care nu este
doar un număr real și el să fie
exprimat întru altă manieră să
vedeți mai largă mai vastă aceea
de număr complex așa după cum am
acceptat ideea apartenenței numerelor
jale la mulțimea numerelor reale
vom accepta în continuare ai de
apartenență a numerelor complexe
la mulțimea numerelor complexe
este importantă înainte de toate
Să înțelegem că numerele complexe
nu sunt rezultatul unor măsurători
ca în cazul numerelor reale acest
fapt a trage de la sine o abstractizare
o tratare mai mulți formală a teoriei
număr complex în pofida acestui
grad de abstractizare a noțiunilor
teoria numerelor complexe are un
foarte înalt grad de utilitate
în aplicațiile practice întâlnite
în mecanică fizică electrotehnică
și altele Definirea numerelor complexe
fie produsul cartezian a r o r
Deci mulțimea numerelor reale înmulțită
cu produs cartezian cu mulțimea
numerelor reale definită de mulțimea
perechilor ab cu a respectiv pe
din R deci practic primul ei este
din primul rb1 Da este din al doilea
R punem mulțimea perechilor ordonate
de numere reale este important
să precizez că a b ca și pereche
este egal cu a prim b prim dacă
a egal cu a prim respectiv b egal
cu b prim pe la aceste condiții
câteva exemple dacă vin și spun
2 aparține lui R 1 aparține lui
r înțeleg că perechea 2 1 aparține
lui r ori e astfel în mulțimea
numerelor reale am axa numerelor
reale la axa pe care putem să Reprezentăm
oricare din acest filme reale de
pildă doiul Da 1 minus trei da
ar fi pe undeva pe aici 3 în momentul
în care facem produsul cartezian
a Roller apare așa numitul sistem
de axe x o y astfel prima axa reală
este cea frântă primului ayrton
produsul cartezian cea de axa reală
este aferentă celui de al doilea
este produsul cartezian pe prima
axă reprezintă elemente reale ca
asa În egală măsură elemente reale
ați auzit Cu siguranță de de ideea
de sistem cartezian x o y astfel
acesta este x pe care știm 0 e
cu pe care îl știi minus 3 3 este
un punct din sistemul cartezian
x o y care În egală măsură aparține
produsului cartezian a Roller și
mai decât atât se reprezintă ca
perechea ordonată de numere reale
minus 3 3 la fel 2 și 1 iar perechea
2 1 aparține lui r o r respectiv
1 minus 3 perechea ordonată 1 minus
3 aparține produsului cartezian
r ori el în continuare pe mulțimea
A Roller se definesc două operații
algebrice adunarea perechilor ordonate
de numere reale respectiv înmulțirea
perechilor ordonate de numere reale
pentru Zet egal cu Perechea ordonată
ape și zet prim egal cu Perechea
ordonată c d cu d respectiv d prim
din produsul cartezian a Roller
da vom face adunarea de tuse primi
ca fiind ab perechea ordonata b
plus perechea ordonată c d e care
are drept rezultat a plus c Deci
prima poziție cu prima poziție
Da respectiv a doua poziție a perechi
rezultate Ricky ordonate rezultat
bala Dunării b atunci când ne propunem
să facem un mulți rea perechilor
ordonate de numere reale a b perechea
înmulțită perechea c d avem dreptul
rezultat a c minus b d pe prima
poziție respectiv a d plus b c
pentru o lămurire mai exactă a
acestor noțiuni o să dau câteva
exemple adunarea perechi ordonate
Y32 cu Perechea ordonată minus
unu trei am lămurit a plus c a
este 3 c este minus 1 astfel 3
plus minus 1 respectiv a doua poziția
perechi ordonate doi plus trei
astfel rezultatul sumei perechilor
ordonate 3 2 cu minus 1 3 este
2 5 perechea ordonată 2.5 dacă
dorim să le înmulțim formula în
față Da avem 3 înmulțit cu minus
1 minus spune formula 2 înmulțit
cu 3 prima poziție a doua poziția
perechi ordonate Pa Fie ad a desemnând
3 înmulțit cu 3 plus b c adică
2 înmulțit cu minus 1 minus 3 minus
6 respectiv 9 și minus 2 rezultatul
final fiind minus 9 respectiv 7
până la 3:00 la exemplu tot pentru
adunare În cazul ăsta 2 și minus
unu perechea ordonată 2 minute
adunată cu Perechea ordonată minus
3 1 2 minus 3 respectiv minus unu
plus unu astfel obține perechea
ordonată minus unu zero produsul
acestor două perechi ordonate după
formula mai sus menționată A2 orice
ottignies 3-a minus b minus 1 ori
de 1 respectiv 2 a umplut minus
1 ori minus 3 minus 5 Definiți
fiecare element al mulțimii R o
r Deci produsului cartezian al
pe care sunt definite operațiile
epice prezentate mai sus practică
adunarea respectiv înmulțirea se
numește număr complex se notează
cu c barat mulțimea numerelor complexe
și practic si ul este produsul
cartezian erori aer unde se reprezintă
mulțimea elementelor z în care
sau cu proprietatea că se este
perechea ordonată ape cu a respectiv
b aparținând numerelor reale în
particular numerele complexe zero
zero și unu zero sunt de fapt numere
reale 0 respectivul astfel zero
zero este punctul o 1 0 este punctul
A dacă îmi ia și propune nu știu
trei zero este punctul P respectiv
minus doi zero este punctul de
toate acestea sunt numerele reale
aflat pe axa reală reamintim că
asta este o axă reală Da practică
x Da deci sunt numere reale de
forma 0 0 0 1 0 practică numărul
real 1 3 0 numărul de trei respectiv
minus doi zero numărul real minus
2 astfel orice element de formă
a 0 este de fapt numărul real a
adunarea a două numere reale dar
scrise ca perechi din si dati mulțimea
numerelor complexe se Rezumă la
a aduna practic perechea a 0 cu
Perechea pe 0 unde a 0 a murit
este numărul real a da respectiv
b 0 este numărul real b este egală
cu a plus b respectiv 0 plus practică
a plus b și 0 a plus b egal că
discutăm despre număr real înmulțirea
pe același principiu după formula
noastră mai sus comentată a b da
ar fi 0 0 minus respectiv a 0 și
pi zero practică a b a b Fie acel
număr rate care comenta în continuare
vom discuta despre proprietății
portante ale operațiilor algebrice
cu numere complexe astfel elementul
neutru pentru adunare este 0 scris
ca perechea 00 din numere complexe
Da ținea numerelor complexe astfel
pentru orice zi din mulțimea număr
complex numărul complex ape sau
perechea ape cu a și p aparține
lui r va fi adunat cu acest 0 element
neutru 10 plus zero este de fapt
perechea ab plus zero care e zero
zero cartonată cunoaștem că a plus
b plus 0 Da respectiv a b darob
e chiar z înțeleg de aici că z
plus zero este z Deci element neutru
pentru adunare întrucât adunarea
acestuia la orice număr complex
are ca rezultat acel număr complex
element opus sau opusul minus z
minus 10 minus A minus pe perechi
ordonate astfel pentru orice timp
ce de formă se taie perechea ordonată
ab cu a și pe reale plus minus
sat Buda este egal cu Perechea
b plus perechea minus a minus b
astfel a minus respectiv b minus
b practic rezultatului zero zero
adică acel 0 elementul neutru determinat
mai sus elementul neutru pentru
înmulțire este 1 1 definit ca fiind
perechea ordonată un urs oricare
ar fi sat aparținând lui c cu d
egal cu eb perechi Ordonați și
pe aparține lui r z înmulțit plătesc
data asta e pentru înmulțire daca
e operația algebrică astfel înmulțit
cu 1 este perechea ab înmulțită
cu unu adică perechea ortona t10
conform formulei mai sus comentate
a înmulțit cu 1 minus b înmulțit
cu 0 respectiv a înmulțit cu 0
plus B1 țigan astfel rezultatul
obținut este a b apei fiind numărul
10 Numărul complex de la care am
plecat elementul invers Sau inversului
spune este acela în care Zet înmulțit
cu 10 la minus ar fi egal cu 10
la mincinos și egal cu unu unu
fiind neutru pentru înmulțire practic
Zet calculate sat la minus 1 ar
fi Unix y7 reci ordonată cu a b
x respectiv igrec rea avem 10 la
minus 1 egal cu a b perechi ordonată
înmulțită cu x y pe de coordonată
conform formulei de înmulțire este
egal cu a x minus y respectiv a
y din care se obține valoarea lui
x ca fiind a supra a pătrat plus
b pătrat prin înlocuirea lui x
în cea de a doua ecuația sistemul
obținem că y este egal cu minus
b supra a pătrat plus b pătrat
pur și simplu Axel se înlocuiește
în ecuația 2 astfel prin determinarea
a lui x respectiv y înțelegem de
fapt cum determinat elementul invers
sau inversul unui număr complex
de formă a b perechi ordonate a
b c dacă z aparține lui c și el
este definit ca perechi ordonată
ape cu z divide diferite 0 atunci
sat la minus unu sau inversul lui
z este perechea ordonată a supra
a pătrat de pătrat și minus pe
supra a pătrat plus b pătrat

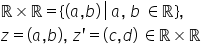
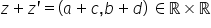
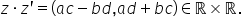
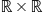 pe care sunt definite operațiile algebrice prezentate mai sus se numește număr complex. Mulțimea numerelor complexe este mulțimea:
pe care sunt definite operațiile algebrice prezentate mai sus se numește număr complex. Mulțimea numerelor complexe este mulțimea: