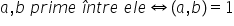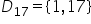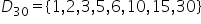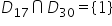Numere prime între ele (c.m.m.d.c =1)

cu b A intersectat cu d b vom nota

mulțimea divizorilor comuni ai

numerelor a și b iar cu m a intersectat

cu m b o să notăm mulțimea multiplilor

comuni ai numerelor a și b o să

folosim aceste două notații pentru

cel mai mare divizor comun respectiv

pentru cel mai mic multiplu comun

al numerelor a și b avem următoarea

definiție două numere naturale

a și b se numesc prime între ele

dacă cel mai mare divizor comun

al acestora este 1 8 dau un exemplu

Scrie mulțimea divizorilor numărului

17 17 este un număr prim Acesta

are exact doi divizori Aceștia

sunt 1:17 acum să scrie mulțimea

divizorilor numărului 30 Aceștia

sunt 1 2 3 cinci șase De ce 15:30

Cum putem să verificăm dacă am

scris toți divizorii numărului

31 toarea întotdeauna mulțimea

divizorilor unui număr natural

conține un număr par de elemente

Deci numărați elementele acestei

mulțimi și asigurații va că avem

un număr par de elemente apoi dacă

scrie ma cinci divizori în ordine

crescătoare procedăm în felul următor

înmulțim primul număr ultimul iar

rezultatul înmulțirii va trebui

să fie 30 continuăm cu al doilea

număr și penultimul 218 este 30

continuăm cu 3 și 10 trei ore zece

este 30 iar cinci ori 6 este 30

Asta este modalitate destul de

rapid de de a verifica dacă am

scris toți divizorii unui număr

natural acum să intersectăm cele

două mulțimi mulțimea divizorilor

numărului 17 intersectată cu mulțimea

divizorilor numărului 30 este în

mulțimea formată din elementul

1 observăm că unul este singurul

element comun al celor două mulțimi

spune ma speli că cel mai mare

divizor comun al acestor numere

17:30 este 1 iar în acest caz numerele

17:30 se numesc prime între ele