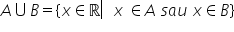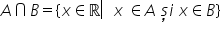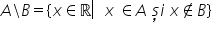Operații cu intervale de numere reale

să vedem acum Ce operații putem

face cu intervalele de numere reale

și haide să ne amintim Ce este

un interval avem aici intervalul

minus 2 3 deschis la stânga și

închis la dreapta pe un interval

este de fapt o mulțime de numere

reale fiind o mulțime înseamnă

că putem să facem și cu intervale

operațiile pe care le am învățat

la mulțimi și avem acest exercițiu

vrem să găsim toate numerele reale

care sunt mai mici sau egale cu

3 și strict mai mari ca minus 1

pentru aceasta ne vom ajuta și

de axa numerelor Iată și am reprezentat

aici și unitatea de măsură bun

vrem să găsim acele numere care

sunt în același timp mai mici sau

egale cu 3 fii Street mai ca minus

unu Păi Haideți să Reprezentăm

pe axa mulțimea acestor numere

care sunt numerele mai mici sau

egale cu 3 și atât avem aici numărul

0 1 2 3 este aici numerele mai

mici sau egale cu 3 sunt acestea

Deci vom reprezenta aici avem minus

infinit și aici 3x poate se și

valoarea trei deci de fapt ce am

obținut avem un interval nemărginit

închis la dreapta avem intervalul

minus infinit 3 bun acum x trebuie

să fie în același timp mai mare

strica minus unu sual așezăm pe

axa pe minus unu și să vedem care

sunt numerele strict mai mari ca

minus unu Aici este 0 Aici îl avem

pe minus unu mult numerele strig

mai mari ca minus unu sunt acestea

începem de la minus 1 că trei plus

infinit de ceai de să notăm aici

plus infinit tot așa am obținut

un interval nemărginit Însă acum

observăm că x nu poate să iau valoarea

minus tu nu Deci avem un interval

deschis la acest capăt intervalul

minus 1 plus infinit Păi numerele

reale pe care noi le căutăm trebuie

să facă parte din acest interval

dar și din acesta ia ată cuvântul

și ne arată că între aceste două

mulțimi Ce operație trebuie să

facem operația de intersecție intersecția

acestor două mulțimi ne vada numerele

reale care fac parte din ambele

intervale și Haideți să vedem care

este intersecția acestor două intervale

Păi unde avem pe axa ambele culori

adică și albastru galben iată în

această zonă Aici sunt numerele

care fac parte și din acest interval

dar și din acesta și atunci Haideți

să notăm avem capetele minus 1

și 3 Cum este la minus 1 minus

unu face parte din acest interval

se vede Da însă minus unu nu face

parte din intervalul reprezenta

cu galben avem deschis la minus

1 Deci trecem aici interval deschis

iar numărul 3 face parte din acest

interval avem paranteză pătrată

și e clar că face parte și din

această mulțime de ce aici punem

paranteză pătrată De fapt am respectat

parantezele care apar aici avem

intervalul deschis la stânga închis

la dreapta minus unu trei să găsim

acum toate numerele reale care

sunt mai mari sau egale cu minus

2 și scrii mai mici ca 6 și ele

să fie și mai mari sau egale cu

1 și mai mici sau egale cu 7 și

ne ajutăm și de axa numerelor Deci

căutăm numerele reale care verifică

a ambele relații aici x trebuie

să fie mai mare sau egal cu minus

2 și strig mai mic ca 6 ce avem

avem un interval de numere reale

minus doi șase cu Mix ia și valoarea

minus doi înseamnă că avem un interval

închis minus 2 și deschis la 6x

nu poate sa ia valoarea șase aici

x este mai mare sau egal cu 1 și

mai mic sau egal cu 7 Deci avem

intervalul închis unu șapte bun

cuvântul și ce ne arată ne arată

că Numerele pe care le căutăm trebuie

să facă parte din ambele intervale

Deci aici trebuie să intersectăm

aceste două intervale cu alte cuvinte

vom face intersecția acestor două

mulțimi să vedem acum să trasăm

prima mulțime Deci primul interval

minus doi șase unde e minus doi

avem aici minus 1 minus 2 1 2 3

4 5 6 este aici și să trasăm acest

interval minus doi șase bun la

minus doi avem paranteză pătrată

este un interval închis la stânga

și deschis la dreapta intervalul

1 7 să schimbăm și culorile avem

aici 1 dacă Aici este 6 înseamnă

că aici este 7 și să trasăm acest

să Reprezentăm acest interval bun

avem un interval închis Deci trecem

și pe desen care sunt acum numerele

reale care verifică în care fac

parte din ambele mulțimi unde avem

ambele culori iată în această zonă

și ce capete avem pentru că am

o tot un interval Deci egal mai

departe cu avem 1 și 6 la 1:00

avem un interval închis iar la

6:00 este interval deschis pentru

că Iată 6 face parte din această

mulțime din acest interval însă

nu face parte din acesta de aceea

aici am trecut paranteză rotundă

Deci am ținut intervalul 1 6 închis

la stânga deschis la dreapta următorul

exemplu se găsim acum toate numerele

reale care verifică acestei două

relații simultan asta ne arată

cuvântul și că trebuie să fie îndeplinite

ambele relații Deci fix trebuie

să fie mai mare strict ca minus

doi și mai mic sau egal cu 1 și

eu trebuie să fie și mai mare sau

egal cu 1 și mai mic sau egal cu

4 Păi dacă x trebuie să fie în

același timp mai mic sau egal cu

1 dar și mai mare sau egal cu 1

Ce înseamnă asta înseamnă că x

nu poate să ia decât o valoare

x este egal cu unu sigur acest

lucru poate fi foarte ușor observat

și folosind un de intersecția intervalelor

Iată avem aici intervalul minus

2 1 închis da minus 2 pardon deschis

la minus 2 și în chizda 1 și avem

aici intervalul închis 1 4 cuvântul

și ne arată că trebuie să facem

intersecția acestor două intervale

și Haideți să trecem mai întâi

a minus 2 1 x minus unu Aici este

minus 2 aici este 1 treceai de

să trasăm acestea interval bun

avem aici deschis iar aici Este

închis 1 4 Păi pe unul deja la

întrecut 2 3 4 întrecem aici și

să transform și acest interval

avem aici cu un interval Păi Ce

observăm Folosind un echer de acest

desen e ușor de văzut că numărul

1 face parte din acest interval

dar tot unu face parte și din acest

interval de timp un număr care

face parte din ambele intervale

este 1 venim și notăm egal cu mulțimea

formată din elementul iată că în

cazul intersecției unor intervale

putem să obținem chiar și mulțimi

finite sau putem să avem acest

exemplu iar să găsim numerele reale

care verifică faptul că x este

strict mai mare ca minus 2 și mai

mic sau egal cu 1 și în același

timp x este strict mai mare ca

1 și mai mic sau egal cu 4 Păi

Ce observăm x este mai mic sau

egal cu 1 și în același timp și

strig mai mare ca 1 se poate așa

ceva Nu aici nu avem soluție deci

putem să notăm că x aparține mulțimii

cu Feed dacă ne folosim de intervale

piață avem intervalul minus doi

unu exact cum era mai sus însă

aici intervalul sa schimbat nu

mai avem un interval închis și

el este un interval deschis la

stânga e clar și din desen că 1

aparține acestui interval dar avem

aici interval închis însă unul

numai aparține și acestui interval

Deci intersecția celor două intervale

este mulțimea vidă Deci Iată două

exemple în care intersecția intervalelor

na dat aici o mulțime finită și

aici mulțime chiar Vida sau putem

să avem acest tip de exercițiu

să determinăm toate numerele reale

astfel încât x să fie strict mai

mare ca 3 sau x să fie mai mare

sau egal cu minus doi Păi cuvântul

sau ce înseamnă înseamnă că x trebuie

să aparțină cel puțin uneia dintre

aceste două mulțimi Deci aici vom

vorbi de reuniune de intervale

dacă x este strict mai mare ca

3 ce interval avem Păi ID să îl

trecem pe trei avem aici unu doi

trei numerele mai mari ca trei

sunt poziționate în această parte

axa numerelor Deci avem x a să

fie strict mai mare ca 3 Deci obținem

un interval nemărginit și deschis

la acest capăt avem trei plus infinit

bun notăm aici plus infinit x să

fie mai mare sau egal cu minus

2 minus trecem pe minus 2 aici

mai mare sau egal cu minus 2 înseamnă

că pornim de la minus 2 și mergem

către plus infinit tot așa avem

un interval nemărginit chiar acum

El este închis la acest capăt intervalul

minus 2 plus infinit și să vedem

ce obținem Deci noi vrem acele

numere reale care aparțin cel puțin

uneia dintre aceste două mulțimi

Păi unde pe desen avem măcar o

culoare cel puțin o culoare păi

avem aici dar avem și aici sigur

is în două culori noi știm că vrem

să avem cel puțin una de ce această

parte bună Păi ce obținem tot Acest

interval Da minus 2 plus infinit

10 Reuniunea acestor două intervale

este minus 2 plus infinit era și

normal să obținem așa De ce anume

pentru ca acest interval dar este

inclus în acesta se vede foarte

ușor și pe desen alt exemplu să

găsim tu numerele reale pentru

care x este mai mare sau egal cu

minus 5 și strig mai mic decât

3 sau x este mai mare strica minus

1 și mai mic strict decât patru

pe ce interval avem aici avem minus

5 3 închis la acest capăt deschis

la acesta cuvântul sau înseamnă

că trebuie să facem reuniune pentru

între cele două intervale și avem

aici Haideți chiar să lase zi ceva

mai potrivit și aici avem intervalul

deschis minus unu patru bun și

Haideți să le Reprezentăm pe axa

avem minus 5 3 minus 1 minus 2

minus 3 minus 4 minus 5 este aici

avem 1 2 3 acesta este intervalul

minus 5 3 aici avem închis Și aici

este deschis minus 1 4 să schimbăm

și culoarea e c minus Aici este

4 și să îl trasăm minus 1 4 interval

deschis bun noi facem reuniune

între aceste două intervale Deci

Vrem să vedem care sunt numerele

reale care sunt în cel puțin unul

din aceste două intervale unde

avem cel puțin o culoare mă refer

la albastru sau la roz poiată aici

avem albastru Deci acest interval

ne convine aici avem ambele culori

ne convine și acesta aici avem

praz E bun și acesta și atât de

fapt ce obținem Păi avem un interval

cu capetele minus 5 și 4 egal cu

minus 5 4 respectăm paranteze la

aici avem paranteză pătrată Deci

avem interval închis la stânga

și deschis la dreapta am obținut

acest interval sau putem să avem

acest tip de exercițiu vrem să

ne unim intervalul deschis minus

unu unu cu acest interval băiat

aici avem intervalul minus unu

unu și aici intervalul doi șase

Reuniunea acestor două intervale

ne dă chiar intervalul acesta reunit

cu acesta Prin Reuniunea lor nu

se obține acum un al treilea interval

de aceea rezultatul rămâne scris

sub această formă sau mai putem

să întâlnim un alt tip de exercițiu

din acest interval minus 5 2 pe

care il am de prezentat și pe axa

să scădem două elemente și cele

două elemente din această mulțime

0:01 Iată Aici este 0 și aici este

unul dacă din acest interval scoate

m aceste două numere atunci cine

rămâne Putem să scriem sub formă

de reuniune de intervale vom obține

avem aici de la minus cinci la

zero avem un interval Deci minus

cinci zero Evident la zero vom

trece deschis pentru că am scos

pe 0 din această mulțime apoi avem

intervalul deschis 0 1 dec reunit

cu acest interval deschis q01 Ce

conține toate numerele cuprinse

între zero și unu fără să le luăm

în calcul pe zero sau pe 1 și mai

avem acest interval deschis 1 2