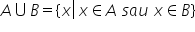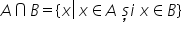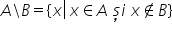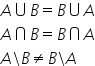Operații cu mulțimi- reuniune, intersecție, diferență

să vedem acum Ce operații putem

să facem cu mulțimi si O să vedeți

că vom avea trei tipuri de operații

posibile și să începem cu un exemplu

simplu avem mulțimea mare formată

din elementele 2 1 și 4 și mulțimea

b mare formată din elementele 1

5 și 4 și 8 și idee să facem și

diagrama de aici vom notam elementele

mulțimii A mare 2 1 și 4 și aici

elementele mulțimii B mare și avem

un sha1 bun însă unul deja la întrecut

Deci unul trebuie să facă parte

și din mulțimea b mare cinci patru

patru este și aici nu mai scriem

și 8 Deci așa asta e ce am încercat

mulțimea A mare și mulțimea b mare

este aceasta Bun prima Operație

pe care o discutăm este Reuniunea

a doua mulțimi Reuniunea se notează

cu acest semn este un arată ca

un 8 la aici îmi scrie prima mulțime

de exemplu mulțimea A mare și aici

cea de a doua mulțime mulțimea

b mare și citim a reunit cu b Ce

înseamnă Reuniunea a doua mulțimi

este tot o mulțime care conține

toate elementele mulțimii A și

toate elementele mulțimii B Deci

mai întâi Haide să scriem elementele

din mulțimea A fiind o mulțime

trecem acolada și Avem doi unu

și patru am scris elementele mulțimii

A și acum trebuie să scriem elementele

din mulțimea b și avem 1 Păi e

corect să scriem așa De ce nu este

bine pentru am spus că a reunit

cu b este o mulțime și noi știind

că o mulțime când o mulțime elementele

trebuie să fie cam distincte adică

diferite Deci odată ce îl am pe

1 aici nu vă mai trece încă o dată

cinci patru patru deja este nu

mai scriem și 8 Deci am obținut

elementele 2 1 4 5 și 8 acum dacă

ne uităm pe diagramă mulțimea A

reunit cu b este de fapt această

mulțime pe care o Reprezentăm să

spunem așa cu galben Deci ce am

obținut Aici este mulțimea A reunit

cu b Adică am trecut de fapt toate

aceste elemente având grijă să

fie scrise fiecare o singură dată

dacă trecem b reunit cu a disc

este același lucru sigur fie a

reunit cu b f e b reunit cu a ne

va da aceeași mulțime următoarea

operație este intersecția a două

mulțimi intersecția se notează

cu 1 întors A deci acest semn și

trecem aici mulțimea A și mulțimea

b ce am obținut citim a intersectat

cu b și aceasta este tot o mulțime

care atenție conține doar elementele

comune celor două mulțimi pe elementele

comune Se pot observa foarte ușor

pe diagramă Care sunt elementele

care sunt și în mulțimea A și în

mulțimea B Păi chiar acestea care

ia Tot sunt cuprinse în ambele

diagrame ce avem aici reprezintă

intersecția mulțimii A cu mulțimea

b intersecția celor două mulțimi

Deci venim și notăm avem elementele

1 și patru nu e neapărat nevoie

să facem diagrame când calculăm

intersecția sau Reuniunea mulțimilor

putem să observăm intersecția celor

două mulțimi și de aici Iată mulțimea

a conține elementul doi doi nule

regăsim aici însă unu îl regăsim

la fel și pe patru deci singurele

elemente comune celor două mulțimi

sunt acestea a doua unu și patru

Dacă facem invers b intersectat

cu A vom obține aceeași mulțime

sigur vom avea tot așa elementele

1 și 4 acum să știți că există

și mulțimi care nu au elemente

comune de exemplu mulțimea C formată

din elementele 1 și 2 și mulțimea

de mare formată din elementele

3 și 4 Păi dacă ar fi să le Reprezentăm

cu ajutorul diagramelor aici avem

mulțimea și aceasta este mulțimea

de care are elementele 3 și 4 avem

elemente comune Nu însă aceasta

nu ne împiedică să facem intersecția

acestor două mulțimi c intersectat

cu d c obținem este tot o mulțime

însă ea nu are niciun element pentru

că nu există elemente care să fie

și în ce și în d Deci intersecția

lor este multimea Vida asemenea

mulțimi care au intersecția mulțimea

vidă se numesc Deci cum e cazul

acestora se numesc mulțimi disjuncte

de ceai de să scrie mic și mulțimi

disjuncte Deci mulțimi a căror

intersecție este mulțimea vidă

următoarea operație Diferența a

două mulțimi semnul pe care îl

folosim pentru diferență este acesta

sau pur și simplu un minus și avem

aici a minus b sau această notație

a minus b voi folosi prima notație

Și acum ce este diferența a două

mulțimi Păi obținem tot o mulțime

care atenție însă are doar elementele

mulțimii A și nu are elemente din

mulțimea B de sunt doar acele elemente

care sunt în A și nu sunt în b

pe ușor să le găsim pe diagramă

Iată toate elementele care sunt

în mulțimea A și nu sunt conținute

în b Păi avem doar unul singur

adică acesta numărul 2 această

parte asta înseamnă că este mulțimea

formată din elementul 2 ce spune

dacă facem Invers adică b minus

a vom obține același lucru adică

tot mulțimea formată din elementul

2 Păi Haideți să ne uităm puțin

dacă avem din dacă din b scoatem

toate elementele care care sunt

în ei adică toate acestea cine

rămâi doar elementele 5 și 8 a

stai înseamnă de fapt d minus aceasta

este mulțimea formată din aceste

două elemente de ce ai de să reținem

că dacă în cazul reuniunii a reunit

cu b era același este același lucru

cu b reunit cu a în cazul intersecției

a intersectat cu b a aceleași lucru

cu b intersectat cu A deci putem

să schimbăm fără problemă locul

mulțimilor a minus b în cazul diferenței

a minus b este diferit de b minus

ai clar că obținem mulțimi diferite

Haideți să facem o recapitulare

10 Reuniunea a doua mulțimi și

avem aici exemplul făcut A reunit

cu b de fapt la modul general vorbind

când avem două mulțimi oarecare

le notezi tot a și b dar ele sunt

mulțimi oarecare nu neapărat acesteia

notate de noi sus atunci ce înseamnă

a reunit cu b p este tot o mulțime

formată din elementele x cu Ce

proprietate pe aici am avut elementele

care erau din mulțimea a sau din

mulțimea b și la am pus pe toate

la un loc Deci este formată din

elementele x cu proprietatea că

x aparține mulțimii a sau x face

parte din mulțimea B Deci aparține

mulțimii B intersecția a două mulțimi

dacă avem din nou două mulțimi

oarecare pe care le notăm tot așa

a și b a intersectat cu b este

tot o mulțime formată din Ce elemente

elementele x cu Ce proprietate

poiată am avut Aici Doar elementele

comune care erau și în A și în

b Deci x cu proprietatea că x aparține

mulțimii A atenției și Deci trebuie

neapărat să trecem și x aparține

mulțimii B aici am avut sau pentru

că elementele erau fie din a fi

din b aici trebuie să fie din ambele

mulțimi și din a și din b diferența

dacă avem tot așa două mulțimi

a minus b este o mulțime care conține

acele elemente x cu Ce proprietate

cu proprietatea că Iată x aparține

doar mulțimii A dar nu aparține

și mulțimii B Deci x face parte

din a și x în același timp nu trebuie

să facă parte din mulțimea b și

acum Haideți să facem un exercițiu

să facem toate aceste operații

și avem mulțimea A mare reprezentată

de acele elemente x cu proprietatea

că x este număr par și x este mai

mic sau egal cu opt și avem și

mulțimea b care este formată din

elementele x cu proprietatea că

x este număr natural de Newton

că x aparține mulțimii numerelor

naturale și 2 este mai mic sau

egal cu x și strict mai mic decât

6 acum pentru a face operațiile

învățate cu aceste două mulți mai

întâi trebuie să enumerăm elementele

fiecărei mulțimi în parte ne ocupăm

de mulțimea a care sunt acele numere

pare mai mici sau egale cu 8 începem

de la zero urmează 2 4 6 îl trecem

și pe 8 Dar pentru că avem aici

mai mic sau egal și 8 aceste e

ultimul pentru mulțimea B căutăm

numerele naturale care sunt Cum

vedem că x este mai mare sau egal

cu doi și este strict mai mic decât

6 deci pornind de la 2:00 pentru

că avem mai mare sau egal urmează

3 4 numărul 5 verifică și el această

relație și mai chemi și pe șase

nu pentru că avem x este strict

mai mic decât 6 deci mergem până

la 5:00 și acum haide să facem

reuniune acestor două mulțimi A

unit cu b ce vom obține un om o

mulțime care conține atenție elementele

mulțimii A și ale mulțimii B puse

la un loc și trebuie să avem grijă

ca fiecare element să fie scris

o singură dată Asta înseamnă mulțime

descriem elementele din mulțimea

A și avem 0 2 4 6 și 8 tot ce am

avut aici a fost în mulțimea urmează

apoi să trecem elementele din mulțimea

m b-2 însă nu mai trecem pentru

că deja avem trei observăm că trei

nu este Deci trecem 4 este deja

și 5 și am obținut aici această

mulțime este Reuniunea mulțimilor

a și b intersecția lor a intersectat

cu b vom alege Acum doar elementele

comune celor două Deci doar acele

elemente care sunt și în A și în

b Păi Haideți să vedem 0 este în

ei dar nu este în B2 este în ei

este și în B4 la fel și atât Deci

vom avea pardon 2 și 4 Deci doar

acestei două elemente diferența

face mai întâi Diferența a minus

b căutăm prin urmare acele elemente

care sunt în mulțimea A și Atenție

nu sunt în mulțimea b 0 este în

a este și în b nu deci putem să

îl trecem 0 2 este în mulțimea

a este și în b noiembrie 4 la fel

este și în b nu e bunicel 6 este

în ei și nu e în V8 este în această

mulțime și nu e în b Deci îl trecem

și pe 8 b minus a căuta acum acele

elemente care sunt în mulțimea

b și nu sunt în mulțimea A 2 este

și în a avem trei și cinci doar

acestea două sunt în baie și nunta

3:05 și apă cu aceasta am încheiat

am făcut și Reuniunea și intersecția

și diferența acestor mulțimi