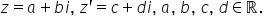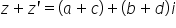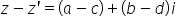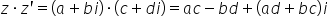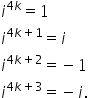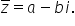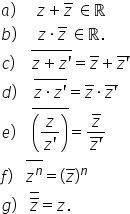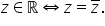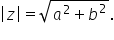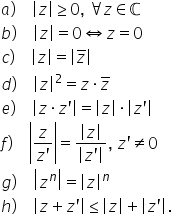Operații cu numere complexe (forma algebrică)

în această secvență vom rezolva

câteva operații cu numere complexe

un număr complex z are forma algebrică

a plus b e a este partea reală

iar b se numește partea imaginară

conjugatul său are forma algebrică

a minus b e Deci se schimbă semnul

doar la parte imaginară modulul

unui numar complex este radical

din partea reală la pătrat plus

parte imaginară la pătrat și trebuie

să rețineți că e pătrat este egal

cu minus unu în continuare să rezolvăm

acest exercițiu Se dau numerele

complexe Z 1 egal cu 4 plus 3 y

și z 2 egal cu 1 minus e la punctul

A trebuie să calculăm conjugatul

conjugatului numărului complex

Z 1 o să mai scriu încă o dată

numărul Z1 este 4 plus 3 e mai

întâi vom scrie Z1 conjugat și

egal cu 4 minus 3 e acum conjugatul

conjugatului numărului complex

Z 1 va fi egal cu 4 plus 3 i am

schimbat din nou semnul părții

imaginare observăm astfel că numărul

complex Z 1 conjugat de două ori

are aceeași formă algebrică cu

numărul unu Aceasta este o proprietate

importantă a numerelor complexe

Așadar este bine să rețineți că

numărul z conjugat de două ori

este egal cu z la punctul B trebuie

să calculăm Z1 plus 10231 plus

Z2 este egal cu 4 plus 3x plus

1 minus i Roma adunat mai întâi

părțile reale avem 4 plus 1 egal

cu 5 iar 3-a minus e este egal

cu 2 la punctul ce trebuie să calculăm

modul din Z 1 minus 2 Mai întâi

vom calcula diferența Z1 minus

Z2 și avem patru plus 3x minus

1 minus e egal cu 4 plus 3 minus

1 plus y egal 4 minus 1 este 3

iar 3a plus e este 4 in și acum

vom calcula modul din Z 1 minus

z 2 egal cu modul din 3 plus 4

egal cu radical din 3 la a doua

plus 4 la a doua egal 3 la a doua

este 9 4 la a doua 16 9 plus 16

este 25 iar adică el din 25 este

egal cu 5 vom continua cu punctul

d trebuie să calculăm Z1 plus Z2

conjugat mai întâi voi calcula

2 conjugat dată Z2 este 1 minus

e atunci Z2 conjugat va fi 1 plus

e și acum calculăm 10 unu plus

de doi conjugat vom avea patru

plus 3 plus 1 plus 4 plus 1 este

5 3-a plus e este 4 la punctul

E trebuie să calculăm modul din

Z 1 ori Z 2 Mai întâi vom calcula

produsul Z1 ori Z2 și avem patru

plus 3x înmulțit cu 1 minus e înmulțirea

se face obișnuit ca și la numere

reale Înmulțind 4 cu fiecare număr

din a doua paranteză apoi înmulțim

numărul 3 cu fiecare număr din

a doua paranteză 4 ori 1 este patru

patru ori minus e este minus 4

e 3 ori 1 este trei in trei ori

minus e este minus 3 e pătrat egal

cu 4 minus 4y plus 3y Ela a doua

este minus unu iar minus 3 ori

minus 1 este plus 3 patru uși cu

3 este 7 iar minus 4x plus 3 e

este minus e în continuare vom

calcula modul din z unu ori doi

și avem modul din 7 minus e egal

cu radical din 7 la a doua plus

minus 1 la a doua egal cu radical

7 la a doua este 49 plus 15050

este 25 ori 2 și obținem în final

5 radical din 2 continuăm cu punctul

f trebuie să calculăm Suma de 1

la pătrat plus z 2 la pătrat mai

întâi calculez 1 la pătrat vom

avea 4 plus 3 totul la a doua egal

aici aplicăm formula de calcul

prescurtat a plus b totul la a

doua este egal cu a la a doua plus

doi a b plus b la a doua și vom

avea a 4 la a doua plus doi ori

4 ori 3 plus 3 la a doua egal cu

16 plus 24 3e la a doua este 9

e pătrat dar e pătrat este minus

unu așa dar voi scrie minus 9 egal

16 minus nu este 7 plus 24 e acum

să calculăm 10 2 la pătrat avem

1 minus e totul la a doua aici

aplicăm formula a minus b la a

doua este egal cu a la a doua minus

2ab plus b la a doua și avem unul

la a doua adică 1 minus 2x plus

e la pătrat egal cu 1 minus 2 la

a doua cum spuneam este minus 1

și obținem în final minus doi i

Deci 1 la pătrat plus z 2 la pătrat

va fi egal cu 7 plus 24 minus 2

egal cu 7 plus 22 e și ultimul

punct trebuie să calculăm raportul

Z 1 supra Z2 egal cu 4 plus 3 y

supra 1 minus i pentru a scrie

Acest număr sub forma algebrică

va trebui să amplificăm cu conjugata

numitorului conjugata va fi 1 plus

e și vom avea patru plus 3 pe lângă

1 plus y supra 1 minus e pe lângă

1 plus e egal 4 ori 1 este 4 plus

4x plus 3 plus 3 e pătrat supra

a minus b pe lângă a plus b este

a la a doua minus b la a doua Deci

vom avea 1 la a doua minus y la

a doua egal cu 4 plus 4 și cu 3

e este 7 e trei e la a doua va

fi egal cu minus 3 supra 1 minus

y la a doua este minus unu Deci

avem minus minus unu adică plus

1 egal 4 minus trei este 1 plus

7 supra 2 scrie maces număr sub

forma algebrică și vom avea 1 pe

2 plus 7 pe 2 x un alt exercițiu

Determinați x și y știind că 1

plus 3 înmulțit cu x plus 1 minus

2 înmulțit cu y este egal cu 4

minus i înainte de a rezolva acest

exercițiu trebuie mai întâi să

discutăm puțin despre egalitatea

a două numere complexe dacă avem

numărul complex Z 1 de formă a

1 plus b1e iar Z2 de forma A2 plus

b2e atunci aceste două numere complexe

a sunt egale Dacă și numai dacă

A1 este egal cu a 2 și b 1 este

egal cu b 2 cu alte cuvinte două

numere complexe scrise sub forma

algebrică sunt egale dacă atât

părțile reale cât și părțile imaginare

coincid avem aici o egalitate de

două numere complexe al doilea

număr Complex 4 minus i este scris

sub forma algebrică însă primul

număr complex nu este sub forma

algebrică va trebui mai întâi să

desfacem parantezele să separăm

partea reală de ceai imaginară

iar apoi vom pune condiția ca partea

reală a primului număr complex

să fie egală cu 4 iar partea imaginară

să fie egală cu minus 1 Așadar

mai întâi desface parantezele și

vom avea x plus 3 x y plus y minus

2y e egal cu 4 minus x plus y aceasta

va fi partea reală plus din acești

doi termeni o să îl dăm factor

comun pe și vom avea 3x minus 2y

înmulțit cu e egal cu 4 minus i

și acum vom pune condiția ca x

plus y să fie egal cu 4 iar partea

imaginară adică 3 x minus 2 y să

fie egal cu minus unu Așadar vom

obține un sistem de Două ecuații

cu două necunoscute prima ecuație

a sistemului va fi x plus y egal

4 a doua ecuație va fi 3x minus

2y egal cu minus 1 voi rezolva

si sistem prin metoda reducerii

înmulțim prima ecuație cu 2 vom

obține 2 x plus 2y egal cu 8 și

3x minus 2y egal cu minus 1 adunăm

Cele Două ecuații și avem cinci

X egal cu 7 obținem astfel x egal

cu 7 supra 5 înlocuim valoarea

lui x întruna din ecuații de exemplu

în prima a descriem o dată x plus

y egal cu 4 x este 7 supra 5 De

ce avem 7 pe 5 plus y egal cu 4

rezultă egal cu 4 minus 7 supra

5 y vei fi egal 20 minus 7 13 ce

supra 5 Așadar obținem x egal cu

7 pe 5 y egal cu 13 supra 5