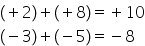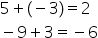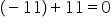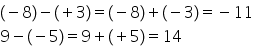Operaţii cu numere întregi: adunarea şi scăderea

în această lecție o să învățăm

adunarea și scăderea numerelor

întregi o să începem cu Adunarea

numerelor cu același semn am reprezentat

pe o axă câteva numere întregi

pentru a ușura calculele am fixat

sensul pozitiv și negativ indicat

de aceste două săgeți dacă avem

numere întregi pozitive ne deplasăm

de la origine spre dreapta iar

pentru numerele negative ne deplasăm

de la origine spre stânga și începem

cu acest exemplu plus 2 plus plus

5 ca să ne prezentăm pe axă numărul

plus 2 neam de plasat de la origine

două unități în sens pozitiv Iată

această săgeată roșie Indică numărul

plus 2 apoi în continuarea săgeți

roșii trebuie să mergem cinci unități

de măsură tot în sens pozitiv Iată

capătul săgeții albastre Indică

și Rezultatul acestui exercițiu

Așadar plus 2 adunat cu plus 5

ne dă plus 7 un alt exemplu să

adunăm plus trei plus plus trei

asa Reprezentăm numărul plus 3

mergem de la zero în sens pozitiv

trei unități de măsură iar Aici

este numărul plus 3 apoi în continuare

a săgeții roșii mergem încă trei

unități de măsură tot în sens pozitiv

iar finalul săgeții albastre Indică

și Rezultatul acestui exercițiu

prin urmare rezultatul calculului

este plus șase acum să vedem Cum

adunăm două numere negative și

avem aceste exemplu minus 2 plus

minus 4 ca să Reprezentăm numărul

minus 2 pe axa trebuie să ne deplasăm

de la origine în sens negativ două

unități de măsură iar Aici avem

numărul minus 2 apoi în continuare

a săgeții roșii trebuie să mergem

patru unități de măsură tot în

sens negativ Iată rezultatul la

care ajungem este minus 6 și încă

un exemplu minus unu adunat cu

minus 6 minus unu de la zero mergem

spre stânga o unitate de măsură

apoi în continuare a săgeții roșii

trebuie să mergem șase unități

de măsură tot spre stânga pentru

că avem minus 6 Iată ajungem la

numărul întreg minus șapte iar

acesta va fi și rezultatul exercițiului

acum să ne uităm puțin la aceste

sume și să încercăm să deducem

or Gula Generală de calcul observăm

mai întâi că semnul rezultatului

este semnul comun al celor doi

termeni Iată aici Am avut două

numere pozitive rezultatul a fost

număr pozitiv aici Am avut două

numere negative iar rezultatul

este negativ Acum putem să observăm

că modulul sumei este suma modulelor

celor doi termeni Dacă adunăm modulele

acestor numere Avem doi plus 5

egal cu 7 la fel și aici Dacă adunăm

modulele avem 2 plus 4 egal 6 și

normal sa reținem această regulă

pentru Adunarea numerelor care

au același semn Iată pentru a aduna

două numere întregi cu același

semn se adună modulele lor iar

rezultatul îl are semnul comun

Haideți acum să vedem Cum adunăm

numerele întregi cu semne diferite

a mai prezentat iarăși pe o axă

câteva numere întregi ca să ne

ușurăm calculele și pornim de la

acest exemplu plus cinci plus minus

doi trebuie să adunăm Așadar un

număr pozitiv cu un număr negativ

ca să ajungem la numărul plus cinci

ne deplasăm de la zero în sens

pozitiv cinci unități de măsură

Iată Aici este plus 5 acum pornim

de la acest număr trebuie să mergem

în sens opus adică în sens negativ

două unități de măsură capătul

săgeții albastre Indică și rezultatul

calculului Așadar plus 5 adunat

cu minus doi ne dă plus trei un

alt exemplu minus 6 adunat cu plus

4 ca să Reprezentăm numărul minus

șase mergem de la zero șase unități

în sens negativ Iată aici avem

minus 6 ca să adunăm acum la acest

număr numărul plus 4 pornind din

acest punct trebuie să ne deplasăm

patru unități de măsură dar în

sens pozitiv Iată numărul la care

am ajuns este minus doi acesta

va fi și rezultatul calculului

acum să ne uităm la aceste sume

și să încercăm să deducem iarăși

o regulă Generală de calcul pentru

Adunarea numerelor cu semne diferite

referitor la semnul rezultatului

putem observa că suma are semnul

numărului cu modulul mai mare dintre

numerele plus cinci și minus 2

cel cu modulul mai mare este plus

5 Așadar semnul rezultatului va

fi semnul acestui număr Deci plus

la fel și aici dintre numerele

minus 6 și plus 4 cel cu modulul

mai mare este minus 6 Așadar rezultatul

va avea semnul minus acum să vedem

cum se calculează modulul rezultatului

observăm că modulul acestei sume

este diferența modulelor celor

doi termeni pentru că 5 minus 2

ne dă 3 la fel și aici 6 minus

4 ne dă 2 în concluzie putem preciza

următoarea regulă pentru a aduna

două numere întregi cu semne diferite

se scad modulele lor iar suma va

avea semnul numărului cu modulul

mai mare trecem în continuare la

scăderea numerelor întregi Să presupunem

că avem aceste exercițiu 5 minus

trei și nu cunoaștem rezultatul

acestuia să notăm rezultatul cu

X scăderea este operația inversă

adunării Așadar x adunat cu 3 trebuie

să ne dea 5 Care este numărul care

adunat cu 3 ne dă cinci evidenta

acesta este 2 acum să luăm un alt

exemplu dacă avem minus 7 minus

plus 3 nu știm încă să efectuăm

scăderea numerelor întregi așa

că notăm Rezultatul acestui calcul

cu X dar x adunat cu numărul plus

trei trebuie să ne dea minus 7

după modelul anterior nu știm să

adunăm numerele întregi așa că

ne putem gândi Care este numărul

care adunat cu plus 3 să ne dea

minus 7 acesta este minus 10 pentru

că a minus 10 plus plus 3 ne dă

minus 7 Așadar Iată x este egal

cu minus 10 Deci rezultatul acestei

scăderi minus 7 minus plus 3 este

egal cu minus 10 însă minus 7 plus

minus 3 ne dă tot minus 10 pentru

că se adună modulele lor iar rezultatul

are semnul comun și atunci din

aceste două relații putem trage

concluzia că în minus 7 minus plus

3 este același lucru cu minus 7

adunat cu minus 3 dar numerele

plus trei și minus trei sunt numere

întregi opuse așa dar putem spune

că scăderea unui număr întreg este

echivalentă cu adunarea opusului

acelui număr și atunci să mai vedem

câteva exemple dacă avem plus 8

minus minus 6 trebuie să adunăm

la descăzut opusul scăzătorului

Deci o să avem plus 8 adunat cu

opusul numărului minus 6 deci cu

6 plus 8 și cu plus 6 este plus

14 un alt exemplu plus 9 minus

minus 3 procedăm la fel la descăzut

adică la numărul 9 adunăm opusul

scăzătorului 9 plus 3 este egal

cu 12 minus 6 minus plus 2 la descăzut

adunăm opusul numărului plus doi

Deci adunăm minus 2 minus 6 adunat

cu minus 2 minus 8 așa să reținem

că scăderea unui număr întreg este

echivalentă cu adunarea opusului

acelui număr o mică observație

aș vrea să mai facem dacă ne uitam

aici observăm că minus minus tot

transformat în plus Așadar întrun

exercițiu dacă vedem semnul minus

de două ori Putem să scriem direct

Plus în continuare mă faci un exercițiu

avem aceste exercițiu pentru care

o să redactezi rezolvarea în două

moduri plus 5 minus plus 7 plus

minus 11 minus minus 9 plus plus

3 scăderea numărului plus 7 înseamnă

adunarea opusul lui acestui număr

Așadar la numărul plus cinci trebuie

să adunăm opusul numărului plus

7 minus 7 îl copiem pe minus 11

aici avem meanness minus Putem

să scriem direct plus 9 și plus

3 egal Adunarea numerelor întregi

ca și Adunarea numerelor naturale

este asociativă comutativă iar

0 este element neutru din moment

ce adunarea este asociativă putem

să adunăm primii doi termeni următorii

doi termeni și la final să îl adunăm

pe 3 plus 5 adunat cu minus 7 este

minus 2 plus minus 11 adunat cu

9 este minus 2 Și mai trebuie să

îl adunăm pe 3 egal paranteza rotundă

este obligatorie atunci când avem

Două semne alăturate din acest

motiv la am pus pe minus doi între

o paranteză pentru că aici aveam

un plus în fața acestuia pe când

în cazul primului termen minus

doi nu aveam alt semn în fața lui

de aceea în această situație nu

este obligatorie paranteza Deci

rețineți că folosind paranteze

rotunde atunci când avem Două semne

alăturate asa nu confundăm semnul

operației cu semnul numărului întreg

acum Venus 2 adunat cu minus 2

ne dă minus 4 plus trei și obținem

rezultatul minus unu și acum o

altă variantă de a redacta Rezolvarea

acestui exercițiu pentru A simplifica

scrierea nu vă mai pune semnul

plus în fața numerelor întregi

și avem cinci minus 7 minus 11

putem să renunțăm și la acest plus

minus minus 9 este plus 9 și plus

3 egal acum Avem cinci minus șapte

noi trebuie să știm că cinci minute

7 înseamnă de fapt 5 adunat cu

minus 7 pentru că scăderea este

echivalentă cu adunarea opusul

lui 5 adunat cu minus 7 ne dă minus

2 apoi îmi copiem pe minus 11 și

aici putem să facem 9 plus 3 ne

dă 12 egal minus 2 minus 11 înseamnă

minus 2 adunat cu minus 11 iar

rezultatul este minus 13 plus 12

acum adunăm două numere cu semne

diferite scădem modulele lor iar

rezultatul îl are semnul numărului

cu modulul mai mare Deci minus