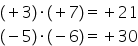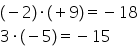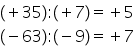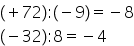Operaţii cu numere întregi: înmulţirea şi împărţirea
Tag-uri
Partajeaza in Google Classroom

Transcript
Înmulțirea și împărțirea numerelor
întregi o să încep cu înmulțirea
numerelor întregi cu semne diferite
să facem următoarea înmulțire minus
4 ori plus 3 Acest lucru se mai
poate scrie și minus patru ori
trei deoarece am spus în lecțiile
anterioare că nu este obligatoriu
să mai scriem Semnul plus h&n numerelor
naturale înmulțirea numerelor întregi
poate fi privită ca o adunare repetată
a aceluiași termen și atunci putem
scrie egal cu minus 4 plus minus
4 plus minus 4 care va fi egal
mai departe cu minus 12 am adunat
modulele lor iar la rezultat se
pune semnul comun și atunci putem
să tragem o concluzie un produs
de forma minus a ori plus b ma
fie egal cu minus aur b următorul
exercițiu să calculăm plus cinci
ori minus doi Acest lucru se mai
poate scrie și cinci ori A minus
2 înmulțirea numerelor întregi
este comutativă și atunci putem
scrie minus 2 ori 5 Care va fi
egal cu minus 2 adunat cu el însuși
de cinci ori dar această sumă va
fi egală cu minus 10 am adunat
valorile absolute iar la rezultat
se pune semnul comun și atunci
Putem să scriem că un produs de
forma plus a ori a minus b ma fie
egal cu minus a b observăm Așadar
că în cazul factorilor cu semne
diferite produsul va fi întotdeauna
un număr negativ Putem să scriem
această regulă produsul a două
numere întregi cu semne diferite
este negativ iar valoarea absolută
a produsului este egală cu produsul
valorilor absolute ale factorilor
continuăm cu împărțirea a două
numere întregi care au semne diferite
împărțirea este operația inversă
înmulțirii am văzut anterior că
minus 4 ori plus 3 este egal cu
minus 12 atunci făcând operația
inversă minus 12 împărțit la plus
3 va trebui să fie egal cu minus
4 atunci când împărțim două numere
cu semne diferite câtul va fi negativ
vom scrie și această regulă Dacă
împărțim două numere întregi cu
semne diferite câtul va fi negativ
iar valoarea absolută a câtului
este câtul valorilor absolute să
trecem acum la înmulțirea numerelor
întregi care au același semn o
să încep tot cu împărțire 18 împărțit
la minus 3 este egal cu minus 6
pentru că am văzut mai devreme
că dacă împărțim două numere de
semne diferite câtul este negativ
Haideți să facem proba acestei
împărțiri prin înmulțire dacă facem
proba obținem caninus 6 ori minus
3 este egal cu plus 18 adică cu
18 observăm Așadar că produsul
a doua numere negative este un
număr pozitiv în cazul în care
numerele sunt pozitive plus 6 ori
plus 3 lucrurile sunt foarte clare
deoarece numerele întregi pozitive
pot fi privite ca numere naturale
și atunci șase ori 3 va fi Evident
egal cu 18 Deci în ambele situații
Rezultatul este pozitiv putem trage
o concluzie un produs de formă
a minus a ori minus b mahidol cu
plus abur iar din a doua relație
putem spune că un produs de formă
a plus a ori plus b este egal cu
plus a b și atunci să scriem această
regulă produsul a două numere întregi
cu același semn este pozitiv iar
valoarea absolută a produsului
este produsul valorilor absolute
a factorilor continuăm cu împărțirea
a două numere întregi cu același
semn dacă Numerele sunt pozitive
de exemplu să facem plus 16 împărțit
la plus 2 gazul acesta Rezultatul
este plus 8 deoarece Privim numerele
întregi pozitive ca pe niște numere
naturale să vedem ce se întâmplă
dacă împărțim două numere întregi
negative dorim să facem împărțire
a minus 16 împărțit la minus doi
Acest rezultat nu îl cunoaștem
și o să îl notăm cu x dacă dorim
să facem proba prin înmulțire va
trebui ca x ori minus 2 să fie
egal cu minus 16 Care este numărul
întreg care înmulțit cu minus doi
Nevada minus 16 acel număr este
plus 8 De ce x este egal cu plus
8 deoarece plus 8 ori minus doi
este egal cu minus 16 Așadar rezultatul
acestei împărțiri este plus 8 o
să mai scrii o dată împărțirea
minus 16 împărțit la minus doi
este egal cu plus 8 sau mai simplu
cu 8 observăm că rezultatul împărțirii
a două numere întregi care au acelasi
semn este întotdeauna un număr
pozitiv și o să scriem și această
regulă Dacă împărțim două numere
întregi cu același semn câtul va
fi pozitiv iar valoarea absolută
a câtului este câtul valorilor
Absolute asa sintetizam Putem să
scriem următoarea regulă a semnelor
valabilă atât la înmulțirea cât
și la împărțirea numerelor întregi
atunci când trebuie să înmulțim
sau să împărțim două numere întregi
care au același semn și el pozitiv
sau negativ rezultatul va fi întotdeauna
un număr pozitiv iar dacă trebuie
să înmulțim sau să împărțim două
numere întregi având semne diferite
rezultatul va fi întotdeauna un
număr negativ ca și o generalizare
produsul a n numere întregi negative
este pozitiv Dacă n este par și
negativ Dacă n este impar de exemplu
Produsul a trei numere întregi
negative va fi negativ deoarece
3 este un număr impar iar produsul
a patru numere întregi negative
va fi pozitiv deoarece 4 este un
număr par dar o să vedem imediat
acest lucru făcând niște exerciții
un prim exercițiu minus șase ori
plus 8 minus ori plus este minus
6 ori 8 este 48 nu S9 ori minus
trei plus ori minus este minus
9 ori 3 este 27 minus 1 ori minus
2 minus ori minus este plus iar
unul ori doi este doi Putem să
scriem Mai simplu doi fără Semnul
plus al patrulea exemplu minus
6 ori 0 What is Ero deoarece Orice
număr întreg înmulțit cu 0 este
egal cu 0 punctul M plus 5 ori
5 deoarece trebuie să înmulțim
două numere pozitive rezultatul
va avea Semnul plus iar 5 ori 5
este 25 punctul f patru ori minus
6 Plus ori minus este minus iar
4 ori 6 este 24 minus 3 ori plus
4 ori minus 1 înmulțim mai întâi
primele două numere minus ori plus
este minus 3 ori 4 este 12 înmulțit
cu minus 1 minus ori minus este
Plus iar 12 ori 1 este 12 punctul
H minus 3 ori minus 5 ori minus
doi minus trei ori minus cinci
este plus 15 ori minus doi plus
ori minus este minus iar 15 ori
2 este 30 cum spuneam și mai devreme
Produsul a trei numere întregi
negative va fi un număr negativ
minus 2 ori plus 3 ori minus 4
ori plus 5 deoarece înmulțirea
este asociativă putem să înmulțim
primii doi factori și ultimii doi
minus ori plus este minus 2 ori
3 este 6 ori minus ori plus este
minus 4 ori 5 este 20 minus 6 ori
minus 20 este plus 120 să facem
acum și câteva împărțiri prima
împărțire minus 15 împărțit la
minus trei regula semnelor este
aceeași ca și la înmulțire minus
cu minus este plus iar 15 împărțit
la 3 este 5 o a doua împărțire
plus 30 împărțit la minus 6 plus
împărțit la minus este minus iar
30 împărțit la 6 este 5 și unul
din exemplu minus 16 împărțit la
2 minus împărțit la plus este minus
16 împărțit la 2 este 8 înmulțirea
numerelor întregi are aceleași
proprietăți ca și înmulțirea numerelor
naturale este comutativă asociativă
numărul unu este element neutru
și înmulțirea este distributivă
față de adunare și scădere