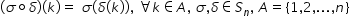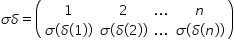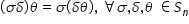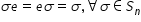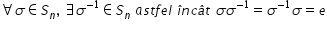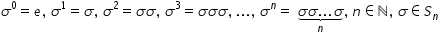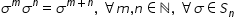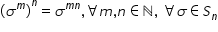Operații cu permutări

în acest videoclip vom studia operațiile

cu permutări de grade in și proprietățile

acestora pentru început să ne reamintim

câteva noțiuni necesare pentru

înțelegerea acestor operații respectiv

proprietăți de membre amintit cum

realizăm compunerea funcțiilor

Care sunt proprietățile compunerii

funcțiilor Ce înțelegem prin funcția

inversă și ce este o permutare

de grade dacă avem o funcției f

definită pe o mulțime A cu valori

în mulțimea b și o funcție G definită

pe mulțimea b cu valori în mulțimea

C compuse a funcției G cu funcția

f se notează așa și reprezintă

o funcție definită pe mulțimea

A cu valori în mulțimea cedată

prin relația G compus cu f de x

este egal cu c d e f de x pentru

orice x aparținând mulțimii A astfel

oricărui element din mulțimea A

A corespunde prin funcția f un

element un unic element în mulțimea

b iar fiecărui din mulțimea b e

corespunde prin funcției G 1 like

element din mulțimea C în concluzie

fiecărui element din mulțimea A

îi corespunde prin funcția G compus

cu 1 like element în mulțimea C

o primă proprietate a compunerii

funcțiilor este asociativitatea

astfel pentru oricare trei funcții

definite pe a cu valori în b g

definită pe d cu valori în c f

definită pe c cu valori în d e

f compus cu g totul compus cu a

c este egal cu e f compus cu rezultatul

compunerii lui Jack u h compunerea

funcțiilor ales un element neutru

astfel pentru orice funcției f

definită pe mulțimea A cu valori

în mulțimea b există funcția identică

1 a definită pe a cu valori în

A și funcția identică 1b definită

pe b cu valori în b astfel încât

f compus cu 1 a este egal cu EF

iar 1b compuse cu este egal tot

cu el atenție compunerea funcțiilor

nu este o operație comutativă a

funcției f definită pe mulțimea

A cu valori în mulțimea b este

inversabilă dacă există o altă

funcție G definită pe b cu valori

în a astfel încât e f compus cu

g să fie egal cu funcția identică

definită pe b iar G compus cu f

să fie funcție de Tică definită

pe mulțimea A această funcție G

nu este altceva decât inversă funcției

f ia se notează f la minus 1 dar

Atenție nu este egal cu 1 supra

o funcție este inversabilă dacă

și numai dacă ea este bijectivă

numim permutare de grad n o funcție

bijectivă definită pe mulțimea

A cu valori în mulțimea A unde

mulțimea A este mulțimea formată

din elementele 1 2 respectiv N

mulțimea tuturor permutărilor de

gradient se notează cu e Cindy

c n Fie mulțimea A formată din

elementele 1 2 3 respectiv N Sigma

și Delta două permutări de grade

Yan asta înseamnă că Sigma și Delta

sunt definite pe mulțimea A cu

valori în mulțimea a adică cele

două funcții au același domeniu

respectiv codomeniu ceea ce permite

compunerea lor rezultă astfel funcția

Sigma compus cu Delta definită

pe mulțimea A cu valori în mulțimea

A dar și tata compus cu Sigma definită

pe mulțimea A cu valori în mulțimea

A Sigma și Delta sunt permutări

așa dar sunt funcții bijective

compunerea a două funcții bijective

este tot o funcție bijectivă ceea

ce ne permite să concluzionăm că

rezultatul compunerii a doua permutări

de Gran este totul permutare de

grade Ianca Așadar Sigma cu Delta

dar și Delta compus cu Sigma aparțin

lui Sen compunerea a doua permutări

sau produsul a doua permutări Sigma

și Delta din Sen este tot o permutare

Deci Sigma compus cu Delta este

totul permutare de același grad

adică Sigma compus cu Delta este

definită pe mulțimea A cu valori

în mulțimea A și este dată de relația

Sigma compus cu Delta de ca este

egal cu Sigma de Delta de ca oricare

ar fi ca aparținând mulțimii A

Pentru a ușura scrierea utilizăm

în loc de Sigma compus cu Delta

Sigma ordered dacă permutarea Sigma

are reprezentarea 1 2 respectiv

N cu imaginile Sigma de 1 Sigma

de 2 respectiv Sigma de Ioan iar

permutarea Delta are reprezentarea

1 2 respectiv N cu imaginile Delta

de 1 Delta de 2 Delta dalyan Sigma

Delta este o permutare cu reprezentarea

1 2 respectiv N cu imaginile Sigma

de Delta de 1 Sigma de Delta de

2 respectiv Sigma de Delta de ea

Să considerăm acum Spre exemplu

două permutări Sigma și Delta din

S3 astfel Sigma are reprezentarea

unu doi trei cu imaginile doi unu

trei Delta are prezentarea unu

doi trei cu imaginile trei doi

unu Sigma ori Delta are reprezentarea

unu doi trei cu imaginile Sigma

de Delta de 1 Sigma de Delta de

2 Sigma de Delta de 3 adică permutarea

cu următoarele imagini cu Delta

de 1 Delta de 1 este 3 adică vom

avea Sigma de 3 Delta de doi pe

Delta de doi este tot doi Și atunci

vom obține Sigma de 2 iar lui 3

Delta de 3 pe Delta de 301 ceea

ce înseamnă că vom avea aici Sigma

de 1 adică obținem permutarea cu

reprezentarea 1 doi trei cu imaginile

syma de trei pe syma de 303 Deci

trei Sigma de 2 pe Sigma de 2 este

un Sima de unu sa ma de unu este

doi adică 2 Analog Delta compuse

cu Sigma are reprezentarea 1 doi

trei cu imaginile Delta de Sigma

de 1 Delta de Sigma de 2 Delta

D Sigma de 3 Adică permutarea 1

2 3 cu imaginile Sigma de 1 Sigma

de unu este doi Deci Delta de doi

Sigma de doi si ma de doi este

unul Deci Delta de 1 Sigma de 3

Sigma de 303 deci de alta de 3

Adică permutarea 1 2 3 cu imaginile

Delta de 2 Delta de 2 este 2 deci

pe Moni corespunde doi Delta de

1 pe Delta de 1 este trei deci

lui doi va corespunde trei Delta

de 3 Delta de 301 Deci lui trei

a corespunde 1 Observați cum permutarea

Sigma compus cu Delta este diferită

de Delta compus cu Sigma dacă urmărim

doar corespondențele pentru compunerea

permutări Sigma cu Delta putem

proceda astfel lui unui corespunde

trei lui 3 corespunde trei în consecință

lui unui va corespunde 3002 corespunde

doi doi doi corespunde 1 în consecință

lui 2 corespunde 1 2 3 a corespunde

unui unei corespunde doi astfel

lui 3 corespunde doi sau Dacă vom

calcula permutarea Delta ori Sigma

așezăm cele două permutări una

lângă cealaltă și urmărim corespondențele

adică unde corespunde doi lui 2

corespunde doi În consecință lui

unui corespunde doi doi doi corespunde

unului unui corespunde trei Așadar

lui 2 corespunde trei lui 3 corespunde

trei iar lui 3 corespunde 1 în

concluzie i3 corespunde 1 proprietățile

compunerii permutărilor de grade

in deriva din proprietățile compunerii

funcțiilor cu un compunerea funcțiilor

este o operație asociativă și compunerea

permutarilor este o operație asociativă

astfel oricare ar fi Sigma Delta

și teta aparținând lui isen Sigma

ori Delta totul înmulțit cu teta

este egal cu Sigma înmulțit cu

rezultatul produsului lui Delta

cute.com compunerea funcțiilor

admitere element neutru funcția

identică și compunerea permutărilor

admite element neutru permutarea

identică Așadar există permutarea

identică e aparține lui AC n astfel

încât pentru orice permutare Sigma

aparținând lui isen Sigma ori este

egal cu aur Sigma și este egal

cu Sigma permutările funcție bijective

în consecință inversabile astfel

oricare ar fi permutarea Sigma

aparținând lui Sen există Sigma

la minus unu aparținând lui n astfel

încât Sigma o Sigma la minus 1

este egal cu Sigma la minus 1 ori

Sigma și este egal cu AE ia de

Cum putem determina inversă pentru

o permutare Sigma de gradul I reprezentare

a acesteia este 1 2 en cu imaginile

Sigma de 1 Sigma de 2 segm Adrian

Sima la minus unu se construiește

astfel Sima de 1 Sigma de 2 Sigma

de n cu imaginile 1 2 en și ordonam

apoi linia întâi lunda cum o permutare

Sigma din S4 Sigma are următoarea

reprezentare 1 2 3 4 cu imaginile

3 1 4 2 Sigma la minus 1 are următoarea

reprezentare imaginile și le așezăm

pe prima linie 3 1 4 2 cu imaginile

1 2 3 4 Adică ordonând acum prima

linie 1 2 3 4 lui 1a corespunde

doi Deci doi lui e2e corespunde

patru deci patru trei Nico răspunde

1 iar lui 4-a corespunde 3 aceasta

este permutarea inversa sau putem

face și ordonarea în același timp

fii acum o permutare Sigma din

S5 Sigma are reprezentarea 1 2

3 4 5 cu imaginile 3 5 2 1 4 Sigma

la minus 1 o determină mustra 1

2 3 4 5 cu imaginile lui 1 și corespunde

4 lui 2-a corespunde trei lui trei

a corespunde unui paturi corespunde

5 iar lui 5 corespunde doi atenție

compunerea funcțiilor nu este o

operație comutativă în consecință

nici compunerea permutarilor nu

este operație comutativă fie Sigma

o permutare din Sen Considerăm

că Sigma la 0 este permutare identică

Sigma la un puterea unui este Sigma

Sigma la puterea a doua este Sima

o Sigma atunci de ducem că puterea

aiana apere mutării Sigma reprezintă

produsul permutări Sigma cu ea

însăși de n ori oricare ar fi n

un număr natural să vedem acum

Cum calculăm Produsul a două puteri

Sigma la m înmulțit cu Sigma la

n reprezintă Sigma înmulțit cu

Sigma de m ori înmulțit cu Sigma

înmulțit cu Sigma de n ori adică

avem m Factor înmulțit cu infectări

în total mplus în factori în concluzie

Sigma la puterea n plus deducem

așadar relația Sigma la m înmulțit

cu Sigma la n reprezintă Sigma

la puterea n plus n oricare ar

fi m și n numere naturale pentru

calculul lui Sigma la m totul la

puterea n scrie ma ceastă putere

ca Sigma la m înmulțit cu Sigma

la m de n ori obținem Sigma la

puterea M plus m plus m de n ori

și în final Sigma la puterea M

Orion am obținut următoarea formulă

Sigma la m totul la puterea n este

egal cu Sigma la puterea M ori

m oricare ar fi m și n numere naturale

în următorul videoclip vom vorbi

despre transpoziție imaginații

văd cum ar fi să Compuneți două

coduri Cezar să zicem cu pasul

2 respectiv cu pasul 3 ce credeți

că se întâmpla