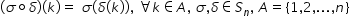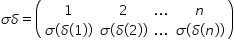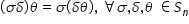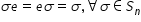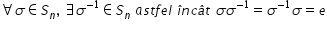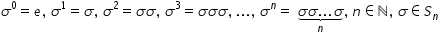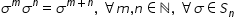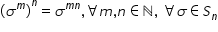Operații cu permutări- aplicații
Tag-uri
Partajeaza in Google Classroom

Transcript
pentru fixarea noțiunilor legate
de operațiile cu permutări de propunem
în acest videoclip rezolvarea urmatoarei
probleme dar de trei permutări
Sigma Delta teta de grad 4 dorim
să rezolvăm ecuațiile siegmeyer
x egal cu Delta x ori Sigma egal
cu Delta Sigma ori x ori Delta
egal cu teta să calculăm puterea
100 respectiv puterea 2017 apel
motorii Sigma și să determinăm
Cardinalul mulțimii m formată din
puterile lui Sigma să rezolvăm
Pentru început prima ecuație Sigma
ori x este egal cu Delta cu Mo
si permutare este inversabilă putem
înmulțit la stânga acestei egalități
cu inversa permutarii Sigma obținând
egalitatea Sigma la minus 1 War
Sigma ori x este egal cu Sigma
la minus 1 ori delta.com Simona
minus 1 ori Sigma era permutarea
identică avem egalitatea a X a
cu Sigma la minus 1 ori Delta dar
permutarea ei Era permutarea identică
adică elementul neutru pentru produsul
permutărilor x este egal cu Simon
la minus 1 ori Delta să înlocuim
acum pe Sigma la minus unu respectiv
pe Delta simbol la minus 1 este
permutarea 1 2 3 4 lui unui corespund
2 lui 2 corespunde 4 lui 3 corespunde
1 iar lui Patri corespunde trei
iar permutarea Delta este 1 2 3
4 1 3 4 2 produsul acestor două
permutări este permutarea 1 2 3
4 lui unui corespunde unui unui
corespunde doi pe doi corespunde
trei luni trei corespunde unui
3 corespunde 4 lui 4 corespunde
3004 corespunde doi iar lui doi
corespunde 4 pentru cea de ecuație
procedăm în mod similar pornind
de la ecuația x ori Sigma egal
cu Delta de data aceasta vom înmulțit
la dreapta cu permutarea inversă
a lui Sigma obținând egalitatea
x Sigma aur Sigma la minus 1 este
egal cu Delta ori Sigma la minus
unu permutarea Sigma Sigma la minus
1 este permutarea identică Așadar
x ori y egal cu Delta ori Sigma
la minus unu adică x este egal
cu Delta ori Sigma la minus unu
înlocuind obținem permutările 1
2 3 4 1 3 4 2 iar permutarea inversă
a lui Sigma 1 2 3 4 2 4 1 3 Rezultatul
este permutarea 1 2 3 4 lui unui
corespunde doi lui doi e corespunde
trei îi corespunde 4004a corespunde
doi lui 3 corespunde unului unui
corespunde unui ar lui Patri corespunde
trei iar trei ale corespondent
4 pentru cea de a treia ecuație
Sigma x ori Delta este egal cu
teta înmulțit la stânga cu Sigma
la minus 1 iar la dreapta cu Delta
la mine așa vom obține ecuația
Sigma la minus 1 ori Sigma ori
x ori Delta Delta la minus 1 este
egal cu Sigma la minus 1 ori Deta
ori Delta la minus unu Sigma la
minus 1 ori Sigma este părea identică
de al tau ori Delta la minus 1
este tot permutarea identică adică
e ori x ore e este egal cu saiba
la minus 1 ori teta ori Deltă la
minus unu adică x este egal cu
permutarea 2 3 4 2 4 1 3 ori permutare
atâta Adică permutarea 1 2 3 4
4 1 2 3 și 8 permutarea Delta la
minus 1 pe care o Vom calcula acum
1 2 3 4 luni corespunde 1 lui 2
corespunde 4 lui 3 corespunde doi
iar lui 4 corespunde trei obținem
permutarea 1 2 3 4 luni corespund
a11y corespunde 4 iar lui 4 corespunde
trei lui 2 corespunde 4 lui 4 corespunde
trei iar lui 3 corespunde unui
3 corespunde doi lui 2 corespunde
unui unui corespunde doi lui Patri
corespunde 3003 corespunde doi
iar lui 2 corespunde 4 ne propune
Cum să calculăm Sigma la puterea
100 respectiv Sigma la puterea
2017 să calculăm pentru început
câteva puteri ale lui Sigma și
anume suma la puterea a doua este
egal cu 1 2 3 4 3 1 4 2 1 2 3 4
3 1 4 2 Adică permutarea 1 2 3
4 lui unui corespund de trei luni
trei corespunde 4 lui 2 1 2 1 3
2 3 4 lui 4 2 lui 42 iar lui 2
1 Sigma la puterea a treia reprezintă
Sigma umana pătrat Adică permutarea
1 2 3 4 3 1 4 2 1 2 3 4 4 3 2 1
egal cu permutarea 1 2 3 4 lui
unui corespunde 4 lui 4 corespunde
2 plus 2 3 iar E34 lui 3 2 2 2
1 2 4 1 iar lui 1 3 Sigma la puterea
a patra reprezintă Sigma Sigma
la puterea a treia Adică permutarea
1 2 3 4 3 1 4 2 înmulțit cu permutarea
1 2 3 4 2 4 1 3 egal cu permutarea
1 2 3 4 1 corespunde 2 lui 2 corespund
a1224 lui 4 2 2 3 1 2 1 3 2 4 3
iar lui 3 4 observăm că am obținut
permutarea identică Așadar Simon
la puterea a cincea va fi Sigma
Sigma la a patra adică Sigma Sigma
la puterea a șasea va fi Sigma
Sigma la a cincea adică Sigma vor
Sigma Sigma pătrat Sigma la puterea
a șaptea va fi Sigma Sigma la a
șasea Sigma Sigma la pătrat Sigma
la puterea a treia iar ce ma la
opta este syma la a patra totul
la a doua adică este părea identică
observăm că puterile lui Sigma
se repetă din 4 în 4 Sigma la puterea
a patra este egal cu Sigma la puterea
a opta Sigma la puterea a 5-a este
egal cu Sigma Sigma la puterea
a șasea este egal cu Sigma la puterea
a doua Iar Sigma la puterea 7 este
egal cu suma la puterea a treia
pentru calculul lui Sigma la puterea
100 îl vom împărți pe 100 la 4
obținem câtul 25 Sigma la puterea
100 îl putem scrie astfel ca Sigma
la puterea a patra totul la puterea
25 adică permutarea identică la
puterea 25 adică permutarea identică
pentru calculului Sigma la puterea
2017 îl vom împărți pe 2017 la
4 obținem câtul 504 dar restul
unu pe syma la puterea 2017 îl
vom scrie ca Sigma la puterea 504
ori 4 plus 1 această putere o putem
scrie ca produsul a două puteri
cu baza Sigma adică Sigma la puterea
504 ori 4 ori Sigma la puterea
1 iar această putere o putem scrie
casima la a patra totul la puterea
a 504 o Sigma la puterea unu obținem
așa dar e ori Sigma adică Sigma
să determinăm acum Cardinalul mulțimii
m formată din elementele e Sigma
Sigma la pătrat Sigma la puterea
n fie Sigma la puterea n o permutare
care aparține acestei mulțimi n
este un număr natural conform teoremei
împărțirii cu rest pe an nu putem
scrie ca patru ori q plus iar deîmpărțitul
egal cu împărțitorul ori câtul
plus restul unde restul trebuie
să fie mai mic decât împărțitorul
adică mai mic decât 4 atunci Sigma
la puterea n poate fi scris astfel
Sigma la puterea 4 ori q plus iar
această permutare vom Scrie ca
produs ulei două permutări cu aceeași
bază adică Sigma la puterea 4 q
înmulțit cu Sigma la puterea aer
sau Sigma la puterea a patra totul
la puterea a q ori în Sigma la
puterea iar Dar ce ma la puterea
a patra în văzut că este permutarea
identică adică e la puterea q or
Sigma la puterea ieri adică Sigma
la puterea air.com aer este un
număr mai mic decât 4 L poate fi
unul din numerele 0 1 2 sau 3 în
concluzie Sigma la puterea a nu
poate fi decât mutarea identică
Sigma Sigma la puterea a 2-a respectiv
Sigma la puterea a treia am arătat
astfel că Sigma la puterea n nu
poate fi decât unul din cele patru
elemente permutare identică Sigma
Sigma la puterea a doua sau Sigma
la puterea a treia adică mulțimea
m este formată doar din 4 elemente
distincte permutarea identică Sigma
Sigma la a doua respectiv Sigma
la a treia obținând astfel cardinalul
acestei mulțimi M este egal cu
4