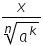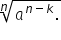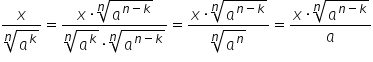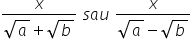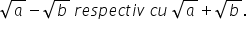Operații cu radicali. Raționalizarea numitorului (I)

în această lecție vom rezolva câteva

exerciții cu radicali și vom vorbi

și despre raționalizarea numitorului

primul exercițiu 7 radical de ordinul

3 din 16 minus 4 radical de ordinul

3 din 54 plus 2 radical de ordinul

3 din 250 pentru început vom încerca

să scoatem factorii de sub radical

și vom scrie 7 radical de ordinul

3 din 2 la a patra adică 2 la a

treia ori doi minus 4 radical de

ordinul 3 54 înseamnă 27 ori 2

adică 3 la a treia ori doi plus

doi 250 este 125 ori doi adică

5 la a treia ori 2 egal factorii

care au exponentul 3 vor ieși de

sub radical și vom scrie șapte

ori doi ori radical de ordinul

3 din 2 minus patru ori 3 ori radical

de ordinul 3 din 2 plus 2 ori 5

ori radical de ordinul 3 din 2

egal cu 14 radical de ordinul 3

din 2 minus 12 radical de ordinul

3 din 2 plus 10 radical de ordinul

3 din 2 14 minus 12 este 2 plus

10 egal 12 radical de ordinul 3

din 2 următorul exercițiu radical

de ordinul 6 din 3 radical din

3 la a treia ori 2 la a 11 ori

6 ori radical de ordinul 4 din

3 radical de ordinul 3 din 3 la

7 ori nouă pentru început vom introduce

acești factori sub radical acest

radical este de ordinul doi primari

atunci Când introducem factorul

3 sub radical exponentul acestuia

va fi 2 iar Aici avem radical de

ordinul 3 prin urmare nu mai avea

sub radical 3 la a treia scrie

radical de ordinul 6 din radical

din 3 la a doua ori 3 la a treia

ori 2 la a 11-a iar în loc de 6

m scrie 2 ori 3 ori radical de

ordinul 4 din radical de ordinul

3 așa cum spuneam aici vom avea

sub radical 3 la a treia ori 3

la a șaptea iar 9 este 3 la a doua

egal atunci când extrage un radical

din un alt radical trebuie să înmulțim

ordinele radicalilor aici avem

radical de ordinul 6 iar Aici avem

radical de ordinul doi în consecință

vom avea radical de ordinul 12

din 3 la puterea 2 plus 35 plus

unu șase Deci trei la șase ori

2 la 11 ori 2 face 2 la 12-a ori

aici la fel înmulțim indicii radicalilor

și obținem radical de ordinul 12

din 3 la puterea a 12-a 3 plus

7 10 plus 212 penal factorii care

au exponentul 12 vor ieși în fața

radicalului și Avem doi radical

de ordinul 12 din 3 la a șasea

ori 3 egal cu 6 radical de ordinul

12 din 3 la a șasea Acum putem

să simplificăm radicalul acesta

ordinul radicalului este multiplu

de 6 prin urmare simplificăm cu

șase și obținem șase radical de

ordinul doi din trei adică 6 radical

din 3 următorul exercițiu avem

cinci supra radical de ordinul

3 din 6 radical în general sunt

numere iraționale adică fracții

zecimale infinite neperiodice așa

dar Încercăm să evităm împărțirea

la un număr irațional iar pentru

aceasta vom folosi raționalizarea

numitorului Acesta este un procedeu

prin care transformăm numitorul

din număr irațional între număr

rațional pentru a elimina radicalul

de la numitor nu folosi următoarea

formulă radical de ordinul n din

a la n este egal cu radical de

ordinul n din a totul la n și egal

cu a Așadar pentru a elimina acest

radical va trebui ca sub radical

să avem 6 la a treia observăm că

șase înmulțit cu 6 la a doua ne

dă 6 la prin urmare vom amplifica

această fracție cu radical de ordinul

3 din 6 la a doua și obținem 5

radical de ordinul 3 din 6 la a

doua supra radical de ordinul 3

din șase înmulțit cu radical de

ordinul 3 din 6 la pătrat egal

cu 5 radical de ordinul 3 din 36

supra așa cum spuneam radical de

ordinul 3 din 6 la a treia egal

cu 5 radical de ordinul 3 din 36

supra 6 am reușit astfel să transformăm

numitorul dintre un număr irațional

într un număr rațional următorul

exercițiu avem 4 supra radical

din 7 minus radical din 3 pentru

a raționaliza numitorul aceste

fracții vom amplifica această fracție

cu conjugată expresiei de la numitor

mai exact nu folosi următoarea

formulă de calcul prescurtat a

minus b pe lângă a plus b este

egal cu a la pătrat minus de la

pătrat în cazul nostru a este radical

din 7 iar b este radical din 3

avem Așadar a minus b ca să obținem

radical din 7 la pătrat respectiv

radical din 3 la pătrat și astfel

să eliminăm radicalii va trebui

să amplificăm această fracție cu

cea de a doua paranteză adică cu

radical din 7 plus radical din

3 această expresie se numește conjugată

expresiei de la numitor obținem

astfel 4 pe lângă radical din 7

plus radical din 3 supra radical

din 7 minus radical din 3 pe lângă

radical din 7 plus radical din

3 egal cu 4 pe lângă radical din

7 plus radical din 3 supra radical

din 7 la pătrat minus radical din

3 la pătrat egal cu 4 pe lângă

radical din 7 plus radical din

3 supra 7 minus trei adică patru

simplificăm prin patru și obținem

în final radical din 7 plus radical

din 3 și ultimul exercițiu avem

opt supra 2 plus radical din 5

plus radical din 3 vom folosi aceeași

formulă ca și în exercițiul anterior

cu mențiunea că de data aceasta

a va fi 2 plus radical din 5 iar

b este radical din 3 conjugat aceste

expresii va fi 2 plus radical din

5 minus radical din 3 ca să se

vadă mai clar aplicarea formulei

de calcul prescurtat vom grupa

termenii astfel și avem 8 pe lângă

2 plus radical din 5 minus radical

din 3 aceasta este conjugat a supra

2 plus radical din 5 plus radical

din 3 înmulțit cu 2 plus radical

din 5 minus radical din 3 egal

cu 8 pe lângă 2 plus radical din

5 minus radical din 3 supra avem

A plus B A plus B pe lângă a minus

b adică a la a doua minus b la

a doua prin urmare obținem 2 plus

radical din 5 la pătrat minus radical

din 3 la pătrat egal cu 8 pe lângă

2 plus radical din 5 minus radical

din 3 supra aici folosim iarăși

o formulă de calcul prescurtat

învățat în clasele mai mici A plus

B totul la pătrat este a la pătrat

plus 2ab plus b la pătrat aici

folosim această formulă și avem

2 la a doua 4 plus 2ab adică 4

radical din 5 plus radical din

5 la pătrat adică 5 minus radical

din 3 la pătrat este 3 egal cu

8 pe lângă 2 plus radical din 5

minus radical din 3 supra 4 plus

5 9 minus 3 6 6 plus 4 radical

din 5 la numitor puteri se dă factor

comun pe 2 și avem opt pe lângă

2 plus radical din 5 minus radical

din 3 supra 2 pe lângă 3 plus 2

radical din 5 a cum simplificăm

cu 2 și ne rămâne 4 pe lângă 2

plus radical din 5 minus radical

din 3 supra 3 plus 2 radical din

5 va trebui să mai amplificăm o

dată cu conjugată expresiei de

la numitor de data aceasta conjugate

va fi 3 minus 2 radical din 5 Așadar

avem 4 pe lângă 2 plus radical

din 5 minus radical din 3 totul

pe lângă 3 minus 2 radical din

5 supra 3 plus 2 radical din 5

pe lângă 3 minus 2 radical din

5 egal 2 continuăm mai jos la numărător

Am putea să desfacem parantezele

poate se mai reduc niște termeni

avem 4 pe lângă 2 ori 3 6 minus

4 radical din 5 plus 3 radical

din 5 minus 2 ori 5 10 minus 3

radical din 3 și plus doi radical

din 15 supra a plus b pe lângă

a minus b este a la a doua adică

trei la a doua minus b la a doua

2 radical din 5 la pătrat egal

cu 4 pe lângă 6 minus 10 este minus

4 minus 4 radical din cinci cu

trei radical din cinci este minus

radical din 5 apoi minus 3 radical

din 3 copiem și plus 2 radical

din 15 totul supra 3 la a doua

este 9 iar 2 radical din 5 la pătrat

înseamnă patru ori 520 9020 este

minus 11 egal acest minus trece

la numărător și astfel se schimbă

semnele tuturor termenilor din

paranteză și voi scrie astfel 4

supra 11 pe lângă 4 plus radical

din 5 plus 3 radical din 3 minus

2 radical din 15 în clipul urmator

vom rezolva alte exerciții în care

avem la numitor radical de ordinul

3