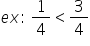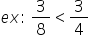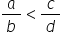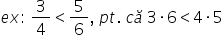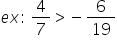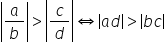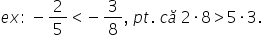Ordonarea numerelor raționale

în această lecție o să învățăm

să ordonam numerele raționale numerele

raționale pot fi scrise atât sub

formă de fracție ordinară cât și

sub formă de fracție zecimală mai

întâi învățăm să comparăm fracțiile

ordinare avem aici un întreg pe

care o să îl împart în patru părți

egale Dacă voi hașura o parte voi

obține fracția 1 supra 4 Ia Dacă

voi hașura două părți din acestea

bombe obține fracția 2 supra 4

având în vedere că două pătrimi

reprezintă o suprafață mai mare

decât o pătrime opt spune că fracția

2 supra 4 este mai mare decât fracția

1 supra 4 Să împărțim acum acest

întreg în opt părți egale Dacă

voi faci urat două părți dintre

acestea obținem fracția 2 supra

8 să comparăm acum fracția 2 supra

8 cu 2 supra 4 ne uităm la porțiunea

hașurată cu galben și la cea hașurată

cu albastru având numele că porțiunea

albastră este mai mare decât cea

galbenă de ducem că fracția 2 supra

4 este mai mare decât fracția 2

supra 8 putem constata Așadar următoarele

aspecte dintre două fracții pozitive

care au același numitor a fi mai

mare cea cu numărătorul mai mare

iar dintre două fracții pozitive

care au același numărător este

mai mare cea cu numitorul mai mic

îmi scrie aceste reguli dintre

două fracții pozitive care au același

numitor este mai mare cea cu numărătorul

mai mare și putem să dăm exemplul

pe care îl am văzut mai devreme

unul supra 4 este mai mică decât

fracția 2 supra 4 ia dintre două

fracții pozitive care au același

numărător este mai mare cea cu

numitorul mai mic am văzut că fracția

2 supra 8 este mai mică decât fracția

2 supra 4 în cazul în care trebuie

să comparăm două fracții pozitive

care nu au nici același numitor

și nici același numărător o variantă

posibilă ar fi să aducem fractiile

la același numitor și să aplicăm

prima regulă sau o altă variantă

ar fi să înmulțim pe diagonală

fracția a supra b va fi mai mică

decât fracția c supra d Dacă a

ori b este mai mic decât b orice

să vedem un exemplu dorim să comparăm

fracțiile 3 supra 4 și 5 supra

6 o să înmulțim pe diagonală trei

ore 6 și 4 x 5 36 este 18 iar 4520

având în vedere că 18 este mai

mic decât 20 1 scrie că fracția

3 supra 4 este mai mic decât fracția

5 supra 6 dintre două fracții cu

semne diferite este mai mare fracția

pozitivă întotdeauna un număr rațional

pozitiv va fi mai mare decât un

număr rațional negativ de exemplu

4 supra 9 va fi mai mare decât

minus 6 supra 13 Regula numărul

5 dacă avem fracțiile negative

a supra b și c supra D atunci a

supra b este mai mică decât c supra

d dacă valoarea absolută a fracția

a supra b este mai mare decât valoarea

absolută a fracției c supra D adică

modul de aur d este mai mare decât

modul din b orice să luăm un exemplu

dorim să comparăm fracțiile negative

minus 2 supra 5 și minus 3 supra

8 mai întâi vom compara modulele

acestor două fracții și anume Compară

fracțiile pozitive 2 supra 5 și

3 supra 8 după regula amintită

mai devreme înmulțim pe diagonală

2 ori 8 este 16 iar 3 ori 5 este

15 având în vedere că 2 ori 8 este

mai mare decât 5 ori 3 înseamnă

că fracția 2 supra 5 este mai mare

decât fracția 3 supra 8 dar revenind

la fractiile inițiale Care erau

numere negative mo inversa acest

semn pentru că fracția a minus

2 supra 5 este mai mică decât minus

3 supra 8 în general dintre două

numere raționale negative este

mai mare cel cu modulul mai mic

de exemplu numărul minus 3 este

mai mare decât minus 4 pentru că

modulul numărului minus 3 este mai

mic decât modulul numărului minus

4 dintre două numere raționale diferite

este mai mare cel care pe o axă

a numerelor este reprezentat la

dreapta celuilalt De exemplu fracția

1 supra 2 este mai mică decât 2

dacă ai factum împărțirea observăm

că 1 supra 2 se poate transforma

fracție zecimală și obținem 0 reprezentând

pe axa numerele raționale 1 supra

2 și 2 observăm că 2 este situată

la dreapta numărului 1 supra 2

Așadar 2 este mai mare decât 1 supra

2 în general pentru a compara două

numere raționale scrise sub formă

diferită adică un număr scris sub

formă de fracție ordinară și celălalt

sub formă de fracție zecimală este

bine să dea ducem la aceeași formă

ori transformăm ambele numere fracție

zecimală ori transformăm în fracție

ordinară să facem acum un exercițiu

Scrieți în ordine crescătoare numerele

minus 2 plus 4 minus 6 5 5 42 supra

5 și minus 15 supra 2 avem aici

niște numere raționale scrise atât

sub formă de fracție zecimală cât

și sub formă de fracție ordinară

voi transforma ultimele două fracții

ordinare în fracții zecimale făcând

împărțirea 42 împărțit la cinci

cinci în 42 se cuprinde de 8 ori

5 ori 840 efectuăm scăderea punem

virgulă adăugăm 05 în 20 intră

de 4 ori 5 x 420 Așadar 42 supra

5 este egal cu 8 15 împărțit la

2 doi în 15 se cuprinde de șapte

ori șapte ori 2 este 14 punem virgulă

adăugăm un zero doi în 10 intră

de cinci ori 5 ori 2 este 10 minus

15 supra 2 este egal cu minus 7

și acum să scriem aceste numere

în ordine crescătoare numerele

negative vor fi mai mici decât

cele pozitive așa dar trebuie să

începem cu cele negative avem trei

numere negative minus 7 minus 2 și

minus șase dintre acestea cel mai

mic la fix al cu modulul mai mare

și anume minus 7 Deci primul număr

în ordine crescătoare este minus

15 supra 2 următorul în mod negativ

mai mare decât minus 7 este minus

6 urmează apoi minus 2 am terminat

cu numerele negative urmează cele

pozitive avem patru numere pozitive

plus 4 5 5 și 8 Este clar că cel mai

mic este 4 și cel mai mare 8 să vedem

între aceste două numere care va

fi cel mai mare comparăm fracțiile

zecimale 5 și 5 cinci virgulă perioada

2 este o fracție zecimală infinită

aceasta este egală cu 5 2 și așa

mai departe cifra 2 se repete la

nesfârșit iar 5 înseamnă de fapt

5 să ne uităm acum la aceste două

fracții zecimale partea lor întreagă

este egală 5 este egal cu 5 comparăm

acum prima zecimală observăm că

și aceasta coincide 2 este egal

cu 2 trecem la a doua zecimală

și observăm că 2 este mai mare

decât 0 și atunci putem trage concluzia

că 5 este mai mare decât 5 era acum

să revenim la ordinea crescătoare

urmează cum spuneam 4 apoi 5 urmează

cinci virgulă perioadă 2 și mai

avem 8 adică fracția 42 supra 5

aceasta este ordinea crescătoare

a numerelor în continuare o să

discutăm despre partea întreagă

și partea fracționară a unui număr

rațional prin definiție partea

întreagă a unui număr rațional

x notată cu paranteză dreaptă este

cel mai mare număr întreg mai mic

sau egal cu x de exemplu partea

întreagă a numărului 2 este egală

cu 2 pentru că 2 este cel mai mare

număr întreg dar mai mic decât

2 în alte exemplu partea întreagă

a numărului minus 2 este minus 3

pentru că minus trei este cel mai

mare număr întreg dar mai mic decât

minus 2 Dacă ne imaginăm aceste

numere reprezentate pe o axă minus

3 este situat la stânga lui minus

2 Deci minus 3 este mai mic decât

minus 2 acum definim partea fracționară

a unui număr rațional x aceasta

se notează cu paranteză acoladă

și ea este diferența dintre numărul

x și partea sa întreagă de exemplu

partea fracționară a numărului

este diferența dintre numărul 2

și partea întreagă a lui 2 egal

în continuare cu 2 minus partea

întreagă este 2 și obținem 0 partea

fracționară a numărului minus 2

este egală cu minus 2 minus partea

întreagă a numărului minus 2 egal

cu minus 2 minus partea întreagă

a lui minus 2 este minus 3 egal

cu minus 2 plus 3 și egal cu 0