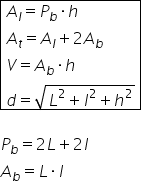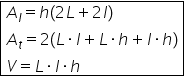Paralelipipedul dreptunghic (aplicații)

îmi faci acum două aplicații cu

paralelipipedul dreptunghic în

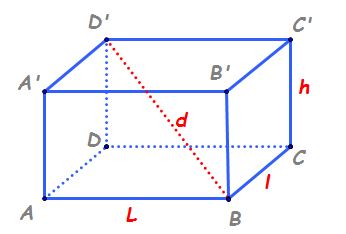
prima problemă Mi se dă un paralelipiped

dreptunghic cu dimensiunile de

8 cm 6 și 12 cm Să calculăm aria

laterală aria totală volumul și

lungimea diagonalei pentru a determina

mai întâi aria laterală Haideți

să trecem aici că avem lungime

lățime și înălțime și vom trece

și dimensiunile date 8 cm așa în

paranteză 6 cm și 12 cm Aria laterală

formula ariei laterale este egală

cu perimetrul bazei ori înălțimea

asta înseamnă că aria laterală

chiar Haide să trecem aici aria

laterală Cu cât este egală Păi

avem perimetrul bazei adică 2 pe

lângă lungime plus lățime înmulțită

cu înălțimea vom avea 2 pe lângă

avem 8 plus 6 Iată 8 plus 6 înmulțit

cu înălțimea care are 12 cm vom

avea doi ori 14 ori 1228 ori 12

în livada 336 centimetri pătrați

ca să calculăm acum aria totală

avem suma dintre aria laterală

și de două ori aria bazei Cu cât

este egala aria bazei avem lungime

ori lățime pentru că baza este

dreptunghi adică 8 ore 6 48 de

cm pătrați din aceste două relații

obținem că aria totală Cu cât este

egal avem aria laterală adică 336

adunat cu Deci avem aici plus de

două ori aria bazei adică 2 înmulțit

cu 48 facem această înmulțire apoi

facem suma cu 336 și vom obține

432 de cm pătrați să calculăm acum

volumul avem produsul celor trei

dimensiuni adică lungime ori lățime

ori în schimb a alte cuvinte rezultă

că volumul este egal cu opt ori

6 ore 12 facem acest calcul și

obținem 576 de cm cubi să calculăm

acum și lungimea să trecem formula

Diagonala este egală cu radical

din ce vom trece sub radical avem

aici L la a doua l mare la a doua

plus amic la a doua plus H la a

doua Deci rezultă că sau Haide

să scriem în continuare egal cum

vom avea radical din avem opt la

pătrat adunat cu 6 la pătrat adunat

cu 12 la pătrat și vom obține aici

Cum avea 64 adunat cu 36 adunat

cu 144 trebuie să facem această

sumă de sub radical avem aici 100

cu 144 de 244 și trebuie să trecem

și radicalul radical din 244 după

ce descompunem în factori acest

număr vom obține că diagonala Nevada

doi radical din 61 de centimetri

următoarea problemă Se dă paralelipipedul

dreptunghic a b c d a prim b prim

c prim D prim cu ab egal 4 centimetri

lungimea diagonalei este de 10

cm și măsura unghiului făcut de

o diagonală cu planul bazei ABC

este de 60 de grade Să găsim aria

laterală și volumul acum lungimea

unei diagonale este de 10 cm Știind

că toate diagonalele sunt congruente

Deci construim aici diagonala exemplu

de prim b care are lungimea de

10 cm mai știm că măsura unghiului

făcut de o diagonală cu planul

bazei ABC este de 60 de grade toate

diagonalele fac cu planul bazei

a b c d unghiuri care au aceeași

măsură asta înseamnă că toate au

măsura de 60 de grade de ce unghiul

făcut de diagonala D prim b cu

planul a b c d este de 60 de grade

Ce înțelegem prin unghiul unei

drepte cu un plan este unghiul

făcut de dreapta respectivă cu

proiecția a Pe plan care e proiecția

lui d prim b Pe planul a b c d

foarte simplu punctul B aparține

planului înseamnă că proiecția

punctului b este chiar punctul

b d prim d perpendicular pe AC

n asta înseamnă că proiecția punctului

e d prim pe plane sta punctul d

Deci proiecția segmentului d prim

b Pe planul a b c d este d b Ce

înțelegem prin acest lucru că măsura

unghiului făcut de D prim b cu

d b adică unghiul D prim BD Acesta

are 60 de grade bun și acum haide

să scriem ce am discutat până acum

și anume vom trece pe scurt că

proiecția Pe planul abc A diagonalei

D prim b este d b d c măsura unghiului

D prim b d d prim b d este de 60

de grade ca să determinăm acum

aria laterală și volum De ce avem

nevoie îmi trebuie să găsim dimensiunile

acestui paralelipiped Deci avem

nevoie și de lățime și de înălțime

Cum putem să găsim de exemplu înălțimea

apoi foarte simplu pentru că triunghiul

d prim d b este un triunghi dreptunghic

avem aici un unghi de 90 de grade

asta înseamnă că în acest triunghi

putem să aplicăm formule trigonometrice

Deci nu vă mai scrie că de prim

D perpendiculară pe acest plan

de baie inclusă în plan asta înseamnă

că d prim D perpendiculară pe d

f și trecem direct că măsura unghiului

D prim d b d prim d b este de 90

de grade și atunci putem să aplicăm

formule trigonometrice în acest

triunghi rezultă să aplicăm mai

întâi formula sinusului pentru

ca astfel am găsit lungimea segmentului

d prim d iar sinus să scriem ceva

mai jos deci sinus de unghiul b

Cu cât este egal în uităm pe figură

cateta opusă unghiului B adică

D prim d d prim D supra lungimea

ipotenuzei adică D prim d d prim

b de unde rezultă că avem sinus

de 60 de grade sinus de 60 de grade

ne dă de prim d d prim D supra

D prim b care are 10 cm Cât este

sinus de 60 de grade pâine de radical

din 3 pe 2 De ce avem că radical

din 3 supra 2 egal cu d prim D

supra 10 rezultă că d prim de cu

cât va fi egal cu 10 ori radical

din 3 pe 2 adică 5 radical din

3 si venim mai ieși trecem cinci

ori radical din 3 pe 2 si ma acum

pe DB fi Aplicând teorema lui Pitagora

În triunghiul d prim d b Fie putem

să aplicăm formula cosinusului

cosinus de unghiul b cosinus de

B este egal cu trece în formula

lungimea catetei alăturate unghiului

trecut aici Deci d b supra lungimea

ipotenuzei de primul b rezultă

cosinus de 60 de grade este egal

cu d b ceea ce Vrem să aflăm de

prin B are 10 cm Cât este Costin

de 60 de grade 1 pe 2 egal cu d

b supra 10 de unde rezultă că d

b are 10 cm Sigur nu era singura

variantă pentru că acest unghi

are 30 de grade și puteam să folosim

în triunghiul d prim DB teoremă

unghiului de 30 de grade asta înseamnă

că DB este jumătate din lungimea

ipotenuzei adică jumătate din 10

Deci are 5 cm un parfum nights

at trebuie să scriem că avem 10

supra 2 adică 5 cm și am găsit

că DB are 5 cm am găsit avem înălțimea

avem lungimea ne mai trebuie lățimea

adică lungimea segmentului a d

cum o determină foarte simplu avem

aici un triunghi dreptunghic măsura

unghiului A are 90 de grade deci

putem să trecem aici și fie aplicăm

la nu arată bine deloc Deci avem

aici Unul de 90 de grade și fie

aplicăm teorema lui Pitagora În

triunghiul d a d fie putem să folosim

numerele pitagoreice astfel Avem

așa triunghiul d ab cu măsura unghiului

A de 90 de grade mai știm că ipotenuza

de Be are 5 cm AB o catetă are

4 cm asta înseamnă că Lungimea

celeilalte catete este de 3 cm

Deci rezultă că Ade are 3 cm Pentru

că numerele 3 4 și 5 sunt numere

sau cum a spus aplicăm teorema

lui Pitagora și găsim că avem aici

3 cm avem toate dimensiunile să

calculăm aria laterală Deci șterge

tot ce am scris aici aria laterală

este egală cu perimetrul bazei

ori înălțimea Deci aria laterală

va fi egală cu perimetrul bazei

avem 2 pe lângă el mare plus l

mic înlocuim 2 înmulțit cu lungimea

este 4 lățimea este 3 Deci patru

plus trei ori înălțimea Care este

5 radical din 3 și vom avea așa

șapte ori 535 ori 270 radical din

3 centimetri pătrați și se află

am și volumul aria totală Nu ni

se cere să găsim și volumul aria

bazei ori înălțimea sau altfel

spus pentru un paralelipiped dreptunghic

am spus că trecem direct în lungime

ori lățime ori înălțime Deci volumul

este egal cu 4 ori 3 Deci avem

aici 4 mulți tcu trei înmulțiri

cu înălțimea adică 5 radical din

3 și avem patru ori 5 ne dă 20

ori 360 cu radicali din 3060 radical

din 3 centimetri cubi ce se încheiat