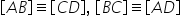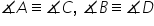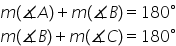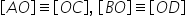Paralelogramul (Teorie)
Tag-uri
Partajeaza in Google Classroom

Transcript
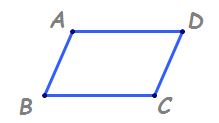
prin definiție un patrulater cu
laturile opuse paralele se numește
paralelogram observăm că latura
a d este paralelă cu bc și AB este
paralelă cu De ce să vedem care
sunt proprietățile paralelogramului
prima proprietate Laturile opuse
sunt congruente ab va fi congruentă
cu cd iar latura bc va fi congruentă
cu ad Cum putem să demonstrăm această
proprietate o se duce o diagonală
de exemplu ace observăm că stau
format două triunghiuri Triunghiul
abc și triunghiul adc aceste două
triunghiuri sunt congruente deoarece
au următoarele elemente congruente
având în vedere că a d este paralelă
cu bc și ac este secantă atunci
unghiul A1 va fi congruent cu unghiul
c 1 vinde unghiuri alterne interne
Dacă AB este paralelă cu d c iar
a c este secantă unghiul A2 va
fi congruent cu unghiul C doi fiind
de asemenea unghiuri alterne interne
cele două triunghiuri mai au o
latură comună aceasta este latura
AC va rezulta sunt cazului de congruență
unghi latura unghi că cele două
triunghiuri sunt congruente de
ce elementele corespondente vor
fi congruente latura ab va fi congruentă
cu cd iar latura bc va fi congruentă
cu ad congruență acestor două triunghiuri
implică și congruența unghiurilor
b și d aceasta este cea de a doua
proprietate a paralelogramului
unghiurile opuse sunt congruente
Deci unghiul b este congruent cu
unghiul d iar dacă am 2 Să demonstrăm
că unghiul A este congruent cu
unghiul c atunci m duce diagonala
bd sar forma alte două triunghiuri
ia din congruența celor triunghiuri
va rezulta că unghiul A este congruent
cu unghiul c cea de a treia proprietate
a unui paralelogram unghiurile
alăturate sunt suplementare de
exemplu măsura unghiului A plus
măsura unghiului b este egală cu
180 de grade Acest lucru se datorează
faptului că dreptele AD și BC sunt
paralele iar a b fiind o secantă
unghiul A și unghiul b sunt unghiuri
interne de aceeași parte a secantei
Ați învățat în clasa a șasea că
unghiurile interne de aceeași parte
a secantei sunt suplementare Dacă
prelungim latura bc unghiul a va
fie congruent cu acest unghi pe
care îi putem nota cu x pentru
că sunt unghiuri alterne interne
dar unghiul x împreună cu unghiul
b formează un unghi cu măsura de
180 de grade înseamnă că și unghiul
a împreună cu unghiul b sunt suplementare
o altă proprietate a acestui paralelogram
diagonalele se înjumătățesc De
exemplu dacă îl construim diagonalele
ele se intersectează în punct o
atunci AO va fi congruent cu o
c iar b o va fi congruent cu OD
pentru a demonstra această proprietate
se demonstrează congruența triunghiurilor
aob și d o c a b e este paralelă
cu cd iar AC secantă rezultă că
unghiul b a o este congruent cu
unghiul o c d Dacă AB și CD sunt
paralele și Considerăm o altă secantă
b d atunci unghiul o d c va fi
congruent cu unghiul oba fiind
alterne interne a b este congruentă
cu DC pentru că am văzut la prima
proprietate că laturile opuse sunt
congruente și atunci conform cazului
de congruență umblatul unghi va
rezulta că cele două triunghiuri
sunt congruente Iar asta înseamnă
că și segmentele AO și oc vor fi
congruente respectiv b o și o d
rețineți aceste Patru proprietăți
ale paralelogramului pentru a demonstra
ca un patrulater este paralelogram
putem fi să aplicăm definiția adică
Să arătăm că are laturile opuse
paralele două câte două fie aplicăm
una din aceste patru proprietăți
însă mai este și o altă modalitate
de a demonstra ca un patrulater
este paralelogram dacă arătăm de
exemplu ca Acesta are două laturi
opuse paralele și congruente de
exemplu dacă arătăm că a d și b
c sunt paralele și congruente atunci
va rezultat că patrulaterul respectiv
este paralelogram și nu mai e nevoie
să demonstrăm congruența celorlalte
două laturi respectiv relația de
paralelism dintre acestea Haideți
să vedem această teoremă un patrulater
este paralelogram Dacă și numai
dacă are două laturi opuse paralele
și congruente observăm că această
teoremă conține expresia Dacă și
numai dacă înseamnă că această
teoremă este formată din alte două
teoreme teoremă directă și teoremă
reciprocă sârma directă sau implicația
directă este următoarea Dacă un
patrulater este paralelogram atunci
are două laturi opuse paralele
și congruente nu mai e nevoie să
demonstrăm această implicație deoarece
rezultă clar din definiția paralelogramului
și din prima proprietate pe care
am văzut o anterior iar teorema
reciprocă sau implicația inversă
este următoarea Dacă un patrulater
are două laturi opuse paralele
și congruente El este paralelogram
Demonstrați asa implicație inversă
am scris ipoteza și concluzia avem
un patrulater a b c d d a m dată
nu știind că este paralelogram
ne propunem să demonstrăm acest
lucru în patrulaterul a b c d Se
știe că a d este paralelă cu bc
și congruentă cu bc trebuie să
arătăm că a b c d este un paralelogram
și voi folosi definiția paralelogramului
arăta că și celelalte două laturi
a b și b c sunt paralele pentru
aceasta voi construit diagonala
AC Dacă Considerăm dreptele a b
și b c împreună cu secanta a ce
se formează o pereche de unghiuri
alterne interne acestea sunt unghiurile
BAC De ce a Dacă arăt că aceste
două unghiuri alterne interne sunt
și congruente va rezulta că ab
este paralelă cu d c pentru a demonstra
congruență acestor două unghiuri
încadrăm în două triunghiuri voi
arăta că triunghiul ABC este congruent
cu triunghiul c d a iar din congruența
celor două triunghiuri rezultat
și congruența unghiurilor respective
demonstrație Fiind date dreptele
AB și DC iar AC secantă ma rezultat
că unghiul bac împreună cu unghiul
de ce a formează o pereche de unghiuri
alterne interne în continuare vom
arăta că aceste unghiuri sunt congruente
Și atunci vom demonstra că ab este
paralelă cu bc comparăm triunghiul
abc cu triunghiul c d a știm din
ipoteza că b c este congruentă
cu a d mai știm din datele problemei
că a d este paralelă cu bc Dacă
Considerăm secanta AC se formează
două unghiuri alterne interne acestea
sunt unghiurile BCA și de aceea
Rescrie că unghiul BCA este congruent
cu unghiul dac sind unghiuri alterne
interne și observăm că aceste triunghiuri
au o latură comună aceasta este
latura AC segmentul AC este congruent
cu segmentul AC fiind o latură
comună din aceste trei relații
ma rezulta conform cazului de congruență
latura unghi latura a triunghiul
ABC este congruent cu triunghiul
c d a iar din congruență acestor
triunghiuri rezultă și congruența
unghiurilor bac și DCA ia raspuns
și eu unghiuri alterne interne
A rezultat că dreptele a b și b
c sunt paralele notez aceste relații
cu 1 și 2 din unu și doi va rezulta
că ab este paralelă cu bc Așadar
a b c d este un paralelogram

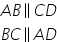
.JPG)