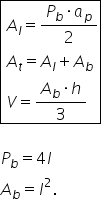Piramida patrulateră regulată (formule)

să vedem ce formule avem pentru

piramida patrulateră regulată și

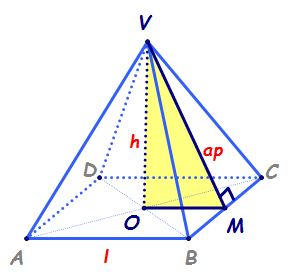
avem aici o asemenea piramidă reamintim

că bază este pătrat deci a b c

d este pătrat muchiile laterale

sunt congruente V a v b v c și

v d sunt congruente asta înseamnă

că fețele laterale Ce sunt sunt

triunghiuri isoscele congruente

și avem patru asemenea triunghiuri

Iată vab vbc vdc și v de a reamintim

că în o piramidă patrulateră regulată

înălțimea este segmentul care unește

vârful piramidei cu centrul cercului

circumscris bazei și centrul cercului

circumscris bazei se află un pătrat

la intersecția diagonalelor și

acum să vedem care este formula

pentru aria laterală știind că

trebuie să adunăm ariile fețelor

laterale Cum fețele laterale sunt

patru triunghiuri isoscele nota

că aria laterală este 4 înmulțit

cu aria unui triunghi isoscel toate

sunt congruente deci de exemplu

aria triunghiului vbc Acum putem

să aflăm aria acestui triunghi

ducând înălțimea din a pe BC și

să alegem alta culoare construim

mai întâi mijlocul segmentului

BC BM si va reprezenta este mediană

în triunghiul ebc însă cum vorbim

de un triunghi isoscel de bază

BC înseamnă că vm este și înălțime

de ce avem aici 90 de grade cu

alte cu aria triunghiului vbc Cu

cât este egală avem lungimea bazei

BC înmulțită cu lungimea înălțimii

corespunzătoare lui BC Deci ori

vm care atenție este apotema piramidei

deci putem să trecem aici ca avem

apotema piramidei Deci ori apotema

piramidei supra 2 și acum putem

să înlocuim în loc de aria triunghiului

v b c d aici vom trece acest raport

și rezultă că aria laterală este

egală cu 4 înmulțit cu linie de

fracție b c ori apotema piramidei

supra 2 absolut același lucru Am

făcut și când am găsit formula

pentru aria laterală a piramidei

triunghiulare regulate acum dacă

înmulțim pe 4 cu bc ce vom obține

Păi de ce este lungimea laturii

pătratului dacă înmulțim de patru

ori dacă adunăm de fapt de patru

ori această lungime ce obținem

pom obține perimetrul bazei Deci

notăm că aria laterală este egală

cu avem aici perimetrul bazei ori

apotema piramidei supra 2 și iată

că am găsit prima formulă aria

totală deja în sigură că știți

aria laterală a adunat cu aria

bazei Cât este aria bazei pe foarte

simplu pentru că baza este un pătrat

Deci dacă notăm cu l latura pătratului

atunci aria bazei este egală cu

el la pătrat și volumul piramidei

e deja al știind aria bazei înălțimea

supra 3D să nu te c supra 2 supra

3 înălțimea este reprezentată de

vreo De ce avem aici trecem Hai

ca un exercițiu foarte simplu Haide

să determinăm acum și lungimea

apotemei bazei sau mai bine zis

să exprimăm apotema bazei în funcție

de ce avem deja pe figură În primul

rând Care este apotema bazei este

distanța de la centrul cercului

circumscris bazei la o muchia bazei

de exemplu dacă ducem perpendiculară

din o pe BC si vom obține Păi obținem

chiar acest segment om și reamintim

pe scurt de ce obținem acest segment

om adică de ce om este apotema

bazei pentru că Iată punctul m

este mijlocul segmentului BC punctul

o este mijlocul segmentului a c

atunci ce reprezintă om în triunghiul

a c b o n este linie mijlocie asta

înseamnă că om este paralelă cu

AB de vreme ce a b perpendiculară

pe bc înseamnă că și om este perpendiculară

pe BC deci putem să trecem aici

că apotema piramidei apotema bazei

pardon este o m Care este lungimea

segmentului o m Păi de vreme ce

am spus că om e este linie mijlocie

în triunghiul ACB înseamnă că lungimea

segmentului o m este egală cu jumătate

din lungimea segmentului AB Deci

avem aici egal cu ab supra 2 adică

egal cu el pe 2 și din aceste două

relații putem să trecem aici că

rezultă a o temă bazei adică om

este egală cu el pe doi Deci apotema

bazei este egală cu jumătate din

lungimea muchiei bazei acestea

sunt formulele pentru piramida

patrulateră regulată avem aici

formula pentru aria laterală formula

pentru aria totală o formulă foarte

ușor de reținut și formula pentru

determinarea volumului de fapt

toate aceste trei formule pe care

le am încadrat sunt identice cu

formulele pe care le am de dus

pentru piramida triunghiulară regulată