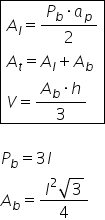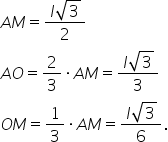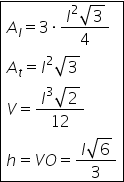Piramida triunghiulară regulată (formule)

să vedem acum Care sunt formulele

pentru piramida triunghiulară regulată

însă înainte Haideți să ne amintim

câteva proprietăți specifice ale

piramidei triunghiulare regulate

și anume baza este triunghi echilateral

muchiile laterale va vb și BC sunt

congruente în o piramidă triunghiulară

regulată înălțimea este segmentul

care unește vârful piramidei cu

centrul cercului circumscris bazei

Iată pentru că vorbim aici de un

triunghi echilateral abc este triunghi

echilateral atunci centrul cercului

circumscris coincide cu centrul

de greutate cu ortocentrul și cu

punctul de intersecție al bisectoarelor

pentru că medianele coincid cu

mediatoarele cu înălțimile și cu

bisectoare Ce înțelegem prin arie

laterală aria laterală de de fapt

suma ariilor fețelor laterale și

noi ca fețe laterale avem trei

triunghiuri V a b v b c și v a

c Cum sunt aceste triunghiuri Păi

sunt triunghiuri isoscele atenție

congruente Iată triunghiul V a

b c este congruent cu triunghiul

fbc Păi avem va congruent cu b

c b b este Latura comună a b congruent

cu b c d din cazul latură latura

laturilor semne că aceste două

triunghiuri sunt congruente cu

alte cuvinte fețele laterale sunt

reprezentate de triunghiuri isoscele

congruente Deci aria laterală se

poate scrie 3 înmulțit cu aria

unui triunghi Să considerăm aria

triunghiului v b c și acum ca să

determinăm această formulă Trebuie

să găsim aria triunghiului ales

de noi v b c știind că aria unui

triunghi este egală cu semi produsul

dintre lungimea unei laturi și

înălțimea corespunzătoare laturii

respective dacă alegem latura bc

Trebuie să ducem înălțimea din

b pe BC și mai întâi alegem m mijlocul

acestui segment BMC este vei m

este mediană în triunghiul jardin

v m este mediană în triunghiul

ebc însă cu un triunghiul este

isoscel cu baza BC înseamnă că

avem aici un unghi de 90 de grade

Deci vm este perpendiculară pe

BC și putem să notăm formula pentru

aria triunghiului v b c este b

c ori vm care reprezintă atenție

apotema piramidei supra 2 Și acum

înlocuim Deci rezultă că aria laterală

Cu cât este egală Păi avem Trei

înmulțit cu aria triunghiului ABC

adică ce avem aici trecem bc înmulțit

cu apotema piramidei supra 2 pe

3 în putem scrie aici 3 supra unu

și dacă înmulțim pe 3 cu bc si

vom obține trei ori b c iar o să

fac așa ne va da De fapt perimetrul

triunghiului ABC pentru că avem

un triunghi echilateral ab congruent

cu BC congruent și cu ei Ce înseamnă

că formula pentru aria laterală

este 3 ori b ce am spus că înseamnă

perimetrul bazei perimetrul bazei

înmulțit cu apotema piramidei supra

2 aceasta e formula pentru aria

laterală aria totală Păi e foarte

simplu trebuie să adunăm aria laterală

cu aria bazei Deci avem aria laterală

plus aria bazei Care este aria

bazei avem un triunghi echilateral

dacă Considerăm că notăm latura

muchia bazei cu l mic atunci ce

vom avea aria unui triunghi echilateral

cu latura notată aici L mic este

ermila doua radical din 3 supra

4 volumul unei piramide triunghiulare

regulate este dat de raportul aria

bazei ori înălțimea supra 3 și

înălțimea e reprezentată aici de

v acestea sunt formulele pentru

pere Da triunghiulară regulată

deci putem să încadrăm că avem

aici aria laterală perimetrul bazei

ori apotema piramidei supra 2 aria

totală foarte ușor de ținut minte

această formulă adunăm aria laterală

cu aria bazei aria bazei este aria

unui triunghi echilateral și formula

pentru determinarea volumului avem

aria bazei ori înălțimea supra

3 acum ca un exercițiu să determinăm

lungimea apotemei bazei în această

piramidă Ce înțelegem prin apotema

bazei apotema bazei este distanța

de la centrul cercului circumscris

bazei adică de la punctul o la

o muchia bazei pe atunci cum putem

să construim distanța de la punctul

o la latura bc ca să găsim această

apotema ba Păi a m Ce reprezintă

de vreme Ce e M este mijlocul segmentului

b c a m este mediană în triunghiul

ABC care atenție este triunghi

echilateral a dacă a m este mediană

înseamnă că a m este și înălțime

Deci avem ai Sper să se vadă un

unghi de 90 de grade Deci o să

trec că a m e perpendiculară pe

b c în punctele a o și m sunt coliniare

înseamnă că o m este perpendiculară

pe BC cu alte cuvinte distanța

de la o la BC este om Deci voi

trece aici chiar o să scriem direct

că apotema bazei notată a indice

b este om cum determinăm acum lungimea

segmentului o m Păi Punctul o este

centrul cercului circumscris bazei

însă triunghiul este echilateral

Ce înseamnă asta că punctul O coincide

cu centrul de greutate Deci triunghiul

abc este echilateral înseamnă că

punctul O egal cu punctul G unde

G este centrul de greutate Păi

atunci ce putem spune despre centrul

de greutate că el se află la două

treimi față de vârf și o treime

față de bază înseamnă că segmentul

o m are lungimea egală cu o treime

din lungimea medianei a m 1 supra

3 înmulțit cu Im aceste lucruri

deja au fost discutate când se

vorbit despre mediană depre medianele

unui triunghi și atunci ca să determinăm

lungimea segmentului om avem nevoie

de lungimea segmentului a m Ce

este a m este înălțime în triunghi

echilateral Deci triunghiul a b

c este echilateral a m este perpendiculară

pe BC asta înseamnă că a m este

înălțime deci a m Cu cât este egal

am notat latura triunghiului cu

l mic avem formula pentru înălțimea

unui triunghi echilateral al mic

radical din 3 pe 2 și din aceste

două relații Ce rezultă îi vom

înlocui om este egal cu 1 supra

3 înmulțit cu îl Înlocuim pe a

m în loc de aer trecem ce avem

aici linie de fracție al ori radical

din 3 supra 2 și facem calculul

avem Alo radical din 3 și la numitor

3 ori 2 adică 6 cu alte cuvinte

apotema bazei se scrie l radical

din 3 pe 6 și astfel am obținut

și formula pentru determinarea

apotemei bazei unei piramide triunghiulare

regulate