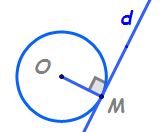
Poziţia unei drepte faţă de un cerc.

în această lecție o să vorbim despre

poziții relative ale unei drepte

față de un cerc există trei cazuri

posibile de poziționare a unei

drepte față de un cerc în funcție

de numărul de puncte de intersecție

dintre dreapta și cerc o prima

situație O dreaptă care nu are

niciun punct comun cu un cerc se

numește dreaptă exterioară cercului

în această figură observăm că dreapta

a intersectată cu cercul de centru

O și raza R este mulțimea vidă

pentru că dreapta A nu are niciun

punct comun cu Cercul o a doua

posibilitate este cea în care o

dreaptă are două puncte comune

cu Cercul iar în acest caz se va

numi dreaptă secantă față de cerc

observăm că dreapta b intersectează

cercul în două puncte a și b în

acest caz un spune că dreapta b

se numește secantă dreapta b intersectează

cercul de centru o și rază r în

punctele a și b și o adreia posibilitate

O dreaptă care are un singur punct

comun cu un cerc se numește dreaptă

tangentă la cerc observăm că dreapta

c intersectează cercul între un

singur punct pe care la mutat cute

acest punct se mai numește punct

de tangență dreapta c intersectată

cu cercul de centru O și raza R

este mulțimea formată din punctul

t acest punct a se mai numește

punct de tangență în continuare

o să vedem o teorema referitoare

la tangenta dusă la un cerc tangenta

este perpendiculară pe raza în

punctul de tangență cu alte cuvinte

Dacă dreapta d este o tangentă

la cerc iar o a este rază atunci

dreapta d este perpendiculară pe

dreapta o a m Demonstrați asta

teoremă folosind metoda reducerii

la absurd presupunem că dreapta

d nu este perpendiculară pe dreapta

o A înseamnă că putem să construim

noi această perpendiculară dusă

din punctul o pe dreapta d de exemplu

aceasta este perpendiculara din

A pe dreapta d pe care o să o notezi

cu om aici avem un unghi drept

și mai facem o construcție ajutătoare

o să fixez un alt punct pe dreapta

d punctul n astfel încât segmentul

m n să aibă aceeași lungime cu

segmentul a m cu alte cuvinte punctul

n este simetricul punctului a față

de m și unim punctele o și n Dacă

o A nu este perpendiculară pe D

înseamnă că putem să construim

noi această perpendiculară și e

om perpendiculară pe dreapta d

și a fixat un punct n pe dreapta

d astfel încât MN să fie egal cu

a m aici sau format Două triunghiuri

dreptunghice triunghiul a o m și

triunghiul n o m acestea sunt dreptunghice

în punctul m și vom arăta că ele

sunt congruente observăm că om

este o catetă comună a celor două

triunghiuri dar să scriem ca om

este congruent cu om fiind o latură

comună și segmentele a m și a n

m sunt congruente din construcția

pe care am făcut o a m este congruent

cu n m din construcție Observă

Master că cele două triunghiuri

au două catete respectiv congruente

și atunci va rezulta că ele sunt

triunghiuri congruente conform

cazului catetă catetă triunghiul

a o m este congruent cu triunghiul

n o m dar congruență a celor două

triunghiuri implică și congruența

ipotenuze lor acestora astfel o

n va fi congruentă cu o a rezultă

o a congruent cu o n dar o a este

o rază și atunci va rezulta implicit

că și o n ar trebui să fie rază

pentru că cele două segmente sunt

congruente dacă o a este egal cu

o n și egal cu raza cercului Atunci

înseamnă că punctul n ar trebui

să fie situat pe cerc pentru că

raza sa definit ca fiind segmentul

care unește centrul cercului cu

un punct situat pe cerc din urmare

punctul n ar trebui să aparțină

atât dreptei D cât și cercului

din această relație rezultă că

dreapta d ar intersectat cercul

de centru o și rază r în două puncte

în A și n n Dar acest lucru este

o contradicție cu faptul că dreapta

d este tangență la cerc pentru

că tangenta intersectează cercul

în un singur punct am ajuns astfel

la o contradicție și atunci presupunerea

pe care a făcut un ou este falsă

va rezultată presupunerea făcută

este falsă iar în consecință va

rezulta că tangenta este perpendiculară

pe raza Deci o a este perpendiculară

pe dreapta d rețineți această teoremă

tangenta la un cerc este întotdeauna

perpendiculară pe raza în punctul

de tangență continuăm cu o teoremă

dintre un punct exterior unui cerc

se pot duce două tangențe la acest

cerc avem punctul M exterior cercului

prin punctul m putem să construim

doar două tangentei la cercul de

centru O acestea sunt m a și m

b și în continuare să facem o aplicație

Demonstrați că tangentele duse

din punct exterior la cerc sunt

congruente trebuie să arătăm că

m a este congruentă cu m d pentru

aceasta o să unesc punctele o și

m observăm astfel că sa format

Două triunghiuri dreptunghice și

vom demonstra ca aceste două triunghiuri

sunt congruente având în vedere

că sunt triunghiuri dreptunghice

este suficient să găsim două elemente

respectiv congruente în afară de

unghiurile drepte observăm că o

a și o b sunt raze ale acestui

cerc de cele vor fi segmente congruente

o A este congruent cu OB pentru

că sunt raze cele două triunghiuri

au o latură comună aceasta este

om om este congruent cu om fiind

o latură comună om este ipotenuza

în fiecare dintre cele două triunghiuri

și atunci va rezulta că triunghiul

a o m este congruent cu triunghiul

b o m o f în cazului de congruență

ipotenuză catetă această relație

de congruență dintre cele două

triunghiuri implică și congruența

segmentelor a m și bem rezultă

că a m este congruent cu BM am

arătat astfel că tangentele duse

dintre un punct exterior la cerc

sunt congruente congruență acestor

două triunghiuri implică congruență

a tuturor elementelor omoloage

astfel putem să remarcăm că unghiul

b m o va fie congruent cu unghiul

a m o și unghiul b o m va fi congruent

cu unghiul a o m cu alte cuvinte

putem să afirmăm că dreapta m o

este bisectoarea unghiului a m

b și dreapta OM este bisectoarea

unghiului aob și în continuare

o să mai vedem o definiție un triunghi

se numește circumscris unui cerc

dacă laturile sale sunt tangentei

la cerc triunghiul ABC este circumscris

cercului de centru o pentru că

laturile sale sunt tangentei la

cerc observăm că latura ab a triunghiului

intersectează cercul în punctul

P Deci punctul p este punctul de

tangență apoi latură a c intersectează

cercul în punctul m și latura AC

intersectează cercul în punctul

n astfel dreptele o m o n și o

p vor fi raze în acest cerc iar

dreptele pe care le am desenat

punctat cu mov vor fi bisectoarele

unghiurilor a b și c dacă ne uităm

de exemplu la punctul C din punctul

c am dus tangentele ce an și cm

și atunci dreapta c o va fi bisectoarea

unghiului n c m apoi la fel dreapta

a o va fi bisectoarea unghiului

pe a n și dreapta b o va fi bisectoarea

unghiului P b m În consecință centrul

cercului înscris în triunghiul

ABC este chiar punctul de intersecție

al bisectoarelor unghiurilor triunghiului

iar triunghiul ABC se numește triunghi

circumscris cercului de centru

O