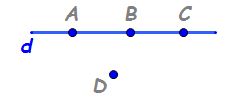
Poziţia unui punct faţă de o dreaptă

Fiind dată o dreaptă d și un punct

întâlnim două situații posibile

fie punctul a aparține dreptei

d și punctul nu aparține dreptei

în această figură observăm că punctele

a b și c sunt situate pe dreapta

d iar punctul d nu aparține dreptei

d având în vedere că punctele a

b și c aparțin aceleiași drepte

d l i se vor numi puncte coliniare

iar trei puncte care nu sunt situate

pe aceeași dreaptă se numesc puncte

necoliniare de exemplu punctele

a b și d fie necoliniare și definiție

a trei sau mai multe puncte care

aparțin aceleiași drepte se numesc

puncte coliniare fiind dat un punct

A prin acest punct vor trece o

infinitate de drepte aceasta este

una dintre ele a doua și tot așa

putem construi o infinitate de

drepte însă având două puncte distincte

prin aceste două puncte a și b

putem duce o singură dreaptă aceasta

va fi și axiomă dreptei o acționăm

este o propoziție matematică care

exprimă un adevăr acceptat fără

demonstrație în continuare o să

facem două exerciții primul exercițiu

stabiliți valoarea de adevăr a

propozițiilor de mai jos această

figură și trebuie să vedem dacă

aceste enunțuri sunt adevărate

sau false punctul a mare aparține

dreptei a mic Aceasta este o propoziție

adevărată punctul A mare nu aparține

dreptei b Aceasta este o propoziție

falsă deoarece punctul a aparține

atât dreptei a mică și dreptei

b observăm că punctul A este chiar

punctul de intersecție al dreptelor

a și b în acest caz punctul A o

să aparțină atât dreptei A cât

și dreptei b propoziția a nu aparține

dreptei b este o propoziție falsă

deoarece punctul a aparține dreptei

b punctul M aparține dreptei b

Aceasta este o propoziție falsă

observăm că punctul M nu este situat

nici pe dreapta a și nici pe dreapta

b punctul c aparține dreptei a

observat că punctul C este situat

pe dreapta b Deci propoziția c

aparține dreptei a este o propoziție

falsă punctul f aparține dreptei

b Aceasta este o propoziție adevărată

punctul B aparține dreptei a și

Aceasta este o poziție adevărată

punctul de nu aparține dreptei

a din nou este o propoziție adevărată

pentru că punctul d aparține dreptei

b și al doilea exercițiu Dați exemple

de puncte coliniare avem pe această

figură geometrică trei drepte dreapta

a dreapta b și dreapta c Trebuie

să găsim trei sau mai multe puncte

care aparțin aceleiași drepte observăm

că punctele m n și a aparțin dreptei

a mic în acest caz ele se vor lumi

puncte coliniare punctul p aparține

dreptei a punctul M aparține dreptei

a n aparține dreptei A și punctul

a mare aparține dreptei a în acest

caz un spune că aceste patru puncte

se numesc puncte coliniare t m

n și a sunt puncte coliniare să

dăm un alt exemplu de puncte coliniare

pe dreapta ce avem trei puncte

m s și q și acestea sunt puncte

coliniare M aparține dreptei c

s aparține dreptei c și punctul

q aparține dreptei c ma rezultat

că punctele m s și q sunt puncte

coliniare să ne uităm acum și la

dreapta b pe această dreaptă sunt

situate patru puncte p q o și a

Observați că punctul a aparține

atât dreptei b cât și dreptei a

pentru că punctul A este punctul

de intersecție a celor două drepte

punctul p aparține dreptei b punctul

Q aparține dreptei b punctul q

este punctul de intersecție al

dreptelor b și c înseamnă că el

va fi situat atât pe dreapta b

cât și pe dreapta c punctul O aparține

dreptei b și punctul a aparține

dreptei b îmi spuneai că punctele

p q o și a sunt puncte coliniare