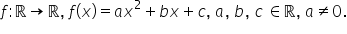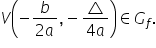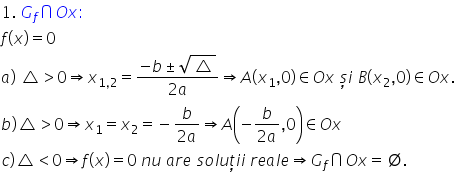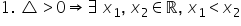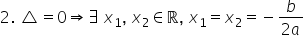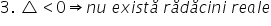Poziții relative ale graficului funcției și semnul funcției

în această lecție vom face Funcția

de gradul al doilea și mai clar

discuții teoretice și aplicative

preliminarii semnului respectiv

tabelului de variație corespunzător

funcției de gradul al doilea așa

cum am arătat în lecția precedentă

Funcția de gradul al doilea are

dreptul reprezentare grafică o

parabolă astfel că pentru o funcție

f definită pe r cu valori in R

cu f de x egal cu x pătrat plus

bx plus si cu foarte importanta

diferite zero reprezentarea grafică

este o parabolă un aspect important

aspect ce trebuie lămurit este

acela că reprezentare a funcției

de gradul al doilea adica parabolei

corespunzătoare se face în funcție

de semnul variabilei a a coeficientului

pătrat Da astfel că semnul variației

se poate afla în situația în care

este pozitiv De ce are plus și

atunci parabola corespunzătoare

va fi reprezentată în acest mod

atunci când ai este negativ parabola

corespunzătoare este reprezentată

în acest mod mai clar pentru a

verifica sau a demonstra corectitudinea

celor exprimate aici Da se pot

da două exemple de funcții în care

coeficientul a diferit de 0 prima

etapă pozitiv respectiv negativ

astfel că e f definită pe r cu

valori in R cu f de x egal cu x

pătrat înțelepte aici ca e unu

și atunci este pozitiv b și c sunt

egale cu 0 al doilea exemplu e

f definit pe r cu valori in R cu

f de x egal cu minus x pătrat înțelegând

de aici ca este minus unu Deci

este negativ sunt pe situația a

doua da cu b respectiv c egal exemplul

1 cel în care a este pozitiv a

fost discutat în lecția precedentă

drept pentru care pentru o lămurire

sau ca să ne aducem aminte despre

ce este vorba vă indic și vă recomand

să vă uitați la lecția precedentă

exemplul 2 este cel pe care vom

discuta în lecția prezent astfel

că am pensia f definită pe r cu

valori in R cu f de x egal cu minus

x pătrat pentru care ca și În exemplul

1 tot în lecția precedentă voi

da valorii 0 1 minus 1 2 minus

2 3 minus 3 în care să calculezi

funcție a este 0 este minus 0 la

pătrat înțelegând din aceasta că

e de zero zero și obțin punctul

de coordonate 0 0 Notați pe mine

cu o f de 1 egal cu minus 1 la

pătrat înțeleg din a e asta că

e de unde va fi egal cu minus unu

Deci punctul de coordonate 1 minus

1 ieftin minus 1 minus minus 1

la pătrat știind că orice număr

la pătrat cu ce valoare la pătrat

indiferent desen are plus dar cu

minusul din față va avea drept

rezultat tot minus astfel că obțin

punctul de coordonate minus 1 minus

1 notate cu b exact același principiu

este 2 f de minus doi este 300

minus 3 reprezentarea grafică este

cea pe care o vizualizam ai deci

x o y cu pe axa x avem valorile

1 2 3 respectiv minus 1 minus 2

minus 1 pentru x egal cu unu am

obținut minus 1 și atunci am unitate

coordonate 1 minus 1 pentru x egal

cu minus unu am obținut minus 1

și atunci b de coordonate minus

1 minus pentru punctul x egal cu

2 am obținut valoarea ministru

Și atunci ce ne de coordonate 2

și minus 4 respectiv minus 2x 8

sunt aceeași valoare minus 40 și

70 D de coordonate minus 2 minus

4 respectiv punctele 3 rest și

minus 3 cu x egal cu 3 se obține

minus 9 deci a de coordonate 3

și 5 și 9 pentru x egal cu minus

trei este coordonate minus trei

și pentru lămurirea situației vor

să vă aducă în această lecție și

reprezentarea grafică prezentată

în lecția precedentă cea pentru

funcția f definit pe r cu valori

in R cu f de x egal cu x pătrat

care așa cum o aduceți aminte sau

cum puteți vizualiza aici și în

lecția precedentă avea reprize

aceasta grafică Ce înțelegem în

acest moment pe baza celor două

exemple afirmăm în mod clar și

concret că atunci când aude este

pozitiv parabola funcției asociată

funcției de gradul al doilea este

convexă o sarcină foarte de tine

apă Da așa cum se vede de la x

pătrat ținea Turnu aici sus dar

umple cu apă Deci ține apă atunci

când ai este negativ parabola asociată

funcției de gradul al doilea este

concavă sau afirmăm la fel de des

nu ține apăsat pe același principiu

Dacă aș turnat apă așa de aici

de Sus parcurge pe lângă parabolă

fără ca parabola să țină apa Deci

ăsta e motivul pentru care afirmă

nu vine apă în continuare în condițiile

în care Funcția de gradul al doilea

are reprezentare diferită pe situațiile

a pozitiv respectiv se impun discuții

specifice fiecărei situații este

situația unui situația în care

a este pozitiv funcția f definită

pe r cu valori în l f de x egal

cu x pătrat plus bx plus c q ecuația

de gradul al doilea corespunzătoare

ax pătrat plus bx plus c egal cu

0 se poate afla în următoarele

trei situații teoretice spune pentru

că acestea teoretice fiu au fost

discutate în lecția care se discuta

despre ecuații de gradul al doilea

Sper că situația ei teoretică Delta

este negativ situația b teoretică

Delta este egal cu 0 respectiv

situații acetică Delta este pozitiv

în cazul în care Delta este negativ

ecuația nu are soluții reale atunci

când Delta egal cu 0 ecuația avea

două soluții reale dar regale confundate

spuneam noi atunci când Delta este

pozitiv ecuații are două soluții

distincte real si traducerea acestei

aspectele teoretice și anume dacă

ecuația nu are soluții reale parabola

corespunzătoare funcții nu atinge

sau nu intersectează axa o x a

sau x trebuie să fi interpretată

de fapt ca sarea la soluțiilor

ecuației de gradul al doilea cea

pe care se reprezintă sigur pe

care le obții după rezolvarea ecuației

de gradul al doilea astfel că situația

pe cea în care vorbim de soluții

reale egale sau confundate atrage

de că parabola corespunzătoare

funcției de gradul al doilea intersectează

axa o x întru un singur punct în

acel punct Numiți soluția ecuației

de gradul al 2 a treia și ultima

situație este aceea în care are

două soluții distincte Deci parabola

corespunzătoare funcția axei o

x în două puncte distincte cele

două puncte distincte fiind în

realitate X1 și X2 obținut din

rezolvarea ecuației de gradul 2

astfel o concluzie clară cu care

am putea să o so tragem în urma

discuției avut este aceea că pentru

pozitiv funcția f definită pe r

cu valori in R cu f de x egal cu

x pătrat plus bx plus ce va fi

comentată discutată în trei mari

situații Delta negativ Delta egal

cu 0 respectiv Delta pozitive așa

cum spuneam când Delta este negativ

parabola nu intersectează axa o

x când Delta este egal cu 0 parabola

intersectează axa o x în un singur

punct cântărește pozitiv intersectează

axa o x în două puncte distincte

parabolă este convexă deține în

aceste condiții reprezentările

grafice corespunzătoare acestor

categorii acestor situații teoretice

sunt următoare Deci parabola nu

atinge axa o x parabola dar vedeți

Avem mai multe reprezentări de

funcții de gradul al doilea the

street parabolele fără a da valori

și așa cum spuneam Delta negativ

nu atingi axa o x Delta egal cu

0 atinge axa o x sunt un singur

punct alte parabolă care atinge

un singur punct încă o dată spune

ține apă Da deci convex și atunci

când Delta este pozitiv intersectează

în două puncte axa o x și acum

am lămurit noi intersectează punctele

astea în care intersectează în

singur punct Da respectiv celelalte

două câte două da puncte de intersecție

distincte cu spunea cu Axa o x

așa cum spuneam în realitate acesta

reprezintă X1 egal cu x 2 de terminat

din ecuația de gradul al doilea

acesta reprezintă iar X1 egal cu

x Deci confundat reală pe axa reală

o x egal măsură situația în care

X1 este acesta este acesta și cum

vedem distincte Da nu sunt aflat

în același punct sunt confundat

la fel aceeași poveste și aici

foarte important e să înțelegeți

că în realitate momentul în care

am afirmat ecuația de gradul al

doilea corespunzătoare mai Clara

x pătrat plus bx plus c egal cu

zero Am afirmat de fapt sau am

făcut de fapt intersecția graficului

CD cu Axa o x va duceti aminte

că atunci când ne propunem să faci

în intersecția graficului cu Axa

o x însemna să fac De fapt de x

egal cu 0 sau y10 când dorea să

fac Intersecția cu oe spuneam x

egal cu zero acum mă interesează

strict Intersecția cu Axa o x 10

repet momentul în care am afirmat

ecuație de gradul al doilea corespunzătoare

în realitate aceasta a însemnat

intersecție a graficului funcției

De ce apar aburi cu Axa o x așa

cum practică ați văzut și în reprezentările

grafice comentate a doua situație

pe aceea în care așa cum spuneam

aude era negativ se face pe exact

același principiu de discuții astfel

că Intersecția cu Axa o x reprezenta

f de x egal cu 0 Deci y egal cu

0 ecuația de gradul al doilea care

conțin se poate afla în trei situații

discutate distincte și anume Delta

negativ Delta egal cu 0 Delta pozitiv

situația cu Delta negativ nu mai

avea soluții reale în situația

cu Delta egal cu 0 are soluțiile

a lexicale mai clar confundate

situația în care Delta era pozitiv

are soluții distincte rea nu stați

în care așa cum nu am exprimat

clar vorbim de situația în care

nu intersectează axa o x în d pe

negativ când Delta egal cu 0 intersectat

un singur punct când Delta este

pozitiv intersectează în două puncte

distincte mai mult decât atât Atunci

când a este negativ înțelegem că

parabola Este cam Deci situația

cea care nu vine apă exact același

principiu putem comenta cele trei

situații distincte ale problemei

și anume funcția f definită pe

r cu valori în aer cu f de x egal

cu x pătrat plus bx plus c și a

negativ este situația așa cum spuneam

mâncare parabola nu țin Da și pe

fiecare din situațiile discutate

Când este negativ nu intersectează

axa o x da intersectează întru

un singur punct spectiv intersectează

în două puncte distincte axei o

x așa cum spuneam se vede clar

că nu intersectează acestea sunt

practic rădăcini X1 X2 egal cu

fondate aici X1 X2 X1 X2 În egală

măsură 60 sunt doi diferite