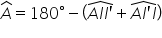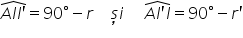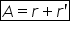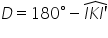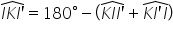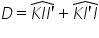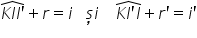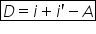Prisma. Formarea imaginilor. Oglinzi plane şi sferice.

în cea de a doua lecție de optică

geometrică vom discuta despre prisma

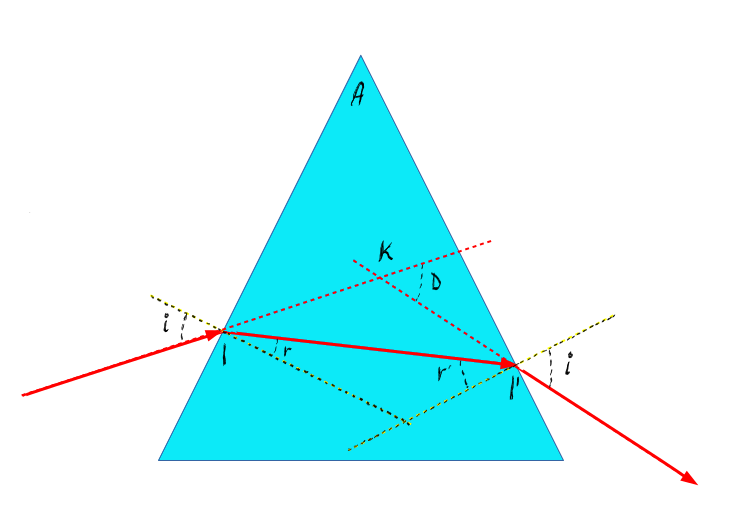
și oglinzi prismă optică e făcută

din sticlă și are forma triunghiulara

are două unghiuri principale unghiul

a de la Vârful prismei și deviația

totală a prismei notată cu de între

raza incidență și raza emergente

cu linii galbene întrerupte desenăm

normale la cele două suprafețe

ale prismei în punctele de incidență

pentru a calcula unghiul a Considerăm

unghiurile din triunghiul a e e

prim și observăm că a este egal

cu 180 de grade minus suma dintre

unghiul A e e prim și a e e unghiul

A e e prim este egal cu 90 de grade

minus unghiul R aceasta deoarece

după cum ați sus linia întreruptă

galbenă este normală Deci perpendiculară

pe suprafață și cele două unghiuri

suma lor va fi egală cu 90 de grade

identic a va fi egal cu 90 de grade

minus R prin din aceste trei ecuații

ne ducem relația pentru unghiul

prismei a Care este egal cu a plus

aer prin aceasta este prima ecuația

prismei pentru unghiul de observăm

că suma dintre unghiul d și unghiul

e k e prim este egal cu 180 de

grade deci de este 180 de grade

minus e ca E prim unghiul e c a

prim la rândul lui este 180 de

grade minus suma dintre unghiurile

k e e prim și ca ai primi aceasta

deoarece cele trei unghiuri formează

triunghiul ca e prima Deci combinând

la aceste două relații de este

egal cu Hai prim plus ca ai primi

pentru a calcula aceste două unghiuri

Considerăm unghiurile din jurul

punctului e și prin și observăm

că ca e e prin plus Air preț suma

acestor două unghiuri este egală

cu unghiul e pentru că sunt delimitate

de aceleași taxi deci putem scrie

ca e e prim plus R este egal cu

e și la fel ca ai primi plus R

prim egal cu a prim Deci poate

fi scris ca imi nose plus eeprom

minus R prim și în sfârșit luând

în considerație formula pentru

unghiul prismei a a avem că d este

plus e prim minus a aceasta fiind

cea de a doua relație a prismei

vom vorbi acum despre formarea

imaginilor în prima lecție de optică

geometrică că am văzut că un obiect

emite raze de lumină în toate direcțiile

Deci aceste raze vor forma un fascicul

Divergent din obiect Dacă aceste

raze de lumină întâlnesc suprafața

de separare cu un alt mediu omogen

vom avea fenomenele de reflexie

și refracție întrebarea care se

pune este putem folosi intru mod

inteligent aceste fenomene de reflexie

și refracție a astfel încât să

obținem O re convergență parțială

acestor raze între anumit punct

dacă reușim acest lucru acest punct

se va numi imaginea obiectului

original instrumente optice precum

oglinda care folosește reflexia

sau lentila care folosește refracția

generează această de convergență

a razelor pornind din un obiect

un alt punct numit imagini Deci

imaginea este intersecția razelor

ce pleacă din tu un obiect prin

fenomenul de reflexie sau reflecție

ia poate fi reală dacă are loc

la intersecția razelor după ca

ma vede am văzut sau virtuală la

intersecția prelungirilor razelor

după cum vom vedea imediat primul

instrument Optic și cel mai simplu

instrument Optic totodată care

produce imagini virtuale prin reflexie

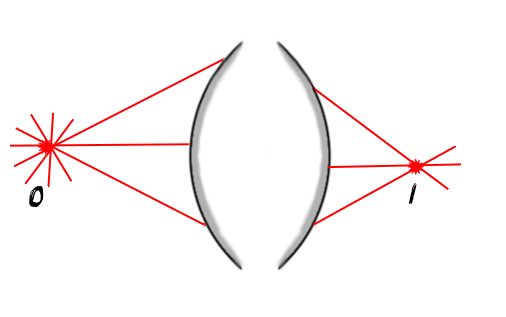
este oglinda plan Linda plană este

o suprafață plană ce reflectă razele

de lumină Să considerăm un obiect

care emite raze în toate direcțiile

și în particular spre dreapta unde

se află o oglindă plană acest segment

îngroșat alb bineînțeles oglinda

plana va reflecta aceste Raise

fasciculul reflectat este și el

Divergent pentru că cu cât punctul

de incidență este mai departe de

obiect unghiul de incidență este

mai mare și Deci și unghiurile

de reflexie sunt mai mari Deci

fasciculul reflectat este divergente

razele reflectate nu se vor întâlni

totuși prelungirile lor se vor

întâlni pentru un punct numit imagini

Deci cu roșul avem imaginea acestui

obiect în concluzie oglinda plana

formează imagini virtuale pentru

că se formează la intersecția prelungirilor

razelor reflectate răsturnată este

de cealaltă parte a cuprins II

și egal pentru că distanța dintre

imagine și oglindă este egală cu

cea dintre oglindă și obiect un

exemplu de oglindă plană pentru

aplicații practică este oglinda

retrovizoare a unui automobil vom

vorbi acum despre un alt Optic

și anume oglinda sferica Ea este

de două tipuri concavă și convexă

oglinda concavă are reflecția pe

suprafața interioară deci numai

razele ce vin dinspre centrul oglinzi

vor fi reflectate dreapta si trece

prin centrul oglinzi și vârful

oglinzii se numește axa optică

principală de desenat aici cu alb

și întreruptă și are proprietate

importantă că orice rază incidentă

de a lungul axei optice principale

va fi reflectată tot pe axa optică

principală orice altă dreaptă ce

trece prin centrul oglinzii se

numește axa optică secundară și

are aceeași proprietate importantă

și anume că o rază incidența de

a lungul a reflectată tot pe ea

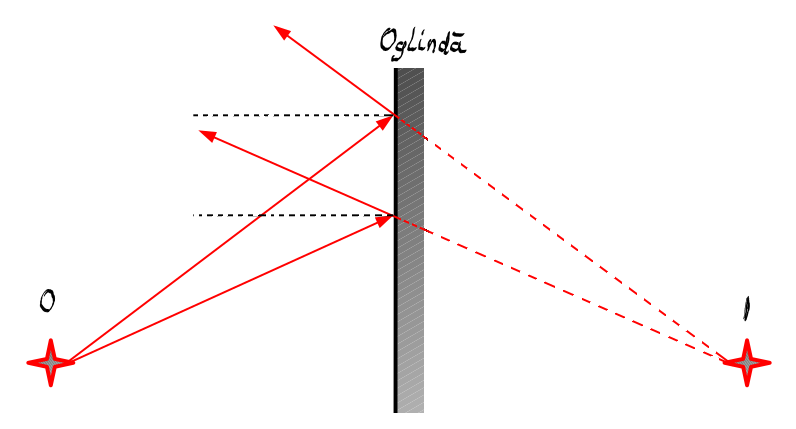
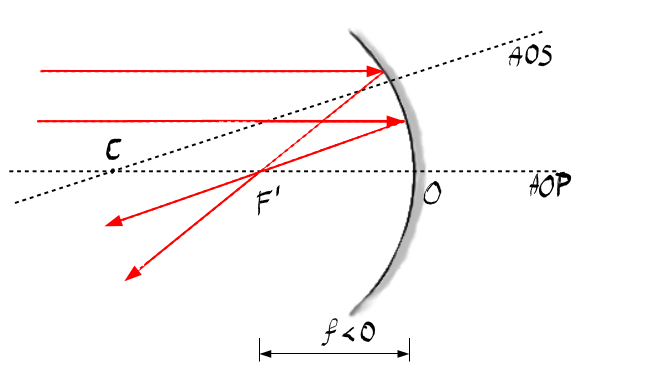
razele paralele cu Axa optică principală

sunt reflectate prin focarul principal

imagine notat cu exprimă aici aceste

două raze sunt incidente paralel

cu Axa optică principală și apoi

sînt reflectate prin focarul principal

imagine distanța dintre vârful

oglinzi concave o și focarul principal

imagine se notează cu e f f prim

și este considerată prin convenție

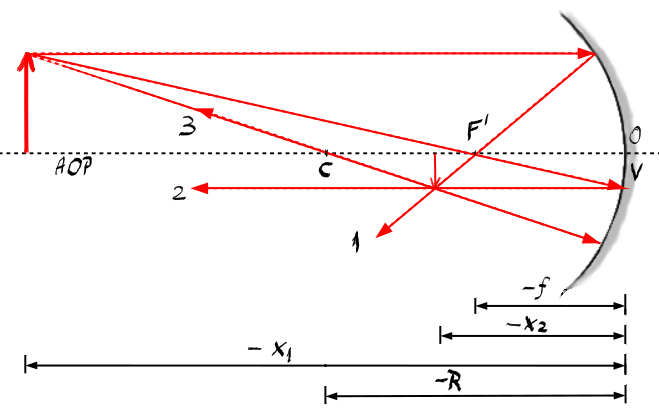
negativ oglinda convexă are reflexia

pe partea exterioară deci numai

razele ce vin din partea opusă

si centrului oglinzii vor fi reflectate

au aceleași axa optică principală

și secundară ca secundare ca și

oglinda concavă iar razele paralele

cu Axa optică principală ca acestea

doua sunt reflectate astfel încât

prelungirile lor se întâlnesc în

focarul principal obiect distanța

dintre vârful oglinzii convex și

focarul principal obiect f se notează

cu m și este considerată prin convenții

pozitiv cel mai important lucru

de ținut minte la oglinzile sferice

sunt aceste cazuri particulare

de razei incidente și anume razele

Da lungul axei optice vor fi reflectate

tot pe axa optică iar apoi razele

incidente paralel cu Axa optică

vor fi reflectate prin focar în

ambele cazuri iar cele ce sunt

incidente plin focar vor fi reflectate

paralel cu Axa optică principală

sau secundară dacă e casă folosind

aceste raze particulare să construim

imagini în Oglinzi sferice ce vedeți

aici în trei culori albastru roșu

și verde sunt cele trei tipuri

de raze despre care tocmai am vorbit

să le folosim pentru a construi

imaginea obiectului ab în oglinda

concavă din această schemă de ce

acest caz ne arată o oglindă concavă

cu un obiect care se află dincolo

de centrul oglinzii de este mai

mare decât el și mai mare decât

ea respectiv și în concluzie folosim

cele trei roz cu albastru raza

paralel cu Axa optică principală

și apoi reflectată prin focar cu

roșu raza incidentă prin focar

și apoi reflectată paralel cu Axa

optică principală și cu verde raza

incidentă prin centrul oglinzii

care apoi este reflectată Tot prin

acest centru asta deoarece dreapta

BC este o axă optică secundară

la intersecția celor trei raze

obținem imaginea obiectului notat

aici cu a prim b prim în concluzie

în acest caz 1 obținem o imagine

cu următoarele proprietăți este

reală pentru că se formează la

intersecția razelor și nu la intersecția

prelungirilor lor este răsturnată

față de obiect după cum se vede

și este mai mic următorul cald

este cel în care obiectul se află

de data aceasta între centrul oglinzii

și focar Deci cazul oglindă concavă

și obiectul situat astfel încât

R raza oglinzi este mai mare decât

de poziția obiectului mai mare

decât ea cele trei raze cu albastru

incidenta paralel cu Axa optică

reflectata prin focar cu roșu incidenta

infocar reflectată raza reflectată

paralelă cu Axa optică și în sfârșit

incident apara prin centrul Optic

reflectată Tot prin centrul Optic

al oglinzii la intersecția lor

sub forma imaginea notată cu a

prim D prim și aceasta are următoarele

proprietăți este reală din nou

se formează la intersecția rațelor

nu ei prelungirilor este răsturnată

față de obiect și este mai mare

un al treilea caz pe care îl facem

în această lecție este cel în care

obiectul AB se află între vârful

oglinzii și focar Deci avem o oglindă

concavă din nou și obiectul poziționat

astfel încât raza oglinzi e mai

mare decât distanța focală mai

mare decât de tras în cele trei

raze În primul rând cu albastru

raza incidentă paralelă cu Axa

optică va fi reflectată plin focar

cu roșu raza incidentă prin focar

reflectată paralel cu Axa optică

și raza incidentă prin centrul

oglinzii va fi reflectată prin

centru după cum se vede ele se

intersectează doar în prelungirile

lor pentru că după cum se vede

razele reflectate formează un fascicul

Divergent Deci imaginea formată

are următoarele proprietăți este

virtuală de data asta pentru că

se formează la intersecția prelungirilor

razelor este dreaptă față de obiect

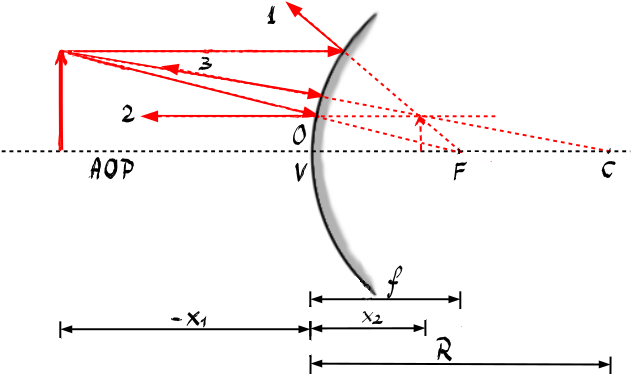
și este mai mare un ultim caz de

imagine pe care o facem este cel

al unei oglinzi convexe de data

aceasta pentru că obiectul se află

de partea opusă centrului oglinzii

și deci în acest caz poziția după

cum vedea vom vedea obiectului

nu mai știi importantă Deci avem

o oglindă convexă situată la o

distanță de soare care față de

vârful oglinzi cele trei raze cu

albastru Roz la paralelă cu Axa

optică care apoi este reflectată

astfel încât prelungirea a trece

prin focar cu roșu raza incidentă

prin focar între lungimea ei Care

a fost reflectată paralel cu Axa

optică și cu verde raza incidență

prin centru în Prelungirea ei care

apoi este reflectată Tot prin Centru

Evident aceste trei raze reflectate

sunt formează un fascicul Divergent

DEX se intersectează doar în prelungirile

lor Deci Imaginea a prim b prim

are următoarele proprietăți este

virtuală adică se formează la intersecția

prelungirilor este dreaptă în raport

cu obiectul și este mai mică notăm

că acest tip de oglindă și anume

convexă poate fi întâlnită des

ori în trafic pentru magnificare

detaliilor străzilor sau diferitelor

semne de