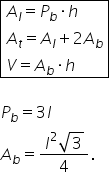Prisma triunghiulară regulată (aplicații)

în această secvență pomul de duce

împreună formulele cele mai des

întâlnite în probleme legate de

prismă triunghiulară regulată și

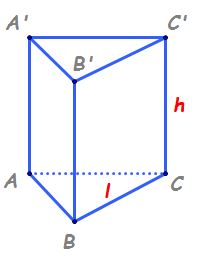
să ne amintim pentru început Care

sunt elementele unei prisme triunghiulare

regulate în primul rând iar a două

baze situate în plane paralele

iar bazele sunt reprezentate de

două triunghiuri atenție echilaterale

și congruente fețele laterale sunt

reprezentate de trei dreptunghiuri

și ele congruente cu alte cuvinte

muchiile laterale sunt congruente

și oricare din aceste trei muchii

laterale poate fi considerată înălțime

a prismei și să începem cu aria

laterală să vedem ce este aria

laterală aria laterală este suma

ariilor fețelor laterale bun care

sunt fetele laterale Păi avem trei

dreptunghiuri congruente Și atunci

vom face următoarele notații vom

nota cu h înălțimea acestei prime

știind că toate sunt congruente

și o să notăm cu l mic lungimea

muchiei bazei și acum aria laterală

se notează cu a indice al și este

suma ariilor fețelor laterale Păi

cum avem trei fețe congruente vom

trece aici egal cu 3 înmulțit cu

aria unei fețe am spus că o față

este un dreptunghi care are dimensiunile

L mic și h Deci avem l mic ori

H însă Ce reprezintă trei ori el

Păi de prezintă de fapt perimetrul

bazei pentru că baza este un triunghi

echilateral deci putem să scriem

formula aria este egală cu perimetrul

bazei înmulțit cu înălțimea 1 Ce

înseamnă acum sau Ce înțelegem

acum prin arie totală e simplu

de bănuit aria totală este suma

ariilor tuturor fețelor prismei

cu alte cuvinte aria totală este

alcătuită din aria laterală adunată

cu ariile celor două baze cu bazele

sunt congruente înseamnă că putem

să scriem 2 înmulțit cu aria bazei

și acum Cu cât este egală aria

bazei de bază este un triunghi

echilateral cu lungimea laturii

de el să spunem el centimetri atunci

aria unui triunghi echilateral

este egală cu latura la a doua

radical din 3 supra 4 poate cuvinte

determina aria totală trebuie să

înlocuim aria laterală cu cea este

scrisă aici Iată și apoi adunăm

de două ori aria bazei și aria

bazei este notat aici să vedem

acum care este și volumul unei

prisme triunghiulare regulate volumul

formula volumului este dată de

aria bazei înmulțită cu înălțimea

sigur dacă vrem putem să și detaliem

de Ce rezultă că volumul este egal

cu aria bazei știind Cât este avem

aici el la el la 2 radical din

3 supra 4 înmulțit cu h și vom

obține aici și centimetri cubi

dacă am spus că vorbim în centimetri

acestea sunt formulele pe care

le vom folosi de de sunt probleme

Deci reținem că pentru o prismă

triunghiulară regulată aria laterală

este egală cu produsul dintre perimetrul

bazei și înălțimea prismei aria

totală are această formulă Iată

trebuie să adunăm aria laterală

cu dublul ariei bazei bun încadrăm

și pe aceasta aria bazei știm deja

formula de formula ariei unui triunghi

echilateral și formula pentru determinarea

volumului unei prisme triunghiulare

regulate aria bazei înmulțită cu

înălțimea