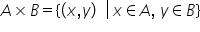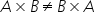Produsul cartezian a două mulțimi
Tag-uri
Partajeaza in Google Classroom
Transcript
produsul cartezian a doua mulțimi
sistem de axe ortogonale Fie a
și b două mulțimi nevide produsul
cartezian al mulțimilor a și b
se notează cu a ori b și este format
din toate perechile ordonate de
forma x y unde x este un element
al mulțimii A și y este un element
al mulțimii B să facem un exemplu
Fie mulțimea A formată din elementele
doi și trei și mulțimea b formată
din numerele 4 5 și 6 să calculăm
produsul cartezian a ori b mai
întâi vom lua primul element al
mulțimii A și al grupând cu fiecare
element al mulțimii b apoi continuăm
cu al doilea element al mulțimii
A și lucru pom pe rând cu fiecare
element din mulțimea b prima pereche
va fi 2 4 urmează doi cinci doi
șase și acum continuăm cu al doilea
număr din mulțimea A și formăm
perechile 3 4 35 și 36 acesta este
produsul cartezian a ori b rețineți
că produsul cartezian nu este comutativ
pentru că A ori B va fi diferit
de b ori a Haideți să calculăm
și produsul b ori a pentru acest
produs vom începe cu elementele
mulțimii d și le grupăm pe rând
cu elementele mulțimii a primul
număr din mulțimea b este 4 și
atunci formă în perechi care încep
cu 442 patru trei continuăm cu
al doilea număr din mulțimea A
B și formăm perechile cinci doi
cinci trei și ultimele două perechi
sunt șase doi e63 observăm Așadar
că A ori B este diferit de b ori
a un alt exemplu Fie mulțimea A
formată din numerele 0 și 1 și
mulțimea b formată din numărul
8 Moon calcula produsul cartezian
a ori b începem cu elementele mulțimii
a și pe urmă perechea 0 8 și unu
opt acestea doua sunt cele două
elemente ale produsului cartezian
a c elementele unui produs sunt
perechi un alt exemplu avem mulțimea
A formată din numărul 10 și mulțimea
b formată din elementele 3 5 și
9 produsul cartezian a ori b va
fi format din următoarele perechi
de numere 10 3 10 5 și 10 9 în
continuare o să vedem cum putem
să Reprezentăm grafic elementele
unui produs cartezian pentru a
reprezenta geometric produsul cartezian
a doua mulțimi avem nevoie de un
sistem de axe ortogonale construim
două axe perpendiculare iar punctul
de intersecție al celor două drepte
se va numi originea sistemului
ortogonal și se notează cu litera
o pe cele două axe alege aceeași
unitate de măsură asta o x se va
numi axa absciselor iar axa o x
se numește axa ordonatelor ne propunem
să Reprezentăm grafic produsul
cartezian al mulțimilor a egal
1 și 2 și b mulțimea formată din
numerele 3 și 4 mai întâi să scriem
elementele mulțimii a ori b aceasta
va conține următoarele perechi
de numere perechea 1 3 perechea
1 4 perechea 2 3 și doi patru pentru
a reprezenta grafic aceste puncte
mai întâi vom reprezenta pe una
din axa elementele mulțimii A iar
pe cealaltă axă elementele mulțimii
B reprezentat pe axa o x numerele
1 și 2 iar pe axa o y că avem numerele
3 și 4 iti este trei și aici avem
numărul 4 și acum trebuie să Reprezentăm
prima pereche formată din numerele
1 și 3 1 c o paralelă la axa o
y punctat iar de la 3:00 ducem
o paralelă la axa o x punct us
punctul în care se intersectează
cele două drepte va fi reprezentarea
grafică a pereche 1 3 voi nota
acest punct cu litera m mă îmi
spune că punctul m are coordonatele
1 și 3 a doua pereche 1 4 de la
1:00 ducem paralele la axa o y
iar de la 4 conduce o paralelă
la axa o x iar punctul în care
se intersectează cele două paralele
va fi punctul n și mă spune că
n are coordonatele 1 și 4 următoarea
pereche 2 3 de la 2:00 ducem o
paralelă la axa o y pe la 3:00
avem deja desenată paralela la
axa o x și atunci punctul în care
se intersectează aceste două paralele
va fi un al treilea punct notat
cu p pe de coordonate 2 3 și ultima
pereche 2 4 avem deja desenate
paralelele de la 2:00 și de la
4:00 cu axele o x și o y și atunci
punctul de intersecție al acestora
drepte va fi punctul q de coordonate
2 4 cele patru puncte constituie
reprezentarea geometrică a produsului
cartezian a ori b
Produsul cartezian a două mulțimiAscunde teorie X
Navigare în lectii
Cumpara abonament
