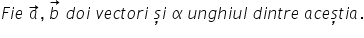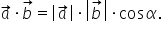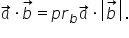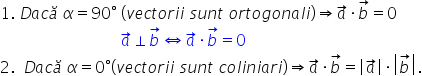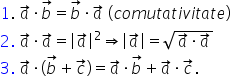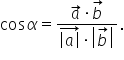Produsul scalar a doi vectori
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție vom defini o
operație care Asociază unei perechi
de vectori un număr real iar această
operație se numește produs scalar
această noțiune este des întâlnită
în fizică de exemplu lucrul mecanic
este produsul scalar dintre vectorul
forță și vectorul deplasare pentru
a defini produsul scalar a doi
vectori mama Cezar cei doi vectori
astfel încât să aibă aceeași origine
și voi nota cu alfa unghiul dintre
aceștia produsul scalar al vectorilor
a și b se notează astfel a ori
b și este egal prin definiție cu
modulul vectorului a înmulțit cu
modulul vectorului b ori cosinus
de Alfa această relație se mai
poate scrie și astfel a ori b egal
cu modul de a ori coș de Alfa ori
modulul vectorului b dacă duc prin
extremitatea vectorului a o perpendiculară
pe dreapta suport a atunci se obține
aici proiecția vectorului a pe
dreapta b ne uităm în acest triunghi
dreptunghic și avem cos de Alfa
egal cu raportul dintre catetele
tu rată și ipotenuză cateta alăturată
este proiecția vectorului a pe
dreapta b iar ipotenuza este modulul
vectorului a prin urmare modul
de a ori cos de Alfa este egal
cu proiecția vectorului a pe dreapta
b și acum revenind la această relație
și înlocuind modul de aur cos de
Alfa cu proiecția vectorului a
pe dreapta b produsul scalar se
mai poate scrie astfel a ori b
egal cu proiecția vectorului a
pe dreapta b ori modulul vectorului
b Aceasta este o altă modalitate
de a scrie produsul scalar a doi
vectori în cazul în care unghiul
Alfa are măsura egală cu 90 de
grade atunci cei doi vectori se
numesc ortogonali în acest caz
produsul scalar al vectorilor a
și b este egal cu modulul vectorului
a ori modulul vectorului b ori
cosinus de 90 de grade Care este
zero prin urmare doi vectori a
și b sunt ortogonali dacă și numai
dacă produsul scalar este egal
cu 0 dacă vectorii sunt coliniari
și au același sens atunci unghiul
Alfa are măsura egală cu 0 situație
produsul scalar este egal cu modulul
vectorului a ori modulul vectorului
b ori post de 0 grade Care este
egal cu 1 prin urmare produsul
scalar a doi vectori coliniari
având același sens este egal cu
produsul modulelor lor să vedem
în continuare câteva proprietăți
ale produsului scalar o prima proprietate
produsul scalar este comutativ
deci a ori b este egal cu b ori
am comutativitatea înmulțirii numerelor
reale conduce și la comutativitatea
produsului scalar întrucât modulul
vectorului a și modulul vectorului
b sunt numere a doua proprietate
produsul scalar al unui Vector
cu el însuși a ori a va fie egal
cu modulul vectorului a înmulțit
cu modulul vectorului a ori coș
de 0 grade Care este egal cu 1
de ce dar mai departe cu modulul
vectorului a la pătrat de aici
putem deduce că modulul unui Vector
este rădăcina pătrată a produsului
scalar al vectorului cu el însuși
și eu altă proprietate produsul
scalar este distributiv față de
adunarea vectorilor de a ori b
plus c este egal cu produsul scalar
al vectorilor a și b plus a ori
c din această relație putem să
exprimăm cosinus de Alfa și vom
obține produsul scalar al vectorilor
a și b supra modul de a ori modul
de B aceasta este formula prin
care putem să calculăm cosinusul
unghiului dintre cei doi vectori
și în continuare vom face 2 Exerciții
primul exercițiu se dă pătratul
ABCD cu latura având lungimea egală
cu șase unități se cere sa calculăm
produsul scalar al vectorilor ab
și ac acesta va fi egal cu modulul
vectorului ab ori modulul vectorului
AC ori cosinusul unghiului dintre
cei doi vectori din moment ce abcd
este pătrat iar AC este diagonală
unghiul Acesta are măsura egală
cu 45 de grade de ce avem aici
colț de 45 egal a b este 6 lungimea
vectorului a c se poate calcula
foarte ușor cu teorema lui Pitagora
AC la pătrat este egal cu 6 la
pătrat plus 6 la pătrat obținem
că AC este egal cu 6 radical din
2 deci modulul vectorului a c este
6 radical din 2 iar posibil de
45 de grade este radical din 2
pe 2 egal cu 36 și al doilea exercițiu
Se dă triunghiul abc în care ab
are lungimea egală cu patru unități
AC are șase unități măsura unghiului
BAC este egală cu 60 de grade m
este mijlocul lui bc b c a m este
mediană și se cere să calculăm
modulul vectorului a m vă reamintesc
că modulul unui Vector la pătrat
este produsul scalar al vectorului
cu el însuși vom calcula mai întâi
modul de m la pătrat pentru aceasta
voi prelungii segmentul a m cu
un segment având aceeași lungime
cu acesta sa format astfel un patrulater
în care m este mijlocul diagonalelor
prin urmare Patrulaterul abdc este
un paralelogram și acum vom considera
vectorii AB AC și a m observăm
că a m este jumătate din ad dar
AD este suma vectorilor ab și ac
vrei amintesc că suma a doi vectori
este diagonala paralelogramului
având ca laturi cei doi vectori
prin urmare modulul vectorului
a m la pătrat este egal cu a m
ori a m Adică 1 supra 4 pe lângă
ab plus AC ori ab plus și acum
desfacem parantezele și avem unul
pe 4 pe lângă a b ori a b plus
a b ori a c plus ace ori ab plus
pace ori ac egal cu 1 pe 4 pe lângă
a b ori a b este modul de a b la
pătrat plus ab ac plus AC ori ab
este egal cu 2ab ori AC iar AC
ori AC este modul de acela pătrat
egal cu 1 pe 4 pe lângă modul de
a b la pătrat este 4 la a doua
16 modulului acela pătrat este
6 la a doua 36 plus 2 ori aici
avem produsul scalar al vectorilor
ab și ac adică patru ori 6 ori
cosinusul unghiului dintre aceștia
Deci cosinus de 60 de grade egal
cu 1 pe 4 pe lângă 52 plus 24 8
ore 648 ori cozi de 60 1 pe 2 egal
cu 1 pe 4 ori 52 plus 24 este 7676
se simplifică cu patru uși ne rămâne
în 19 Deci modul de a m la pătrat
este egal cu 19 prin urmare modulul
vectorului a m a fi egal cu radical
din 19