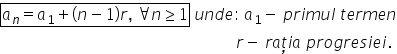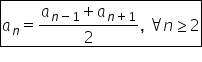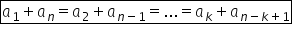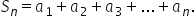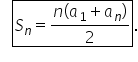Progresii aritmetice (aplicații)

în această secvență o să facem

câteva exerciții în care o să aplicăm

proprietățile progresiei aritmetice

am scris în partea dreaptă cele

mai importante formule pe care

o să le folosim în exerciții Și

începem cu primul exercițiu se

dă progresia aritmetică a 1 a 2-a

n Se știe că al treilea termen

este 4 al 15-lea termen este 10

și se cere să calculăm l37 la termen

și suma primilor 37 de termeni

folosim aceste două relații și

vom scrie cei doi termeni a trăi

și a 15 în funcție de primul termen

și de rație folosind această primă

formulăm Așadar ar3 va fi egal

cu a 1 plus 3 minus 1 adică 2 r

iar acest termen este egal cu 4

și a 15 este egal cu a 1 plus 15

minus 1 adică 14 egal mai departe

cu 10 din aceste două relații putem

să formăm un sistem de Două ecuații

cu două necunoscute prima ecuație

va fie a 1 plus 2 R egal cu 4 și

2-a ecuație A1 plus 14 R egal cu

10 rezolvăm acest sistem prin metoda

reducerii înmulțim prin mai încoace

cu minus 1 și adunăm Cele Două

ecuații se reduce a 1 minus 2 r

plus 14 R este egal cu 12 R minus

4 plus 10 este egal cu 6 obținem

Așadar R egal cu 6 supra 12 de

unde rezultă că el este egal cu

1 supra 2 am obținut trei zile

progresiei aceasta este egală cu

1 pe 2 Acum putem să calculăm primul

termen Revenim la prima ecuație

a 1 plus 2 ori Înlocuim pe r cu

1 supra 2 egal cu 4 se simplifică

2 echivalent a 1 plus 1 este egal

cu 4 echivalente a 1 este egal

cu 3 am obținut și primul termen

al progresiei acesta este egal

cu 3 Acum putem să calculăm a37

aprindem din nou prima formulă

și egal cu a 1 plus 36 egal mai

departe cu 3 plus 36 ori 1 pe 2

egal cu 3 plus se se gliffy că

36 cu doi Rămâne 18 și el mai departe

cu 21 și a b să calculăm suma primilor

37 de termeni calcul alăturat aplicăm

ultima formulăm s37 va fi egal

cu 37 pe lângă A1 este 3 plus a

37 este 21 totul supra doi egal

cu 37 ori 24 totul supra 2 se simplifică

24 cu 2 obținem 37 ori 12 și egal

cu 444 continuăm cu al doilea exercițiu

Să se afle numărul real x astfel

încât numerele 2 x plus 5 3x plus

11 și 13 x minus 1 să fie în progresie

aritmetică nu știm că în orice

progresie aritmetică fiecare termen

începând cu al doilea este media

aritmetică a vecinilor săi Așadar

în acest exercițiu vom aplica această

formulă a n egal cu a n minus 1

plus a n plus 1 totul supra 2 din

urmare termenul din mijloc adică

3x plus 11 a fi media aritmetică

a celorlalți doi termeni 2x plus

cinci plus 13 x minus 1 totul supra

2 2 pe lângă 3x plus 11 este egal

cu 2x plus 13 x adică 15 x plus

4 6x plus 22 egal cu 15 x plus

4 9 x este egal cu 18 x este egal

cu 2 și al treilea exercițiu fie

a 1 a 2-a n o progresie crescătoare

în care sunt îndeplinite relațiile

a 1 a 2-a 3 egal cu 162 și A1 plus

A2 plus A3 egal cu 18 se cere să

calculăm suma primilor 20 de termeni

mai întâi vom folosi a doua relație

dată în problema pe care o să mai

scriu o dată A1 plus A2 plus A3

este egal cu 18 m scrie termenii

a 1 și a 3 în funcție de A2 A3

este A2 plus rația iar A1 este

a 2-a minus rația și adunând acești

termeni obținem 18 observăm că

dacă am scris Cei trei termeni

în modul acesta se reduce R și

obținem astfel o ecuație cu o singura

necunoscută 3-a 2 este egal cu

18 de unde rezultă că a2 este egal

cu 6 pentru a afla suma primilor

20 de termeni mai trebuie să aflăm

A1 și rația folosim această relație

a 1 a 2-a 3 egal cu 162 1 am zis

că este a 2 minus 3 ori a 2 ori

a treia este 2 plus rația și egal

cu 162 acum Înlocuim pe A2 cu șase

și inversez locul primilor doi

factori 6 pe lângă 6 minus R pe

lângă 6 plus R egal cu 162 6 pe

lângă om 6 la a doua minus y la

a doua egal cu 162 36 minus aer

la pătrat este egal cu 162 împărțit

la șase adică 27 er la pătrat este

egal cu 36 minus 27 adică 9 acum

o să fac o mică paranteză dacă

avem o progresie aritmetică cu

rația pozitivă atunci acea progresie

aritmetică a n este un șir strict

crescător iar dacă rația este negativă

atunci progresia a n este un șir

strict descrescător nu știm din

datele problemei că progresia este

crescătoare Așadar deși avem aici

o ecuație de gradul 2 cu două soluții

3 și minus 3 din moment ce probe

licia este crescătoare singura

soluție posibilă este cea pozitivă

Așadar rația va fi egală cu 3 Acum

putem să calculăm primul termen

voi continua alăturat A1 este a

2-a minus ra2 este 6 3 6 minus

3 3 pentru a calcula s20 mai trebuie

să calculăm termenul de rang 20

acesta este egal cu a 1 plus 19

el și el mai departe cu 3 plus

19 ori 3 egal 3 plus 50 și 760

s20 va fi egal cu 20 pe lângă A1

este 3-a 20 este 60 totul supra

2 egal se simplifică 63 ori 10

egal cu 630