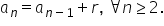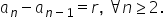Progresii aritmetice - noțiuni introductive
Tag-uri
Partajeaza in Google Classroom

Transcript
Mai țineți minte acele probleme
de logică în care aveam o secvență
și trebuia să ghicim Ce număr urmează
Haide să vedem dacă reușim să scriem
numărul care urmează în fiecare
dintre cele trei secvențe în prima
secvență a vem numerele 1 3 5 7
9 11 13 15 este foarte ușor de
observat faptul că fiecare număr
se obține din numărul precedent
la care se adaugă numărul 2 Așadar
numărul care urmează va fi 15 plus
doi adică 17 în a doua secvență
avem numerele minus 20 minus 15
minus 10 minus 5 0 5 și 10 observăm
că în acest caz fiecare număr se
obține din numărul precedent la
care se adaugă 5 așa dar aici o
să avem 10 plus cinci adică 15
și în a treia secvență avem numerele
1 minus 2 minus 5 minus 8 minus
11 minus 14 minus 17 în acest caz
putem observa că fiecare număr
se obține din numărul precedent
din care scădem 3 sau mai putem
spune că adunăm numărul minus 3
minus 17 minus 3 va fi minus 20
În astfel de șir în care fiecare
termen se obține din termenul precedent
prin adăugarea a aceluiași număr
se numește progresia aritmetică
în prima secvență am văzut că fiecare
număr se obține din numărul precedent
la care se adaugă numărul 2 acest
număr doi se numește rația progresiei
și se notează cu r Așadar în acest
caz rația este egală cu 2 în a
doua secvență rația este egală
cu cinci și în a treia secvență
rația este egală cu minus 3 Dacă
un șir a n este progresie aritmetică
a tunci notăm acest lucru a astfel
și putem observa că are loc următoarea
relație de recurență a n este egal
cu a n minus 1 plus R oricare ar
fi un număr mai mare sau egal cu
2 Așadar fiecare termen începând
cu al doilea se obține din termenul
precedent la care se adaugă rația
iar primul termen A1 este un număr
real fixat Așadar spunem că o progresie
aritmetică este bine determinată
dacă se cunosc primul termen A1
și rația cu alte cuvinte dacă știm
primul termen și rația Putem să
scriem toți termenii progresiei
aritmetice această relație de recurență
se mai poate scrie și astfel a
n minus a n minus 1 egal cu aer
Așadar Diferența a doi termeni
consecutivi este întotdeauna un
număr constant și acest număr este
chiar rația progresiei Așadar pentru
a verifica dacă un șir este progresia
aritmetică verificăm dacă diferența
a doi termeni consecutivi este
un număr constant Haideți în continuare
să facem două exerciții primul
exercițiu Scrieți primii patru
termeni ai progresiei aritmetice
a n Dacă a 1 este egal cu 5 și
rația este egală cu minus 2 Așadar
primul termen A1 este egal cu 5
al doilea termen a doi se obține
din primul termen A1 la care se
adaugă rația adică 5 plus minus
2 și obținem 3 A3 este egal cu
a 2 plus rația adică 3 plus minus
doi și obținem 1 și al patrulea
termen a 4-a fie egal cu a 3 plus
rația Adică 1 plus minus 2 egal
cu minus 1 și continuăm cu al doilea
exercițiu fie șirul a n în care
termenul general este dat de formula
a n egal cu 3 n minus 5 la punctul
a se cere sa verificăm dacă șirul
este progresie aritmetică iar la
punctul b să scriem primii cinci
termeni ai șirului pentru a verifica
dacă un șir este progresie aritmetică
trebuie să vedem dacă diferența
a doi termeni consecutivi este
constantă adică nu depinde de an
și atunci Haideți să calculăm Diferența
a n minus a n minus 1 egal cu 3
n minus 5 minus pentru a scrie
acum termenul de rang n minus unu
în formula termenului general îl
Înlocuim pe n cu n minus 1 și o
să obținem 3 pe lângă n minus 1
minus 5 egal cu 3 n minus 5 minus
3 n minus 3 minus 5 minus 8 egal
cu 3 n minus 5 minus 3 n plus 8
se reduce 3n cu minus 3 n și obținem
în final 3 observăm Așadar că diferența
a doi termeni consecutivi este
constantă pentru că nu depinde
de an așa dar șirul a n este progresie
aritmetică iar la punctul B trebuie
să scriem primii cinci termeni
ai șirului primul termen este A1
și se obține înlocuind pe nu1 Deci
avem trei ori 1 minus 5 egal minus
2 a 2 este egal cu 3 ori 2 minus
5 6 minus 5 este egal cu 1 A3 este
egal cu 3 ori 3 minus 5 9 minus
5 4-a 4 este egal cu 3 ori 4 minus
5 12 minus 5 7 și a 5 este egal
cu 3 ori 5 minus 5 15 minus 5 10
mai există și o altă modalitate
prin care putem să scriem acești
cinci termeni noi Am calculat la
punctul a diferență a doi termeni
consecutivi iar aceasta este rația
progresiei Așadar rația este egală
cu 3 Am calculat primul termen
A1 acesta este minus doi și atunci
ei doi se poate scrie A1 plus rația
adică minus 2 plus 3 și egal cu
1 a 3 este egal cu a 2 plus rația
Adică 1 plus 3 egal cu 4-a 4 este
A3 plus rația 4 plus 3 egal cu
7 și A5 este A4 plus rația adică
7 plus 3 și egal cu 10