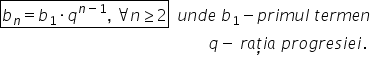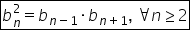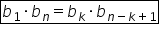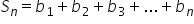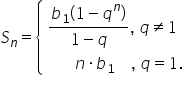Progresii geometrice (aplicații)
Tag-uri
Partajeaza in Google Classroom
Transcript
în această secvență să facem câteva
exerciții cu progresii geometrice
am scris în partea dreaptă principalele
formule pe care o să le folosim
și avem acest prim exercițiul se
dă progresia geometrică B1 B2 bn
Se știe că b 4 este 18 b 6 este
162 se cere să calculăm primul
termen și rația mai întâi pe exprima
de 4 și B6 în funcție de B1 folosind
această formulă de 4 este egal
cu b 1 ori q la a treia și a chest
termeni este egal cu 18 iar b 6
este egal cu b 1 unchiul 5-a și
egal cu 162 acum împărțim aceste
două relații membru cu membru și
obținem B 1-q la 3-a supra b 1-q
la cincea egal cu 18 supra 162
observăm că se simplifică B1 și
el și că am și cu q la a treia
și obținem 1 supra q la pătrat
egal aici se simplifică cu 18 și
ne rămâne unul pe 9 q la pătrat
este egal cu 9 și Avem două soluții
q12 egal cu plus minus trei avem
Așadar două variante posibile mai
întâi dacă rația este egală cu
3 atunci înlocuind pe q în această
relație obținem b 1 ori 3 la a
treia egal cu 18 b 1 ori 27 este
egal cu 18 rezultă B1 egal cu 18
supra 27 se simplifică cu 9 și
obținem 2 pe 3 și a doua posibilitate
dacă rația este egală cu minus
3 atunci înlocuind în aceeași relație
obținem B1 ori minus 3 la a treia
cu 18 de 1 ori minus 27 este egal
cu 18 b 1 este minus 2 supra 3
Așadar această problemă are două
soluții dacă B1 este 2 pe 3 atunci
rația este 3 sau de 1 minus 2 pe
3 și rația este egală cu minus
3 trecem la al doilea exercițiu
Aflați numărul pozitiv x astfel
încât numerele x plus 1 3x și 5
x plus 2 să fie în progresie geometrică
dacă trei numere consecutive sunt
în progresie geometrica atunci
este îndeplinită această relație
și anume pătratul termenului din
mijloc este egal cu produsul vecinilor
săi pentru că numerele x plus 1
3x și 5 x plus 2 să fie în progresie
geometrică va trebui Așadar îndeplinită
relația 3 x la pătrat să fie egal
cu x plus 1 pe lângă 5x plus 2
9 x la pătrat este egal cu 5 x
la pătrat plus 2x plus 5x plus
7 x plus 2 trecem toți termenii
un membru 4 x la patrat minus 7
x minus doi este egal cu zero avem
o ecuație de gradul 2 Delta este
b pătrat minus 4 ac egal cu minus
7 la pătrat minus patru ori patru
ori minus 2 egal cu 49 plus 4 x
4 16 ori 232 și egal cu 81 x 1
este minus b plus radical din deltă
supra 2-a egal minus minus 7 este
7 plus radical din Delta 9 supra
2 ori 4 egal cu 16 supra 8 și egal
cu 2 iar x 2 este minus b minus
radical din deltă supra 2-a egal
u 7 minus 9 supra 2 ori 4 egal
cu minus 2 supra 8 egal cu minus
1 supra 4 însă problema cere ca
x să fie număr pozitiv Așadar soluția
problemei este x egal cu 2 și al
treilea exercițiu se dă suma s
egal cu 3 pe 10 plus 3 supra 10
la pătrat plus și așa mai departe
plus 3 supra 10 la n se cere să
calculăm s minus 1 pe 3 mai întâi
o să calculăm suma s observăm că
avem aici o sumă de n termeni în
progresie geometrică primul termen
al progresiei geometrice b 1 este
3 supra 10 iar rația progresiei
este egală cu 1 pe 10 pentru a
calcula suma s vom aplica Așadar
ultima formulă esti va fi egal
b13 pe 10 pe lângă 1 minus rația
este 1 pe 10 la puterea n totul
supra 1 minus 1 pe 10 egal cu 3
supra 10 ori aducem la numitor
comun numitorul comun este 10 la
n avem 10 la n minus 1 supra 10
la n totul supra amplificăm 60
cu 10 10 minus 1 9 pe 10 egal cu
3 supra 10 ori 10 la n minus 1
supra 10 la n ori inverse amandoua
fracție 10 pe 9 se simplifică în
10 cu 10 9 cu 3 și obținem 10 la
n minus 1 supra 3 ori 10 la n aceasta
este suma s și acum trebuie să
calculăm s minus 1 pe 3 minus 1
pe 3 va fi egal cu 10 la n minus
1 supra 3 ori 10 la n minus 1 pe
3 aducem 60 la numitor comun amplificăm
cu 10 la n a doua fracție și obținem
10 la n minus 1 minus 10 la n supra
3 ori 10 la n se reduce 10 la n
și obținem în final minus 1 supra
3 ori 10 la puterea n
Proprietațile progresiei geometriceAscunde teorie X
Navigare în lectii
Cumpara abonament
