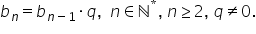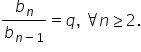Progresii geometrice - noțiuni introductive

elevul Ionel a lipsit de la lecția

a progresiei geometrice și a căutat

pe internet informații despre această

noțiune a descoperit saitul lecții

virtuale și Și a făcut un cont

pe acest site aicea găsi multe

informații utile despre progresii

geometrice dar și despre alte noțiuni

învățate la școală fiind încântat

de acest site la recomandat și

altor doi prieteni a doua zi aceștia

sau înscris pe site și au fost

foarte bucuroși să descopere lecții

video la matematică fizică și chimie

la rândul lor ei au recomandat

saitul altor persoane astfel că

în a treia zi te să am scris patru

elevi în următoarea zi fiecare

dintre aceștia A recomanda saitul

altor 2 iar în a patra zi încă

opt elevi sau înscris pe site dacă

algoritmul ar continua în a cincea

zi se înscrie 16 elevi iar în a

șasea zi 32 dacă scriem aceste

numere pe care le am obținut sub

forma unui șir vom avea șirul 1

2 4 8 16 32 și așa mai departe

în acest șir observăm că fiecare

termen începând cu al doilea se

obține Înmulțind termenul precedent

cu doi unu ori doi este de 2 ori

2 4 în 4 2 8 și așa mai departe

În astfel de șir în care fiecare

termen se obține Înmulțind termenul

precedent cu același număr nenul

se numește progresie geometrică

iar numărul respectiv se numește

rație dacă algoritmul No ar continua

în același mod credeți că am putea

să aflăm Câte persoane se folosire

pe saitul lecții virtuale în 15-a

zi sau Câte persoane sau înscris

în total în cele 15 zile Bineînțeles

că putem și chiar o să calculăm

acest lucru în lecția următoare

până atunci Haideți să mai vedem

câteva exemple de progresii geometrice

prima șir 3 minus șase 12 minus

24 48 și așa mai departe este o

progresie geometrică cu rația egală

cu minus doi la nota rația progresiei

geometrice cu q Așadar în acest

caz q este minus doi în următorul

exemplu avem șirul 1 5 25 125 625

și așa mai departe acesta este

o progresie geometrică având rația

egală cu 5 și în al doilea exemplu

avem progresia 1 pe 3 1 pe 3 la

a doua 1 pe 3 la a treia 1 pe 3

la a patra și așa mai departe Aceasta

este o progresie geometrică având

rația egală cu 1 pe 3 Dacă un șir

bn este progresie geometrică bancnota

acest lucru în felul următor iar

fiecare termen începând cu al doilea

se obține Înmulțind termenul trece

Dent cu același număr nenul Așadar

are loc relația de recurență b

n egal cu b n minus 1 ori q oricare

ar fi n mai mare sau egal cu 2

este număr real nenul iar b 1 adică

primul termen al progresiei este

un număr real fixat spunem Așadar

că o progresie geometrică este

bine determinată dacă se cunoaște

primul termen și rația această

relație de recurență se mai poate

scrie și astfel de n supra b n

minus 1 egal cu q observăm Așadar

că între o progresie geometrică

în raportul la doi termeni consecutivi

este constant adică nu depinde

de an prin urmare Pentru a stabili

dacă un șir e progresie geometrică

verificăm Dacă raportul a doi termeni

consecutivi este constant în continuare

mă face două exerciții simple primul

exercițiu scrie exprimi patru termeni

ai progresiei geometrice b n Dacă

B1 este egal cu 4 și rația este

egală cu 1 pe 2 primul termen este

dat acesta este 4 al doilea termen

se obține Înmulțind primul termen

cu rația egal cu 4 ori 1 pe 2 și

egal cu 2 al treilea termen b 3

se obține Înmulțind termenul precedent

cu rația Deci avem de 2 ori q egal

cu 2 ori 1 pe 2 egal cu 1 și al

patrulea termen va fi egal cu b

3 ori q egal cu 1 ori 1 pe 2 și

1 pe 2 Aceștia sunt primii patru

termeni ai acestei progresii geometrice

și al doilea exercițiu fie șirul

b n unde n este egal cu radical

din 7 8 5 la n Verificați dacă

șirul este progresie geometrică

Pentru a stabili dacă un șir este

progresie geometrică verificăm

Dacă raportul a doi termeni consecutivi

este constant așa dar Haideți să

calculăm raportul b n supra DN

minusu nu acesta va fi egal cu

radical din 7 ori 5 la n supra

radical din 7 ori 5 la n minus

unu se simplifică radical din 7

se simplifică 5 la n cu 5 la n

minus 1 la numărător ne rămâne

cinci Așadar raportul este egal

cu 5 acest număr nu depinde de

an prin urmare raportul la doi

termeni consecutivi este constant

Așadar șirul b n este progresie

geometrică