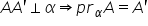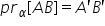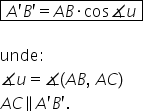Proiecții ortogonale pe un plan
Tag-uri
Partajeaza in Google Classroom

Transcript
să vorbim în continuare despre
proiecții ortogonale Pe plan Ce
înseamnă ortogonal pe scurt ortogonal
înseamnă perpendicular Deci trebuie
să proiectăm în mod perpendicular
pe un plan și ce putem să proiectăm
pe un plan Păi putem să proiectăm
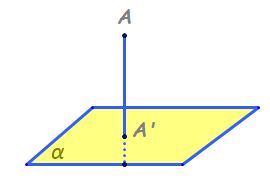
un punct pe un plan Iată vrem să
proiectăm punctul A pe planul alfa
pentru a face acest lucru trebuie
să ducem perpendiculară din acest
punct Pe plan Deci vom trasa O
dreaptă care trece prin a și acea
dreaptă este perpendiculară pe
planul alfa și o să trasez mai
întâi dreapta așa apoi trece în
punctul de intersecție al dreptei
cu planul trecem aici a prim și
facem această parte a dreptei punctat
pentru că ea se află sub plan deci
practic nu se vede Bun și venim
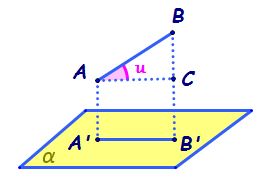
și notăm Care este proiecția punctului
contul lui a pe planul alfa este
chiar punctul de intersecție al
dreptei cu acest plan de ce este
punctul a prim devreme c a prim
este perpendiculară pe Alfa atunci
rezultă că proiecția și vom nota
așa pe aer proiecția punctului
a idee să scriu mai la dreapta
punctului a pe planul alfa și planul
alfa venim și o trecem Aici este
punctul a prim și astfel Am proiectat
un punct pe un plan dacă însă punctul
aparține planului Deci punctul
b este în planul alfa atunci din
acest punct nu avem ce perpendiculară
să ducem pe plan pentru că deja
punctul este în plan Deci dacă
punctul B aparține planului Alfa
înseamnă că proiecția punctului
b pe planul alfa este care credeți
chiar punctul B mult mai putem
să proiectăm și un segment pe un
plan Iată vrem să proiectăm pe
planul alfa segmentul ab atenție
când proiectăm pe un plan puncte
coliniare atunci ceea ce vom obține
vor fi tot puncte coliniare Deci
proiectând un segment pe un plan
homo obține tot un segment și este
suficient să proiectăm capetele
segmentului Deci vom proiecta mai
întâi punctul A pe planul alfa
și voi duce această linie punctată
și avem aici a prim proiecția punctului
a pe planul alfa și apoi proiectăm
punctul B pe planul alfa și obținem
aici punctul d prim proiecția segmentului
a b pe planul alfa este segmentul
a prim b prim și venim aici și
notăm proiecția pe planul alfa
a segmentului AB voi trece aici
pe mentul închis AB este segmentul
închis a prim b prim dacă proiectam
un segment deschis Deci aveam aici
paranteze rotunde obținem tot un
segment deschis Care este legătura
între lungimea segmentului proiectat
și lungimea proiecției Deci legătura
între lungimea segmentului AB și
a segmentului a prim b prim p Pentru
aceasta vom construi o paralelă
prin a la a prim b prim și această
paralelă intersectează segmentul
B B prim în punctul C voi trece
aici punctul C Ce știm iată că
ac este paralelă cu a prim b prim
și devreme c b b prim a perpendiculară
pe planul alfa înseamnă că b d
prim perpendiculară pe a prim b
prim și cum a prim D prim e paralelă
cu a Ce înseamnă că BB prim perpendicular
pe AC De ce avem aici un unghi
de 90 de grade Deci triunghiul
BCA este un triunghi dreptunghic
nu uitați noi vrem să găsim legătura
între AB și a prim b prim Însă
a prim b prim cu c segment este
congruent Păi avem aici să ne uităm
la patrulaterul a c d prim a prim
a a prim și c și c b prim sunt
paralele la fel și a c și a prim
b prim De ce avem aici un paralelogram
chiar mai mult pentru că avem aici
un unghi de 90 de grade înseamnă
că și acest unghi are tot 90 de
grade pentru că punctele b c b
prim sunt coliniare Deci avem de
fapt un dreptunghi Haide să trasezi
aici se vadă mai clar că avem un
unghi drept bun asta înseamnă că
a prim b prim acest segment congruent
cu ac și atunci Care e legătura
între ac și ab Păi avem aici un
triunghi dreptunghic și voi nota
aici cu unghiul făcut de AB și
AC 60 să scriem formula cosinusului
cosinus de unghiul u Cu cât este
egal pe avem lungimea catetei alăturate
unghiului dac trecem aici ace supra
lungimea ipotenuzei adică abc rezultă
de aici rezultă că ac se scrie
ab ori cosinus de unghiul u a b
înmulțit cu cosinus de x dar nu
e am spus că aceeasi segmente concurent
cu a prim b prim devreme c AC este
egal cu a prim b prim rezultă că
a prim b prim lama locuit pe AC
este egal cu a b înmulțit cu cosinus
de unghiul x și chiar putem să
încadrăm această relație și astfel
am găsit legătura între Iată lungimea
segmentului AB și lungimea proiecției
sale a prim b prim dacă însă segmentul
pe care vrem să îl proiectăm este
perpendicular pe plan atunci ce
vom obține Păi trebuie să proiectăm
fiecare punct al segmentului Pe
plan cam spus e suficient să proiectăm
capetele segmentului și acum Dacă
proiectăm punctul C Pe planul gama
Deci din ce trebuie să ducem o
linie punctată nu voi a tras aici
și o voi transa de aici încolo
și vom obține aici si prim proiecția
punctului C Pe planul gama Dacă
proiectăm punctul d Pe planul gama
promo tot punctul c prim deci de
fapt în această situație proiecția
segmentului este de fapt un punct
Deci venim și notăm proiecția Pe
planul gama a segmentului închis
CD este de fapt punctul c prim
atenție însă noi proiectăm aici
o mulțime de puncte mulțimea a
punctelor care alcătuiesc acest
segment Da avem aici o mulțime
de puncte atunci ce vom obține
este tot o mulțime și anume mulțimea
formată din punctul c prim de aceea
trebuie să trecem aici între acolade
acest punct proiecția Pe planul
gama a segmentului închis CD este
mulțimea formată din punctul c
prim o singură observație mai vreau
să facem aici când proiectăm un
segment pe un plan și anume când
proiectăm pe un plan mijlocul unui
segment Deci dacă m este mijlocul
segmentului de Iată uite si aici
de segmentul de congruent cu segmentul
m n atunci proiecția punctului
m Pe planul Beta să notăm aici
obținem punctul M prim proiecția
punctului m Pe planul Beta este
mijlocul proiecției adică D prim
m prim este congruent cu m prim
e prim cu alte cuvinte proiecția
mijlocului este mijlocul proiecției
Deci dacă dm este egal cu m e atunci
rezultă că d prim m prim este egal
cu m prim e prim Evident putem
să trecem aici și eu să folosiți
scrierea cu paranteze Deci vom
folosi scrierea cu segmente și
vom trece congruente la fel și
aici mai putem să proiectăm Udrea
pe un plan dacă dreapta inclusă
în plan atunci proiecția dreptei
Pe plan nici ar dreapta respectivă
dacă însă avem o dreaptă exterioară
unui plan atunci avem trei situații
posibile și anume dreapta este
paralelă cu planul dreapta e paralelă
cu planul alfa și vrem să proiectăm
această dreaptă Pe plan mai des
alegem două puncte pe această dreaptă
a și b și vom proiecta fiecare
punct împarte proiectăm punctul
A și notăm aici a prim proiecția
punctului a pe plan și la fel procedăm
și pentru punctul B trecem aici
B prim proiecția punctului b pe
planul alfa știm deja că atunci
când proiectăm puncte coliniare
obținem tot puncte coliniare Deci
proiectând o dreaptă pe un plan
vom obține tot o dreaptă și anume
dreapta a prim b prim de să notăm
că proiecția dreptei ab pe planul
alfa este dreapta a prim b prim
și cum dreapta a a b este paralelă
cu planul alfa atunci ce am obținut
Aici este o dreaptă paralelă cu
dreapta AB DC AB este paralelă
cu a prim b prim dacă însă dreapta
este perpendiculară pe plan Iată
dreapta d perpendiculară pe planul
alfa atunci dacă alegem punctul
se spune în b pe dreapta d atunci
proiectând punctul B pe planul
alfa a vom obține punctul o la
fel și dacă luăm un punct de sub
plan de exemplu alegem aici punctul
A pe care dacă îl proiectăm pe
planul alfa ne va da tot punctul
O de fapt proiectând orice punct
al dreptei Pe plan vom obține punctul
o adică punctul de intersecție
al dreptei cu planul alfa cu alte
cuvinte proiecția dreptei D pe
planul alfa este mulți A formată
din punctul o m aceasta a se obține
dacă avem o dreaptă perpendiculară
pe plan dacă însă avem o dreaptă
secantă cu planul Iată dreapta
d este secantă planului Alfa atunci
cum obținem proiecția aceste drepte
pe planul alfa Păi mai întâi Haide
să mute acest notația acestui punct
o vom trece aici pentru că o să
avem nevoie de spațiu și să alegem
Pe planul pe dreapta d pardon un
punct de exemplu aleg aici punctul
b și îl proiectez pe planul alfa
și voi obține aici punctul B prim
mine alegem aici încă un punct
să îi spunem si pe care tot așa
îl proiectăm pe același plan și
trecem aici punctul c prim e bine
știm deja că dacă proiectăm puncte
coliniare obținem tot puncte coliniare
Deci ce vom obține este tot o dreaptă
și anume aceasta dreapta pe care
o putem numi Fie AB prim fie a
c prim și c prim b prim Deci proiectând
dreapta de pe planul alfa proiecția
pe planul alfa a dreptei d este
dreapta sau numim c prim b prim
și astfel Am proiectat Pe plan
și o dreaptă secantă cu planul