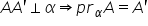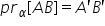Proiecții ortogonale pe un plan. Aplicații.

în continuare să aplicăm în două

exerciții această noțiune de proiecție

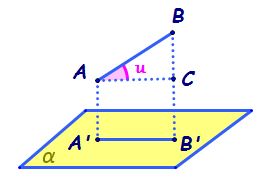
ortogonală pe un plan cine se dă

aici un cub a b c d a prim b prim

c prim D prim și vrei mai întâi

să determinăm proiecția punctului

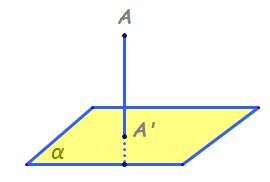
a prim Pe planul abc Iată aici

avem punctul a prim iar planul

abc Hai desfășurăm este acesta

avem aici planul abc Care este

proiecția punctului a prim pe acest

plan pe foarte simplu pentru că

ea a prim a este perpendiculară

pe planul abc Deci notăm a prim

a perpendiculară pe planul ABC

de unde rezultă că proiecția punctului

a pe acest plan este chiar punctul

A Deci ștergem aici trecem că obținem

punctul A 2-a cerință să determinăm

acum proiecția tot Pe planul abc

A segmentului d prim D prim segment

deschis iar segmentul D prim D

prim D prim b prim pardon este

acesta care este proiecția acestui

segment Pe planul abc care de fapt

este unul și același cu planul

a b c d deci putem să prelungim

aici avem unul și același plan

îi proiecția punctului D prim Pe

planul a b c d este chiar punctul

D pentru că d prim D perpendiculară

pe a c splen Deci voi scrie direct

că proiecția punctului D prim Pe

planul a b c d de fapt trebuie

să scrie mai la dreapta Uite ce

doar ABC este de fapt punctul d

iar proiecția punctului b prim

pe același plan a b c este de fapt

b proiectând punctul d prim obținem

punctul d proiectând deprim obținem

punctul B semne că proiectând de

fapt segmentul D prim b prim vom

obține acest segment de B Deci

notăm aici rezultă că din aceste

două relații proiecția acestui

segment deschis Pe planul ABC este

de fapt segmentul deschis b d al

doilea exercițiu este acesta în

care ni se dă dreapta AB perpendiculară

pe planul alfa în i se mai dă Punctul

C care aparține planului Alfa la

fel și punctul B aparține lui Alfa

și vrem să determinăm proiecția

pe planul alfa a punctului b mai

devreme si punctul b este în planul

alfa d și b aparține planului Alfa

are dacă proiecția pe planul alfa

a punctului b este chiar punctul

B următoarea cerință proiecția

punctului a pe planul alfa dacă

proiect în punctul A pe planul

alfa atunci ce punctul vom obține

îi vom obține punctul B pentru

că dreapta a b perpendiculară pe

Alfa d a b perpendiculară pe Alfa

ia avem relația și aici rezultă

că proiecția punctului a pe planul

alfa este punctul B să găsim acum

proiecția dreptei ab pe planul

alfa Deci proiectăm dreapta AB

pe acest plan pe Cum este dreapta

a b față de planul alfa este perpendiculară

pe acest plan Deci dacă a b perpendiculară

pe Alfa atunci ce vom obține Păi

orice punct de pe această dreapta

Am proiectat pe planul alfa Nevada

punctul B adică punctul de intersecție

al dreptei cu planul Deci rezultă

că proiecția pe planul alfa a dreptei

ab este dată de punctul B pe care

atenție îl trecem între acolade

avem aici mulțimea formată din

punctul B pentru că 60 proiectam

o mulțime mulțimea a punctelor

care alcătuiesc dreapta AB altă

cerință să găsim acum proiecția

pe planul alfa a segmentului AB

de Iată segmentul ab însă explicația

este asemănătoare cu cea de aici

pentru că segmentul a b se află

pe dreapta ab care perpendiculară

pe planul alfa Deci proiectând

acest segment Pe plan Nevada tot

punctul B Deci venim aici și șterge

și trecem direct că obține mulțimea

formată din punctul B să găsim

acum proiecția segmentului ac pe

planul alfa Deci proiectăm segmentul

AC pe acest plan pe trebuie să

proiectăm capetele acestui segment

și atunci proiecția punctului a

pe planul alfa Care este proiecția

punctului a pe planul alfa este

dată de punctul B proiecția punctului

C pe planul alfa este chiar punctul

c pentru că ce aparține planului

Păi Ce rezultă de aici că proiecția

pe planul alfa a segmentului ac

este segmentul BC Deci proiecția

pe planul alfa a segmentului închis

AC este de fapt segmentul închis

bc adică acest segment și ultima

întrebare să determinăm proiecția

dreptei a c pe planul alfa Păi

deja aici am stabilit că proiect

în punctul A pe planul alfa obținem

punctul b proiectând punctul C

pe planul alfa ne dă punctul C

Deci proiectând dreapta a c pe

planul alfa a vom obține Iată dreapta

b c sau ce becul vrei să îi spunem

ștergem aici și trecem dreapta

b c