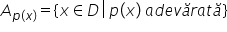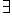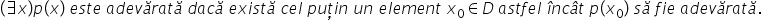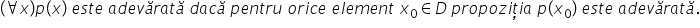Propoziții, predicate și cuantificatori

această lecție va deschide un nou

capitol numit elemente de logică

matematică și teoria mulțimilor

logica studiază propozițiile însă

nu din punct de vedere gramatical

pe noi la matematică ne interesează

doar valoarea lor de adevăr prin

urmare logica matematică studiază

accele enunțuri care pot fi adevărate

sau false iar un astfel de enunț

se numește propoziția acest capitol

își propune să consolideze limbajul

și raționamentul matematic iar

în lecția aceasta o să discutăm

despre propoziții predicate și

cuantificatori să ne uităm puțin

la aceste enunțuri și să vedem

care dintre acestea sunt propoziții

primul enunț Cât e ceasul nu este

o propoziție matematică pentru

că nu putem spune cu certitudine

că ea este adevărată sau falsă

prin urmare aceste nunți nu este

o propoziție partea întreagă a

numărului 3 este 3 este o propoziție

adevărată Închide ușa Nu este o

propoziție enunțurile imperative

și interogative nu sunt propoziții

matematice x plus 7 egal 11 unde

x este număr real acest enunț ar

putea fi o propoziție adevărată

pentru o anumită valoare a lui

x însă pentru alte valori ale variabilei

x poate fi o propoziție falsă prin

urmare nu putem ști cu certitudine

dacă este adevărat sau fals acest

enunț înseamnă că nu este o propoziție

5 mai mare decât 9 este o propoziție

falsă dreptunghiul are toate unghiurile

drepte este o propoziție adevărată

și doi plus 10 egal 9 este o propoziție

falsă propozițiile se pot nota

cu litere mici litere notăm această

propoziție cu p a doua cu q r și

s prima luarea de adevăr a unei

propoziții înțelege în proprietatea

acesteia de a fi adevărată sau

falsă valoarea de adevăr a unei

propoziții se notează astfel și

a poate fi egală cu unu dacă p

este adevărată sau 0 dacă p este

falsă în lung de 1 și 0 putem pune

și simbolurile A și F de la adevărat

sau fals și acum să vedem ce valoare

de adevăr are prima propoziție

partea întreagă a numărului 3 este

3 spuneam că aceasta este o propoziție

adevărată și atunci valoarea sa

de adevăr va fi 1 valoarea de adevăr

a propoziției q este 0 pentru că

am spus că această propoziție este

falsă valoarea de adevăr a propoziției

a r dreptunghiul are toate unghiurile

drepte este egală cu 1 și valoarea

de adevăr a propoziției s 2 plus

10 egal 9 este propoziția falsă

Deci valoarea de adevăr este egală

cu 0 acum să ne îndreptăm atenția

asupra acestui enunț spuneam mai

devreme că pentru o anumită valoare

atribuită variabilei x putem obține

o propozitie adevărată iar pentru

alte valori obținem o propoziție

falsă un astfel de enunț în care

apare una sau mai multe variabile

se numește predicat să vedem în

continuare și alte exemple de predicate

predicatele se notează cu p mic

iar în paranteză se trece variabila

care apare în enunț Primul predicat

pdx x plus 5 mai mic decât 10 unde

x este număr real pentru că în

aceste nunți apare o singură variabilă

acest predicat se va numi predicat

Un ar al doilea predicat este un

predicat venal deoarece aici Avem

două variabile în enunț x plus

y egal 7 unde x și y sunt numere

naturale al treilea predicat este

un predicat Turner pentru că avem

trei variabile x pătrat plus pătrat

egal cu Z pătrat unde x y și z

sunt numere naturale dacă atribuim

variabilelor anumite valori obținem

propoziții adevărate sau false

să ne uităm la Primul predicat

și să vedem ce propoziție obținem

pentru x egal cu unu obținem următoarea

propoziție pe DN1 1 plus 5 mai

mic decât 10 aceasta este propoziție

adevărată în al doilea predicat

monta variabilelor x și y valorile

1 și 2 obținem astfel propoziția

pe de 1 și 2 1 plus 2 este egal

cu 7 Aceasta este o propozitie

falsă și pentru al treilea predicat

să vedem ce propoziții obținem

în cazul în care x este 1 este

2 și z este 3 obținem astfel că

1 la pătrat plus 2 la pătrat este

egal cu 3 la pătrat 5 egal cu 9

este o propoziție falsă și acum

să vedem ce propoziții obținem

dacă x este 3 4 și Z5 e de 3 4

5 3 la pătrat plus 4 la pătrat

egal cu 5 la pătrat Aceasta este

o propoziție adevărată pentru că

numerele 3 4 și 5 sunt numere pitagorice

observăm Așadar că Pentru anumite

valori atribuite variabilelor predicatele

devin propoziții adevărate ia pentru

alte valori de vin propoziții false

această mulțime care apare aici

se numește mulțimea de valori sau

domeniul de definiție al predicatului

pentru predicatul unr domeniul

de definiție este r în acest caz

în al doilea exemplu domeniul de

definiție este l iar în al treilea

exemplu domeniul de definiție a

creditului este n în continuare

să vedem Ce înțelegem prin mulțimea

de adevăr a un predicat am notat

această mulțime cu A mare de la

adevăr mulțimea de adevăr a predicatului

p de x este formată din acele elemente

x din domeniu a notat cu Denis

este meniu cu proprietatea că p

de x este o propoziție adevărată

și în continuare un exemplu concret

avem următorul predicat pe Dan

x x plus 4 supra x plus 5 este

număr întreg unde x este număr

întreg diferit de minus 5 ne propunem

să determinăm mulțimea de adevăr

a acestui predicat mai exact trebuie

să vedem Pentru ce valori ale variabilei

x fracția aceasta este număr întreg

o să mai scriu o dată x plus 4

supra x plus 5 o fracție este număr

întreg dacă numărătorul se împarte

exact la numitor sau altfel zis

dacă numitorul este un divizor

al numărătorului dar ajutat dacă

locul expresiei de la numărător

am avea un număr pentru că atunci

am putea să scriem divizorii acelui

număr și atunci mă faci un artificiu

de calcul în loc de patru o să

scriem cinci minus 1 și o să vedeți

imediat de ce așa Dar avem x plus

5 minus 1 supra x plus 5 la numărător

avem o diferență și atunci putem

să despărțim această fracție în

alte două fracții prima fracție

x plus 5 supra x plus 5 minus 1

supra x plus 5 Observați că se

simplifică x plus 5 acesta este

și motivul pentru care am vrut

să le scriem pe 4 cu ajutorul lui

cinci și obținem în continuare

egal cu 1 minus 1 supra x plus

5 din moment ce 1 este număr întreg

pentru ca toată această expresie

să fie număr întreg mai trebuie

ca fracția aceasta să fie număr

întreg 1 supra x plus 5 este număr

întreg dacă x plus 5 este un divizor

al lui 1 prin urmare x plus 5 aparține

mulțimii formate din elementele

1 și minus 1 Aceștia sunt divizorii

lui 1 vorbind despre divizori întregi

în continuare Nu ne rămâne decât

să rezolvăm aceste Două ecuații

prima ecuație x plus 5 egal cu

1 va avea soluția x egal cu minus

4 x plus 5 egal cu minus unu are

soluția x egal cu minus 6 deci

pentru aceste două valori atribuite

variabilei x fracția noastră este

număr întreg Deci mulțimea de adevăr

acestui predicat este a mare formată

din elementele minus 4 și minus

6 spuneam mai devreme că dacă atribuind

variabilelor anumite valori transformăm

predicatele în propoziții însă

mai avem și o altă metodă de a

transforma predicatele în propoziții

folosind anumite expresii să vedem

în continuare Care sunt aceste

expresii prin care putem transforma

un predicat în propoziție folosind

expresia există cel puțin un x

astfel încât să aibă loc pe de

x transformăm un predicat în propoziție

iar această propoziție se numește

propoziția existențială Și a se

notează astfel există cel puțin

un x astfel încât să aibă loc pe

de x sau mai putem nota așa există

x un număr din domeniu astfel încât

are loc propoziția pe de x acest

simbol ca și un e întors se citește

există și se numește cuantificatori

existențial moartea expresii cu

ajutorul căruia putem transforma

în predicat între o propoziție

este următoarea expresie oricare

ar fi x are loc pe de x această

expresie transformăm predicat în

propoziție iar această propoziție

se numește propoziție universală

și se notează astfel oricare ar

fi x are loc pe dx sau mai poate

fi notată și așa oricare ar fi

x un element din domeniul de definiție

are loc pe de x acest simbol se

citește oricare ar fi și se numește

cuantificator universal Propoziția

existențială este adevărată dacă

există cel puțin un element x din

domeniul de Valori astfel încât

propoziția pdx să fie adevărată

iar propoziția universală este

adevărată dacă pentru orice număr

x din domeniul de Valori pdx este

adevărată în schimb propoziția

universală este falsă dacă există

cel puțin un x din mulțimea de

Valori astfel încât p de x să fie

falsă să vedem în continuare un

exemplu concret pornind de la acest

predicat pdx x divide pe 8 unde

x este număr natural să construim

propoziția existențială propoziția

universală și să vedem apoi valoarea

de adevăr a acestora începem cu

propoziția existențială există

un x număr natural astfel încât

x divide pe opt sau mai putem să

notăm și așa există x un element

din mulțimea numerelor naturale

astfel încât x divide pe opt spuneam

că propoziția existențială este

adevărată dacă există cel puțin

un element din domeniul de Valori

adică azul nostru din n astfel

încât x cel dividă pe 8 de exemplu

pentru x egal cu 2 această relație

de divizibilitate este adevărată

Așadar Propoziția existențială

este propoziția adevărată este

suficient să găsim cel puțin o

valoare a lui x astfel încât relația

aceasta să aibă loc pornind apoi

de la acest predicat să construim

propoziția universală oricare ar

fi x număr natural x divide pe

8 sau oricare ar fi x număr natural

x divide pe 8 cazul în care există

cel puțin un număr natural pentru

care această relație să nu aibă

loc propoziția universală va fi

falsă ne exemplu pentru x egal

cu 9 9 divide pe opt este o propoziție

falsă înseamnă că această relație

de divizibilitate nu are loc pentru

orice număr natural prin urmare

propoziția universală este falsă

nu mai facem în continuare niște

aplicații Fie x un număr întreg

și ne propunem să vedem valoarea

de adevăr a acestor propoziții

prima propoziție există x număr

întreg astfel încât modul din 4

minus x plus modul din 2x minus

8 să fie egal cu 0 dacă găsim cel

puțin unul număr întreg astfel

încât această egalitate să aibă

loc atunci Propoziția este adevărată

Suma a două module este 0 Dacă

fiecare dintre aceste două module

este egal cu 0 modul din 4 minus

x este 0 dacă x este egal cu 4

iar modul din 2x minus 8 este 0

dacă x este egal cu 4 primare am

găsit cel puțin o valoare a lui

x astfel încât această relație

să fie adevărată prin urmare această

propoziție este o propoziție adevărată

a doua propoziție oricare ar fi

x număr întreg 2x minus opt este

mai mare sau egal decât 0 trebuie

să vedem dacă această relație are

loc pentru orice număr întreg sau

să găsim cel puțin un număr întreg

pentru care inegalitatea este falsă

De exemplu dacă x este egal cu

unu obținem 2 minus 8 Adică min

6 mai mare sau egal decât 0 Adică

o propoziție falsă având în vedere

că am găsit cel puțin o valoare

a lui x pentru care această inegalitate

este falsă propoziția oricare ar

fi x 2x minus 8 mai mare sau egal

decât 0 este o propoziție falsă

a treia propoziție există x număr

întreg astfel încât x la a doua

minus 64 egal cu 0 să vedem dacă

găsim cel puțin un x pentru care

să aibă loc egalitatea aceasta

există chiar două valori pentru

x și anume X1 egal cu 8 și X2 egal

cu minus opt pentru aceste două

valori ale lui x egal litatea aceasta

este adevărată Deci Propoziția

existențială este adevărată în

cazul în care avem predicate binare

sau ternare acesteia pot fi transformate

în propoziții utilizând cu anticarul

existențial în combinație cu cel

universal de exemplu avem aceste

ridicat binar 3 x plus y egal cu

1 unde x și y sunt numere întregi

putem transforma acest predicat

în propoziție folosind cei doi

cuantificatori de exemplu putem

obține propoziția oricare ar fi

x există un yn300 lângă 3 x plus

y să fie egal cu 1 sau o altă propoziție

există x număr întreg astfel încât

oricare ar fi Y apartamente cu

edificator nu sunt comutative pentru

că aceste două propoziții număr

avea aceeași valoare de adevăr

o să vedem imediat de ce să determinăm

mai întâi valoarea de adevăr a

acestei propoziții sau mai citim

odată pentru orice x număr întreg

există un y9 întreg astfel încât

3 x plus igrec să fie egal cu 1

Haideți atunci să ne alegem un

x arbitrar ești pentru un x număr

întreg ales arbitrar trebuie să

verificăm dacă există cel puțin

un y7 această egalitate să aibă

loc dacă îl exprimăm pe ecran din

această relație avem că y este

egal cu 1 minus 3x Deci pentru

un x ales arbitrar există trei

adevărul ytmp3 ca aceasta să aibă

loc însă nu este suficient să le

exprimăm pe ia din această relație

trebuie și să verificăm dacă acesta

este număr întreg din moment ce

x ia doar valori întregi atunci

și y a fi număr întreg pentru că

nu există aici pericolul să avem

vreo fracție sau lângă radical

Așadar y scrise sub această formă

este număr întreg Deci această

propoziție este propoziție adevărată

întrucât x a fost ales arbitrar

Deci oricare ar fi x din sat există

una din z astfel încât 3 x plus

igrec să fie egal cu unu în a doua

propoziție trebuie să verificăm

dacă există cel puțin un x număr

întreg astfel încât oricare ar

fi Y apartamente Vaslui x Haideți

să exprimăm pe x x va fi egal cu

1 minus y supra 3 trebuie să vedem

dacă acest x este număr întreg

pentru orice valoare a lui y din

z însă dacă alegem pe y2 Gal cu

2 obținem că x este egal cu minus

1 supra 3 dar minus 1 supra 3 nu

este număr întreg prin urmare nu

pentru orice număr din Zet există

un x astfel încât 3 x plus y să

fie egal cu 1 Deci această propoziție

este falsă rețineți Așadar că cei

doi cuantificatori nu sunt comutative

în concluzie Voi trebuie să rețineți

din această lecție următoarele

aspecte o propoziție este un enunț

care poate fi adevărat sau fals

un predicat este un enunț care

conține una sau mai multe variabile

și Pentru anumite valori atribuite

variabilelor obținem propoziții

adevărate sau false și mai trebuie

să știți că logica matematică are

două principii de bază primul este

principiul tertului exclus asta

înseamnă că o propoziție poate

să fie ori adevărată ori falsă

a treia variantă nu există și mai

avem principiul noncontradicției

Adică o propoziție nu poate să

fie în același timp și adevărată

și falsă cam atât gata