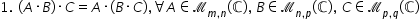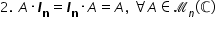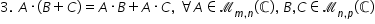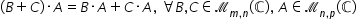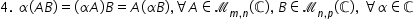Proprietăți ale înmulțirii matricelor

ceasul știi ce proprietăți are

această operație să vedem dacă

înmulțirea matricelor este o operație

comutativă dacă ne referim la matricele

de mai sus matricea a este de tipul

3 2 matricea b este de tipul 2

3 ceea ce înseamnă că se poate

efectua și operația pe ora pentru

calculul matricei b ora vom scrie

explicit matricele b respectiv

a minus 1 4 0 3 minus 2 minus 3

înmulțit cu matricea 1 2 minus

2 0 4 minus 1 și înmulțim în același

mod liniile matricei b cu coloanele

matricei a obținem Așadar matricea

A minus 1 ori 1 plus 4 ori minus

2 plus 0 ori 4 minus 1 ori 2 plus

4 ori 0 plus 0 ori minus unu pentru

linia a doua efectuăm calculele

3 ori 1 plus minus 2 ori 2 plus

minus 3 ori 4 3 înmulțit cu 2 plus

minus 2 înmulțit cu 0 plus minus

3 înmulțit cu minus unu adică matricea

a minus 1 minus 8 plus 0 minus

2 plus zero plus 0 3 plus 4 minus

12 6 plus 0 plus 3 adică matricea

minus 9 minus 2 minus 5 și 9 observăm

că matricea A ori B este diferită

de matricea de ora nefiind nici

măcar de același tip chiar dacă

cele două Matrice aur b și b o

rea sunt de același taxe stă situații

în care ele sunt diferite după

cum există situații în care nici

nu se poate efectua înmulțirea

Spre exemplu dacă matricea a ar

fi fost de tipul 2 3 iar matricea

b ar fi fost de tipul 3 4 matricea

a orbi ar fi fost de tipul 2 patru

iar produsul de aur ea nu se poate

efectua pentru că matricea b are

patru coloane iar matricea a are

două linii în concluzie înmulțirea

matricelor nu este o operație comutativă

să studiem acum dacă înmulțirea

matricelor este o operație asociativă

Se consideră matricele a b și c

pătratice de ordinul doi să calculăm

pentru început produsul Laur b

iar rezultatul îl vom înmulțit

cu matricea înmulțim liniile matricei

a cu coloanele matricei pe adică

a ori a plus b ori c a ori a plus

b ori c ori e plus b ori c ori

e plus de aur Cash înmulțit cu

matricea m n p q înmulțim acum

elementele produsului aur b cu

coloanele matricei c a e m plus

b g m plus sa pe Luis bhp a plus

b g n plus afq plus b h q c e m

plus DJ m plus c f p plus d h p

c d j n plus c plus d h q să vedem

acum Ce rezultat obținem la înmulțirea

matricii va cu produsul de orice

înmulțim matricea a b c d cu matricea

e ori în plus f p e m plus s q

j m plus HP gen8 adică a e m plus

a plus b c plus D plus b HP linia

1 coloana a 2-a plus a plus b si

in plus pe HQ înmulțim acum linia

a doua cu coloana 1 adică ce e

m plus c f p plus dgm SP linia

a doua coloana a doua ce e n plus

c f q plus desen plus dhq comparând

acum cele două Matrice constatăm

că acestea sunt egale deci matricele

sunt egale avem astfel egalitatea

a înmulțit cu B totul înmulțit

cu c este egal cu a înmulțit cu

b înmulțit cu c dacă înlocuim acum

matricile a b și c oricare alte

Matrice Cu condiția ca înmulțiri

a să poată fi efectuată egalitatea

se păstrează Așadar înmulțirea

matricelor este o operație asociativă

putem formula acum proprietatea

pe 1 matricea a înmulțită cu matricea

de totul înmulțit cu matricea Ce

este egal cu produsul dintre matricea

a și produsul dintre matricele

d și c Oricare ar fi matricea a

de tipul m n matricea de tipul

NP și matricea si de tipul pe q

știind că operația de înmulțire

a numerelor complexe are ca element

neutru numărul 1 Oare operația

de înmulțire a matricelor ar putea

admite un element neutru fie o

matrice a de tipul m n o matrice

care să poată fi înmulțită la stânga

lui ar trebui să aibă m coloane

iar o matrice care să poată fi

înmulțite la dreapta lui Ioan ar

trebui să aibă în linii să notăm

cu e matricea element neutru ar

trebui să fie o matrice de tipul

n m un element neutru are proprietatea

că înmulțit la stânga și la dreapta

a cu matricea a Îl lasă neschimbat

adică a înmulțit cu ei ar trebui

să fie egal cu e în cu a c egal

cu a pentru orice Matrice a de

tipul MN cu matricea a este de

tipul MN și matricea i se de tipul

n m de tuse că produsul aurie este

o matrice de tipul m m cu matricea

a este de tipul n m și matricea

a este de tipul MN de ducem că

produsul eu ori este o matrice

de tipul n n cele două Matrice

A E respectiv va trebuie să fie

egal cu matricea a astfel obținem

egalitatea că m trebuie să fie

egal cu n în concluzie un posibil

element neutru trebuie să fie o

matrice pătratică de ordin n dar

și matricele pentru care ne punem

problema existenței elementului

neutru trebuie să fie pătratice

de ordin n Dar ce matrici ar putea

juca rolul elementului neutru iau

Matrice pătratică de ordinul 2

cu elementele 1 2 3 4 că Toma matricei

care să joace rolul elementului

neutru de formă a b c d efectuând

produsul aurie înmulțim liniile

matricei a cu coloanele matricei

b obținând matricea a plus doi

c b plus 2-d 3-a plus 4 C respectiv

3 b plus 4 d care Matrice trebuie

să fie egală cu matricea a doua

Matrice sunt egale dacă elementele

corespunzătoare sunt egale obținem

astfel egalitățile a plus doi c

este egal cu unu respectiv Trei

A plus 4 c este egal cu 3 Rezolvând

acest sistem prin metoda reducerii

puteam înmulții prima ecuație cu

minus doi reducând necunoscuta

si obținem necunoscuta a ca fiind

egală cu unu înlocuind acum această

valoare în prima ecuație în obținerea

si pe c egal cu zero similar obținem

egalitățile b plus 2 d este egal

cu 2 respectiv 3 b plus 4 d este

egal cu 4 Rezolvând acum sistemul

Tot prin metoda reducerii Înmulțind

prima ecuație cu minus 2 adunând

Cele Două ecuații obținute obținem

necunoscute B ca fiind egală cu

zero înlocuind dotă asemenea în

prima ecuație obținem ecuația 0

plus 2 egal cu 2 care ne oferă

și PD Așadar obținem matricea e

ca fiind egală cu matricea 1 0

0 1 azi putea verifica dacă produsul

a înmulțit cu a este egal tot cu

ei Dacă înlocuim acum matricea

a oricare alta Matrice pătratică

de ordinul 2 obținem ca un posibil

element neutru tot această Matrice

Așadar matricea care joacă rolul

elementului neutru la înmulțirea

matricelor patratice este această

Matrice matricea care are pe prima

diagonală 1 iar în rest zerouri

matricea aceasta o notăm cu e 2

e 2 pentru că este de ordinul 2

și o numim matrice unitate sau

Matrice identică de ordinul doi

dacă vorbim de Matrice pătratică

de ordinul trei e ia are această

formă unul pe prima diagonală și

zerouri în rest aceasta este matricea

unitate de ordinul patru și aceasta

este matricea unitate de ordinul

n Așadar avem proprietatea pe 2

matricea a înmulțită cu matricea

en este egală cu matricea en er

matricea a și egal cu matricea

a Oricare ar fi matricea a o matrice

pătratică de ordinul n știm deja

că există o proprietate de legătură

între adunarea și înmulțirea numerelor

reale adică x înmulțit cu y plus

z este egal cu x ori y plus x y

z oricare ar fi x y z numere reale

este vorba de distributivitate

a înmulțirii orale față de Adunarea

numerelor reale Oare există o proprietate

similară și pentru Matrice Să considerăm

trei Matrice patratice de ordinul

doi cu elemente din mulțimea numerelor

reale Să calculăm matricea a înmulțit

cu suma dintre matricea b și matricea

ce adică matricea a înmulțită cu

unu plus doi zero plus minus unu

trei plus minus unu patru plus

trei palma mulți acum liniile matricei

a cu coloanele matricei b plus

c adică matricea a înmulțită cu

matricea 3 minus 1 2 7 9 mulți

acum liniile matricei a cu coloanele

matricei pe plus c 2 înmulțit cu

3 plus 1 înmulțit cu 2 2 înmulțit

cu minus 1 plus 1 înmulțit cu 7

minus 1 înmulțit cu 3 plus 2 înmulțit

cu 2 minus 1 înmulțit cu minus

1 plus 2 înmulțit cu 7 adică matricea

6 plus 2 minus 2 plus 7 minus 3

plus 4 1 plus 14 obținem Așadar

matricea 8 5 115 să calculăm acum

matricea a înmulțit cu B plus a

înmulțit cu ce adică înmulțim liniile

matricei a cu coloanele matricei

b 2 ori 1 plus 1 ori 3 linia 1

coloana 2 2 ore 0 plus 1 ori 4

linia 2 coloana 1 minus 1 ori 1

plus 2 ori 3 linia 2 coloana A

2-a minus unu vor 0 plus 2 ori

4 plus înmulțim acum liniile matricei

a cu coloanele matricei Si 2 ori

2 plus 1 ori minus 1 2 ori minus

1 plus 1 ori 3 linia 2 coloana

1 minus 1 ori 2 plus 2 ori minus

unu linia 2 coloana A 2-a minus

1 ori minus 1 plus 2 ori 3 adică

efectuând calculele 2 plus 3 plus

4 minus 1 plus șase zero plus opt

plus matricea 4 minus 1 minus 2

plus 3 minus 2 minus 2 1 plus 6

adică avem matricea și în 4 5 8

adunată cu matricea trei unu minus

4 7 obținem Așadar matricea 8 5

115 comparând acum cele două Matrice

observăm că ele sunt egale obținând

Așadar relația a înmulțit cu b

plus c este egal cu a înmulțit

cu B plus a înmulțit cu c aceasta

egalitate poate fi generalizată

formulând proprietatea trei A înmulțit

cu b plus c este egal cu a înmulțit

cu B plus înmulțit cu ce Oricare

ar fi matricea a de tipul m n și

oricare ar fi matricele b și c

de tipul NP dar și relația b plus

c înmulțit cu a este egal cu b

ori a plus c ori a oricare ar fi

matricile b și c de tipul m n și

Oricare ar fi matricea a de tipul

n p putem vorbi așa dar de distributivitatea

la stânga a înmulțirii față de

adunare a matricelor Taci de distributivitatea

la dreapta a înmulțirii față de

adunare a matricelor Ce legături

ar putea exista între înmulțirea

matricelor și înmulțirea matricelor

cu scalari dacă ne referim la matricile

a și b precedente Alfa înmulțit

cu produsul a ori b este egal cu

matricea a o b o avem aici este

egal cu 5 Alpha 4 Alpha 5-alfa

Octav calculând acum alfa o rea

înmulțit cu matricea B Alfa ori

a înmulțim elementele matricei

a cu alfa adică 2 Alpha Alpha minus

Alpha 2L fă înmulțit cu matricea

b103 4 înmulțim elementele matricei

Alfa b coloanele matricei b adică

2 Alpha plus 3 Alfa linia 1 coloana

2 2 Alfa aur zero zero Alfa ori

4 4 Alpha minus Alpha 1 minus Alpha

2L Faur 3 6 Alfa minus Alfa ori

0:02 Alfa ore patru opt ani Adică

matricea 5 Alpha 4 Alpha 5 Alfa

și Dacă vom calcula acum și matricea

a înmulțit cu matricea alfabet

înseamnă să înmulțim matricea 2

1 minus 1 doi ca matricea alfabet

adică Alpha 0 3 Alpha 4 Alpha înmulțim

liniile matricei a cu coloanele

matricei alfabet și obține matricea

i2 Alfa plus 3 Alpha 2.00 plus

1 ori 4 Alpha 4 Alpha minus 1 ori

Alpha minus Alpha 2 ori 3 Alpha

6 alfamino sonor 0 0 2 ori 4 Alpha

8 Adică matricea 5 Alpha 4 Alpha

5-alfa opta să observăm că Alfa

ori matricea a or b este egală

cu matricea alfa a înmulțită cu

b și este egală cu matricea a înmulțită

cu matricea alfabet calitate care

se păstrează și în cazul în care

înlocui matricele a b cu oricare

altă Matrice pentru care mulțimea

Este posibilă putem formula a patra

proprietate pe 4 și anume Alfa

înmulțită cu produsul a ori b este

egal cu a Alfa ori a înmulțit cu

matricea a b și este egal cu matricea

a înmulțit cu produsul Alfred a

Oricare ar fi a o matrice de tipul

m n b o matrice de tipul n p și

Alfa un număr complex