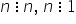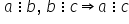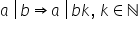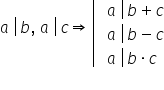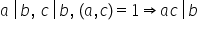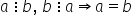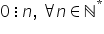Proprietăţi ale relaţiei de divizibilitate în N
Tag-uri
Partajeaza in Google Classroom
Transcript
prima proprietate orice număr natural
se divide cu 1 și cu el însuși
Adică dacă avem un număr a mic
a va fi divizibil cu 1 și a fi
divizibil cu a o definiție foarte
importantă un număr natural mai
mare ca 1 se numește număr prim
dacă se divide numai cu 1 și cu
el însuși Adică are exact doi divizori
suntem câteva exemple doi trei
5 7 13 și așa mai departe primul
număr prim Este 2 și el este și
singurul număr prim par în continuare
să vedem a doua proprietate a relației
de divizibilitate o să începem
cu un exemplu numărul 30 se poate
scrie 10 ori 3 înseamnă că 30 este
divizibil cu 10 numărul 10 se poate
scrie 2 ori 5 înseamnă că 10 este
divizibil cu 2 numărul 30 Putem
să scriem atunci în locul lui 10
îmi scrie 2 ori 5 totul înmulțit
cu trei de oarece înmulțirea este
comutativă putem și asociativă
putem să desfacem parantezele și
acum vom înmulții ultimii doi factori
egal cu 2 ori 15 de unde rezultă
că 30 ma fie divizibil cu 2 Adică
dacă 30 de divizibil cu 10 și 10
divizibil cu 2 înseamnă că 30 va
fi divizibil și cu doi această
proprietate se mai numește și tranzitivitatea
relației de divizibilitate care
poate fi scris astfel Fie a b și
c trei numere naturale dacă a este
divizibil cu b și b divizibil cu
c atunci a este divizibil cu c
în continuare trecem la proprietatea
a treia numărul 6 se scrie trei
ori doi înseamnă că 3 divide pe
6 să scriem în continuare câțiva
multiplii ai numărului 6 următorul
multiplu al lui 6 este 12 12 se
scrie trei ori patru înseamnă că
3 divide și pe 12 dar 12 poate
fi scris de asemenea șase ori doi
înseamnă că trei divide și pe șase
ori doi următorul multiplu este
18 18 înseamnă 3 ori 6 înseamnă
că 3 divide pe 18 18 se mai scrie
și șase ori trei înseamnă că 3
divide și pe 6 ori 3 următorul
multiplu este 24 Care poate fi
scris 3 ori 8 înseamnă că 3 divide
și pe 24 24 poate fi scris șase
ori patru înseamnă că 3 divide
și pe 6 ori 4 și așa mai departe
veți observa că trei divide toate
numerele de forma 6 ori ca un de
cai este un număr natural această
proprietate poate fi scrisă astfel
Fie a și b două numere naturale
dacă a divide pe b atunci a divide
b ori k oricare ar fi k un număr
natural continuăm cu 4-a proprietate
de exemplu numărul 10 se scrie
cinci ori doi înseamnă că 5 divide
pe 10 numărul 15 se scrie cinci
ori trei înseamnă că 5 divide pe
15 Haideți acum să adunăm aceste
două numere 10 plus 15 este egal
cu 25 dar 25 se scrie cinci ori
cinci înseamnă că 5 divide și pe
25 această proprietate poate fi
enunțată astfel Fie a și b două
numere naturale dacă a divide pe
b și a divide pe c atunci a divide
pe b plus c și ultima proprietate
a relației de divizibilitate numărul
63 poate fi scris șapte ori nouă
înseamnă că 7 divide pe 6363 poate
fi scris și trei ori 21 de unde
rezultă că 3 divide pe 63 Dar numărul
63 poate fi scris și 21 ori 3 înseamnă
că 21 divide pe 63 Dar numărul
21 este tocmai produsul numerelor
șapte și trei de unde rezultă că
7 ori 3 divide pe 63 această proprietate
poate fi enunțată astfel Fie a
b și c trei numere naturale dacă
a divide pe b c divide pe b și
numerele a și c sunt prime între
ele atunci produsul aur si divide
pe b
Proprietățile relației de divizibilitateAscunde teorie X
Navigare în lectii
Cumpara abonament
