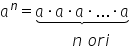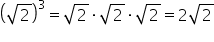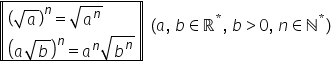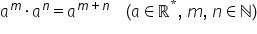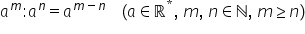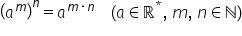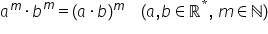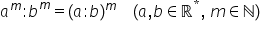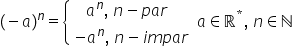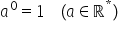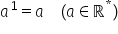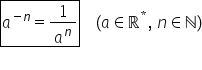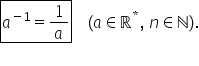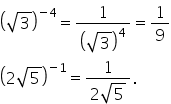Puterea cu exponent întreg a unui numar real
Tag-uri
Partajeaza in Google Classroom

Transcript
Fie a un număr real prin definiție
a la puterea n este produsul a
ori a ori a de n ori de exemplu
radical din 3 la puterea a doua
va fi egal cu radical din 3 ori
radical din 3 care este egal cu
radical din 3 ori 3 egal cu radical
din 9 egal cu 3 radical din 3 este
baza iar 2 se numește exponent
un alt exemplu radical din 2 la
puterea a treia este egal cu radical
din 2 înmulțit cu el însuși de
trei ori radical din 2 ori radical
din 2 este radical din 4 iar adica
din patru este 2 rezultatul va
fi 2 radical din 2 în continuare
să deducem câteva reguli de calcul
cu puteri Fie a și b două numere
reale diferite de 0 ne propunem
să calculăm Ana treia ori a la
a doua mai exact să găsim o regulă
Generală de calcul atunci când
trebuie să înmulțim două puteri
cu aceeași bază ne interesează
să vedem care va fi exponentul
rezultatului ala a treia conform
definiției este a a a iar a la
a doua este a ori a observăm că
factorul a apare de cinci ori în
această înmulțire scrie egal cu
a la a cincea dacă ne uităm acum
la exponenți observăm că exponentul
rezultatului este suma celor doi
exponenți și atunci putem să tragem
următoarea concluzie A la puterea
M ori a la puterea n va fi egal
cu a la puterea m plus n un al
doilea exemplu să vedem ce se întâmplă
cu exponentul rezultatului în cazul
în care avem o împărțire de două
puteri cu aceeași bază împărțirea
știind că se mai poate scrie și
sub formă de fracție și atunci
vom scrie a la a 3-a supra a la
a doua dar ala a treia este a ori
a ori A iar a la a doua este a
ori a putem simplifica cu factorul
a deoarece apare atât la numitor
cât și la numărător și obținem
rezultatul a la puterea Anglia
Care este egal cu a deci exponentul
rezultatului este diferența dintre
cei doi exponenți Și atunci vom
scrie următoarea regulă a la puterea
m împărțit la a la puterea n va
fi egal cu a la puterea M minus
n în cazul în care m este egal
cu n avem a la m împărțit la a
la m Care va fi egal cu a la puterea
M minus m conform acestei reguli
Dar m minus m este 0 Deci obținem
a la puterea 0 atunci când împărțim
un număr la el însuși rezultatul
lui este întotdeauna unu și atunci
putem să tragem următoarea concluzie
Orice număr real a ridicat la puterea
0 va fi în în cazul în care m este
mai mic decât n avem următorul
exemplu a doua împărțit la a la
a treia va fi egal conform acestei
reguli de mai sus a la puterea
2 minus 3 adică a la puterea minus
1 însă ala a doua împărțit la a
la a treia se poate scrie la fel
sub formă de fracție și obținem
a ori a supra a ori a ori a se
simplifică cu a la numărător rămâne
1 iar la numitor avem a putem să
egalăm aceste două relații și să
tragem următoarea concluzie a la
puterea minus 1 este egal cu 1
supra a să mai facem un exemplu
a la a doua împărțit la a la a
patra va fi egal cu a la puterea
2 minus 4 adică a la puterea minus
2 lasa ala a doua a împărțit la
a la a patra se poate scrie sub
formă de fracție astfel a ori a
supra a ori a ori a ori a putem
să simplificăm din nou cu ei la
numărător rămâne 1 iar la numitor
avem a ori a Care este egal cu
a la a doua de aici deducem că
a la puterea minus 2 este egal
1 supra a la a doua și tot așa
în continuare vom de duce că a
la puterea minus n va fi egal cu
1 supra a la n de exemplu 10 la
puterea minus 2 egal 1 supra 10
la puterea a doua Adică 1 supra
100 10 la puterea minus 4 marti
egal cu 1 supra 10 la puterea a
patra Care este egal în continuare
cu 1 supra 10.000 puterile cu exponent
negativ au fost introduse pentru
a scrie mai ușor și pentru a avea
o privire de ansamblu asupra numerelor
foarte mici de exemplu diametrul
atomului de hidrogen este egal
cu 1 ori 10 la puterea minus 8 cm
pentru a ne imagina mărimea diametrului
acestui atom facem următoarea comparație
raportul dintre diametrul unui
atom și cel al unei mingi de fotbal
este același cu raportul dintre
diametrul mingii și cel al Pământului
următoarea regulă pe care dorim
să o deducem trei a la a doua totul
la a treia Vrem să vedem ce se
întâmplă cu exponentul rezultatului
în cazul în care avem puterea unei
puteri ala a doua conform definiției
este a ori a totul la puterea a
treia a ori a la a treia înseamnă
acest produs înmulțit cu el însuși
de trei ori Putem să scriem fără
paranteze și obținem a la puterea
a șasea dacă ne uităm la exponentul
rezultatului observăm că este produsul
dintre cei doi exponenți Și atunci
vom scrie următoarea formulă ala
m totul la puterea n este egal
cu a la puterea M ori and a patra
regulă Ana a treia ori b la a treia
să vedem cum se poate scrie produsul
a doua puteri cu același exponent
a la a treia este egal cu a ori
a ori a iar b la a treia este b
ori b ori b putem să desfacem parantezele
și sări aranjăm termenii deoarece
înmulțirea este asociativă și comutativă
și atunci Putem să scriem astfel
a ori b înmulțit cu aur b înmulțit
cu aur b acest lucru va fi egal
conform definiției puterilor cu
aur b la puterea a treia observăm
Așadar că produsul a doua puteri
cu același exponent va fi egal
cu puterea produsului în general
un număr negativ minus a la puterea
n va fi egal cu Ana and Dacă n
este un număr par și minus Ana
and Dacă n este un număr impar
de exemplu minus 2 supra 3 la puterea
a doua a fi egal cu 4 supra 9 pentru
că doi este un exponent par Iar
atunci când ridicăm un număr negativ
la o putere pară rezultatul va
fi pozitiv iar numărul minus 2
supra 3 ridicat la puterea a treia
a fi egal cu minus 8 supra 27 pentru
că 3 este un exponent impar și
semnul minus se păstrează și la
rezultat 2 la a treia este 8 iar
3 la a treia este 27 și ultima
regulă de calcul cu puteri dacă
avem o fracție ridicată la o putere
de exemplu a supra b la puterea
a treia a fi egal cu a supra b
ori a supra b ori a supra b știind
că atunci când înmulțim trei fracții
se înmulțesc numărătorii între
ei și numitorii între ei a ori
a ori a este a treia iar b ori
b ori B este b la a treia în general
putem deduce această regulă a supra
b la orice putere n a fi egal cu
a la n supra b la n merge exponentul
se distribuie și la numărător și
la numitor nu matinale vom face
câteva exerciții în care vom aplica
aceste reguli de calcul cu puteri
mă plimb exercițiu radical din
7 la puterea a opta împărțit la
radical din șapte la puterea a
șasea Matei egal cu radical din
7 la puterea 8 minus șase am văzut
mai devreme că exponenții se scad
în cazul în care avem de împărțit
două puteri cu aceeași bază 8 minus
6 este 2 deci obținem radical din
7 la puterea a doua n este egal
cu radical din 7 ori 7 egal cu
radical din 49 egal cu 7 în general
rețineți că orice radical ridicat
la puterea a doua este acel număr
de sub radical pentru că ridicarea
la putere și extragerea rădăcinii
pătrate sunt două operații inverse
care se anulează una pe cealaltă
al doilea exercițiu 1 supra 10
la puterea a doua moș 1 supra 10
la puterea a treia când înmulțim
două puteri cu aceeași bază exponenții
se adună Deci obține 1 supra 10
la puterea a cincea care va fi
egal cu 1 la 5 Care este 1 supra
10 la a cincea dar în loc să scriem
unul supra 100.000 este mai simplu
să scriem egal cu 10 la puterea
minus 5 3 5 supra 3 la puterea
minus 1 atunci când avem o putere
negativă dezvoltată este 1 supra
acel număr 1 supra 5 supra 3 linia
de fracție înseamnă împărțire Deci
nu scrie 1 împărțit la 5 supra
3 care este egal în continuare
cu 1 ori 3 supra 5 egal cu 3 supra
5 în general Orice fracție la puterea
minus 1 este inversă fracției respective
4 minus trei supra patru la puterea
minus 1 o să omitem această etapă
de mai devreme și o scrie direct
fracția inversată însă semnul acesteia
se păstrează ne și rezultatul va
fi minus 4 supra 3 5 3 supra radical
din 2 la puterea a doua ori radical
din 2 supra 6 la puterea a doua
având în vedere că avem același
exponent Putem să scriem acest
produs astfel 3 supra radical din
2 ori radical din 2 supra 6 totul
la puterea a doua în paranteză
putem să facem niște simplificări
3:06 se simplifică cu 3 6 împărțit
la 3 este 2 și pe cealaltă diagonală
putem să simplificăm radicalii
simplificăm cu radical din 2 și
obținem 1 în paranteză ne rămâne
1 supra 2 ridicat la puterea a
doua Care este egal cu 1 supra
4 și ultimul exercițiu 6 radical
din 5 la șasea împărțit la radical
din 5 la a opta a fi egal cu radical
din 5 la puterea 6 minus 8 egal
cu radical din 5 la puterea minus
2 egal cu 1 supra radical din 5
la puterea a doua egal cu 1 supra
5