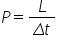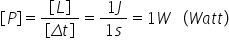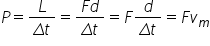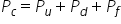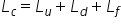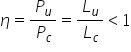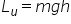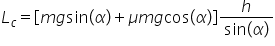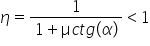Puterea şi randamentul. Exemplul planului înclinat.

în cea de a doua Lecție despre

legile de conservare din mecanică

vom vorbi despre noțiunile de putere

și randament lucru mecanic acoperă

noțiunea de efort depus de un om

sau mașină pentru mișcarea unui

corp dar și nu cea de putere folosit

în aceste mișcare Spre exemplu

Să considerăm că avem o remorcă

de greutate destul de mare să spunem

jumătate de tonă Care este tractată

de un automobil de la București

la Constanța Deci automobilul va

dezvolta o forță de tracțiune f

care va genera această deplasare

dintre București și Constanța lucru

mecanic sau efortul depus pentru

a remorca această remorcă ia același

și pentru o mașină cu o puterea

motorului mai mică să zicem un

Logan dar și pentru o mașină cu

o putere mai mare să zicem un Audi

A6 deci diferența dintre puterea

celor două mașini apare atunci

când Încercăm să facem un acest

lucru această tractare are morții

în tu un timp cât mai scurt atât

timp cât nu consideră intervalul

de timp necesar tractării lucrul

mecanic efectuat este același și

nu putem diferenția între vreau

puterile celor două mașini deci

noțiunea de putere trebuie cumva

legată atât de noțiunile de efort

depus sau în termenii fizicii lucru

mecanic dar și de noțiunea de timp

sau durată necesară depunerii acestui

efort în particular vom sesiza

diferența dintre cele două mașini

cu puteri foarte diferite atunci

când vom cere ca acestei forțe

lucrul mecanic să fie efectuat

un timp cât mai scurt în consecință

puterea se introduce în fizică

prin această Definiți puterea medie

a variația lucrului mecanic efectuat

în unitatea de Timp Aceasta dacă

Considerăm că lucrul mecanic toate

lungul deplasării nu este constant

ceea ce este valabil în general

dacă lucrul mecanic este constant

dar lungul deplasării atunci puterea

efectuată sau puterea dezvoltată

de om sau de mașină va fi lucrul

mecanic împărțită la dacă Forța

de tracțiune forța motoare motoare

este constantă știm că lucrul mecanic

este egal cu produsul dintre forța

constantă și deplasarea produsă

de nici dacă lucru Dacă Forța este

constantă variația lucrului mecanic

va fi f forța constantă înmulțit

cu Delta de și atunci puterea medie

va fi forța înmulțit cu Delta de

împărțit la Delta t Deci puterea

medie va fi produsul dintre forța

constantă și viteza medie de a

lungul deplasări sex cu Tom despre

randament este bine știut că dacă

un om sau mașină depune un efort

sau lucrul mecanic pentru activitate

nu tot efortul sau lucruri depuse

consumă pentru acea activitate

Deci daca avem o anumită putere

sau lucrul mecanic investiti ele

se vor duce în activitatea dorită

sau efectul dorit să spunem efectul

dorit dar întotdeauna vom avea

și efecte nedorite sau colaterale

care nu pot fi evitate Deci o parte

din puterea sau lucrul investit

se va duce și în alte activități

decât cea principală ce a dorit

în general puterea totală sau lucru

total consumat întru activitate

se poate împărți în trei categorii

puterea utilă sau lucru util este

cea investită în efectul pe care

îl dorim în cazul exemplului de

mai devreme al automobilelor care

transportă remorca de la București

la Constanța activitatea dorită

este tractarea remorci la puterea

utilă sau lucru tils film cu puterea

sau lucrul efectuat Exclusiv în

activitatea de tractare a remorci

o altă parte a puterii va fi o

putere disipata sau un lucru de

săpat în învingerea diferitelor

forțe rezistente ce apar Na ce

activitate forțe de frecare de

exemplu între transmisia între

componentele transmisiei automobilului

sau cu șoseaua Dar putem avea și

alte forțe rezistente precum rezistența

aerului la înaintarea mobilului

în special dacă să zicem este o

zi cu o furtună atunci o parte

semnificativă a puterii motorului

generată de motor este consumată

pentru a putea înainta împotriva

unui vânt puternic din față o altă

și a treia categorie de putere

investită este Puterea sau lucru

de funcționare acestea sunt activități

secundare dar necesare Spre exemplu

în cazul automobilului funcționarea

automobilului care duce la efectul

dorit de tractare a remorcii implicăm

și funcționarea multor componente

în implicate direct în tratarea

remorcii putere electrică Un automobil

are nevoie de sisteme electrice

sisteme de direcție care sunt cesare

consumă putere sau lucru mecanic

dar nu sunt implicate direct în

tractare remorci randamentul este

definit ca raportul dintre puterea

utilă și puterea totală consumat

sau în termeni de lucru mecanic

este lucrul mecanic util împărțit

la lucrul mecanic consumat roșii

este o mărime care are foarte multe

sens este raportul dintre cât de

mult efort de punem cât de multă

putere consumam și cât din ea este

folosită pentru activitatea dorită

principală după cum am spus lucrul

mecanic sau puterea consumată totală

va fi suma dintre toate aceste

componente lucrul mecanic util

lucrul mecanic disipat și lucrul

mecanic pentru funcționarea instrumentului

motorului mașinii sau despre ce

este vorba în consecință prin definiție

și prin definiția acestor componente

ale puterii sau lucrul mecanic

total randamentul va fi întotdeauna

mai mic decât tu Haideți să calculăm

randamentul unei mașini simple

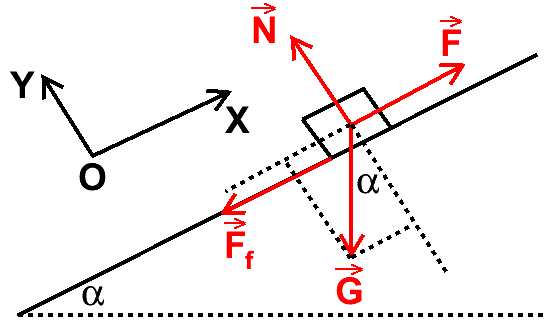
și anume a planului înclinat dinamica

planului înclinat a corpului pe

un plan înclinat a fost rezolvată

într o lecție de mecanică newtonian

planul înclinat o mașină simplă

pentru ridicarea corpurilor grele

la o înălțime H precum arătăm în

această schemă chiar un corp de

masă M și greutate G ridicat un

o anumită înălțime H de o forță

numită forța utilă lucrul mecanic

util este cel folosit strict pentru

această activitate deci el va avea

valoarea lucrul mecanic util este

egal cu forța de care înmulțită

cu deplasarea adică forța de urcare

este egală cu gem greutatea corpului

înmulțită cu h Deci lucrul mecanic

util va fi egal cu m g h un mic

comentariu dacă forța de urcare

este mai mare decât gem atunci

vom obține o accelerație la oricare

care va fi egală cu diferența dintre

cele două forțe împărțite la masă

dar aceasta accelerare a corpului

nu este utilă pentru ridicarea

lui deci de această diferență în

forța de urcare peste greutate

Nu trebuie inclusă în lucru mecanic

util ia finule fac colaterale nefiind

utilă activității principale și

anume de urcare a corpului planul

înclinat face același lucru adică

duce corpul la aceeași înălțime

H dar dea lungul planului înclinat

să calculăm lucrul mecanic total

consumat pentru a face acest lucru

conform schemei 2 deci lucrul mecanic

consumat va fi egală cu forța din

FC din cazul 2 înmulțită cu deplasarea

Care este el pentru a calcula FC

scrie mă forțele pe celor două

coordonate trecem peste câteva

detalii pentru că din nou cazul

dinamicii corpul Pe planul înclinat

a fost rezolvat într o lecție de

mecanică cu de mecanică în italiană

Deci trece direct la ecuațiile

de bază în și obținem că pe axa

o x f c este egal cu forța de frecare

plus mg sinus de Alfa și pe axa

o y în forța normală m este egal

cu mg cosinus de Alfa din nou am

considerat că accelerația corpului

este 0 din același motive ca cele

descrise în cazul 1 rezultă că

f c este egal cu mg pe lângă sinus

de Alfa plus mio cosinus de Alfa

de asemeni știind că l este egal

cu h împărțit la sinus de Alfa

sinus de Alfa este egal cu h împărțit

la el cateta împărțită la ipotenuză

Deci rezultă că lucrul mecanic

consumat este egal cu m g h cu

mulți cu sinus de Alfa plus cosinus

de Alfa împărțit la sinus de Alfa

Deci lucrul mecanic consumat este

egal cu m g h pe lângă 1 plus minus

cotangentă de Alfa că raportul

dintre lucrul mecanic util și lucrul

mecanic consumat obținem randamentul

aceste mașini simple pleci cu împărțit

la el si lucrul mecanic util împărțit

la lucrul mecanic consumat și egal

cu 1 supra 1 plus coeficientul

de frecare cotangentă de Alfa acesta

este randamentul planului înclinat

după cum se observă mai mic decât

unul am ținut cont numai de lucru

mecanic disipat prin frecare cu

planul înclinat la corpului alte

efecte disipative sau consumul

cont colaterale pot fi incluse

în calcularea lucrului mecanic

consumat total și bineînțeles acestea

vor duce la reducerea randamentului

planului înclinat