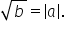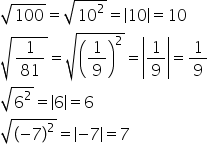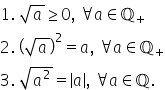Radăcina pătrată
Tag-uri
Partajeaza in Google Classroom
Transcript
rădăcina pătrată a unui număr rațional
pozitiv știind că cinci la puterea
a doua este 25 dar și minus 5 la
puterea a doua este tot 25 Pentru
că atunci când ridicăm un număr
negativ la un exponent par rezultatul
va fi pozitiv zero la puterea a
doua este egal cu 0 minus șapte
la puterea a doua este 49 minus
1 supra 3 la puterea a doua va
fi egal cu 1 supra 9 observăm că
pătratul oricărui număr rațional
este un număr pozitiv sau 0 dacă
avem un pătrat cu aria de 81 m
pătrați Cum putem să calculăm latura
acestuia timp că formula ariei
pătratului este latura la puterea
a doua înseamnă că latura la puterea
a doua va fi egal cu 81 Care este
numărul care ridicat la puterea
a doua de 81 acesta este 9 Deci
latura pătratului va fi 9 m operația
care ne permite să calculăm latura
pătratului atunci când se cunoaște
aria este operația inversă ridicării
la pătrat iar această operație
se numește extragerea rădăcinii
pătrate numărul rațional modul
de a se numește rădăcina pătrată
a numărului b Dacă B este egal
cu a la a doua și scriem rădăcina
pătrată a numărului b sau radical
din b egal cu modul de a să dăm
câteva exemple radical din 5 la
a doua va fi modul de 5 Care este
egal cu 5 radical din minus 5 la
puterea a doua va fi modul de minus
5 Care va fi egal cu 5 radical
din 81 am văzut că este 9:00 pentru
că 9 la a doua este 81 radical
din 16 va fi 4 pentru că 4 x 4
este 16 radical din 100 este 10
radical din minus 16 este o operație
care nu are sens deoarece nici
un număr rațional ridicat la puterea
a doua nu va fi negativ Deci nu
că serviciul număr are ridicat
la pătrat să fie minus 16 mo spune
că această operație Nu are sens
să ne reamintim Ce înțelegem prin
tu un pătrat perfect Un număr natural
se numește pătrat perfect dacă
este pătratul unui număr întreg
pentru a calcula rădăcina pătrată
dintre număr natural pătrat perfect
om Descompune numărul în produs
de pătrate perfecte de exemplu
de propuneri să calculăm rădăcina
pătrată a numărului 1.600 1600
se poate scrie 16 ori 116 și 100
sunt pătrate perfecte 16 înseamnă
4 la puterea a doua iar 100 este
10 la puterea a doua egal mai departe
Putem să scriem 4 ori 10 totul
la puterea a doua egal cu 40 la
puterea a doua și atunci radical
din 1600 va fi 40 pentru că 40
la a doua este 1600 să vedem cât
va fi radical din 256 Să descompunem
acest număr un produs de pătrate
perfecte 256 Se împarte exact la
doi doi în doi intra odată doi
în cinci de două ori 216 de 8 ori
128 se împarte la 2 și obținem
64 deoarece aici avem deja un pătrat
perfect nu mai continuăm descompunerea
a pentru că scopul nostru nu este
Să descompunem numărul în factori
primi și în produs de pătrate perfecte
64 se împarte la 64 și atunci numărul
256 Se va scrie 2 la puterea a
doua ori 64 Care este egal cu 2
la a doua ia 64 este pătratul numărului
8 2 la a doua ori 8 la a doua ceva
scrie 2 ori 8 totul la puterea
a doua care va fi egal cu 16 la
puterea a doua Deci cantica din
256 este 16 pentru că 16 la a doua
este 256
Rădăcina pătrată a unui număr rațional pozitivAscunde teorie X
Navigare în lectii
Cumpara abonament
