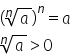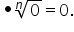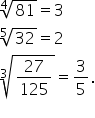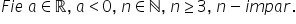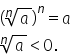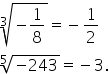Radicali de ordin n
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție vom discuta despre
radicali de ordin superior Fie
a un număr real nenegativ atunci
prin rădăcina pătrată se înțelege
un număr real X care ridicat la
pătrat de o valoare egală cu a
rădăcina pătrată se mai numește
și radical de ordin doi din moment
ce orice număr ridicat la pătrat
este pozitiv înseamnă că rădăcina
pătrată se poate extrage doar din
numere pozitive pentru că extragerea
rădăcinii pătrate și ridicarea
la putere sunt operații inverse
de asemenea radical din a este
întotdeauna mai mare sau egal cu
0 în mod asemănător vom defini
și rădăcina cubică sau rădăcina
de ordinul 3 dacă a este un număr
real se pune problema existenței
unui număr real x astfel încât
x la a treia să fie egal cu a de
exemplu ne punem întrebarea Care
este latura unui cub având volumul
egal cu 8 știind că 2 la a treia
este egal cu opt prin urmare latura
cubului va fi egală cu 2 boxe pune
astfel că radical de ordin 3 din
8 este egal cu 2 sau radical indice
3 din 8 egal cu 2 să vedem alte
câteva exemple 3 la a treia este
27 prin urmare radical de ordin
3 din 27 va fi egal cu 3 minus
2 la a treia este egal cu minus
8 Așadar radical indice 3 din minus
8 va fi egal cu minus 2 observăm
că în cazul radicalului de ordin
3 din a nu mai trebuie să punem
condiția ca ei să fie număr nenegativ
Așadar Fie a un număr real atunci
radical de ordin 3 din a este acel
număr x cu proprietatea că x la
a treia este egal cu A dacă A este
pozitiv atunci și x este pozitiv
iar dacă a este negativ atunci
și x este negativ în continuare
vom extinde noțiunea de radicali
și vom aborda două cazuri mai întâi
vom discuta despre radical de ordin
n din număr real pozitiv dacă a
este un număr real pozitiv iar
n un număr natural mai mare sau
egal cu 2 atunci numărul reale
notate astfel se numește radical
de ordin n din a și este numărul
real pozitiv cu proprietatea că
radical de ordin n din a la puterea
n este egal cu a mai putem citind
radical indice n din a în cazul
particular în care a este 0 atunci
radical de ordin n din zero va
fi egal cu zero să vedem câteva
exemple radical de ordin 5 din
32 este egal cu 2 pentru că 2 la
cincea este egal cu 32 sau radical
indice 4 din 81 va fi egal cu 3
pentru că 3 la a patra este 81
radical de ordin 3 din 27 supra
125 va fi egal cu 3 supra 5 pentru
că 3 supra 5 la treia este egal
cu 27 supra 125 în continuare vom
discuta despre radical de ordin
impar dintre un număr negativ Fie
a un număr real negativ n un număr
natural n mai mare sau egal decât
3n impar am văzut mai devreme când
am discutat despre radicalul de
ordin trei că atunci când era negativ
și radical de ordin 3 din a era
negativ în general dacă a este
număr negativ atunci putem extrage
doar radical de ordin impar Așadar
dacă a este număr negativ atunci
radical de ordin n din a este numărul
negativ cu proprietatea că radical
de ordin n din a la puterea n este
egal cu a să vedem câteva exemple
radical de ordin 3 din minus 1
pe 8 va fi egal cu minus 1 pe 2
sau radical de ordin 5 din minus
243 este egal cu minus 3 pentru
că minus 3 la puterea a 5-a este
egal cu minus 243 în concluzie
să reținem că atunci când avem
numere reale pozitive putem extrage
radicalul de ordin par și impar
dar atunci când avem numere negative
se poate extrage doar radical de
ordin impar

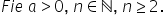
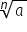 cu proprietățile:
cu proprietățile: