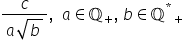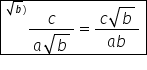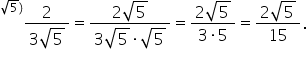Raţionalizarea numitorului unei fractii

semnalizarea numitorului unei fracții

raționalizarea este procedeul prin

care transformăm un număr irațional

dintr un număr rațional dacă avem

de exemplu fracția 1 supra radical

din 5 observăm că numitorul este

un număr irațional pentru al transforma

un număr rațional Trebuie să găsim

un alt număr care înmulțit cu el

ma transforma produsul într un

număr rațional pentru aceasta a

folosit proprietățile radicalilor

învățate până acum știind că radical

din 5 ori radical din 5 este egal

cu radical din 5 ori 5 egal mai

departe cu radical din 25 Care

este egal cu 5 observăm așa dacă

dacă înmulțim la decal din 5 cu

el însuși produsul astfel obținut

este 5 Care este un număr rațional

și atunci pentru a transforma numitorul

aceste fracții în pronume rațional

va trebui să amplificăm fracția

cu radical din 5 prin amplificare

obținem următoarea fracție cu 1

ori radical din 5 este radical

din 5 iar la numitor avem radical

din 5 ori radical din 5 egal mai

departe cu radical din 5 supra

radical din 25 egal cu radical

din 5 supra 5 în general dacă numitorul

unei fracții este un număr irațional

de forma radical din b sau a radical

din b prin amplificarea fracției

cu numărul radical din b numitorul

de vine un număr rațional îmi spune

că avea acțional is ați numitorul

în continuare vom da câteva exemple

primul exemplu 2 supra radical

din 3 ne propunem să raționalizând

numitorul aceste fracții amplifica

fracția cu radical din 3 și obținem

la numărător 2 ori radical din

3 care se scrie 2 radical din 3

supra radical din 3 ori radical

din 3 egal în continuare cu 2 radical

din 3 supra radical din 9 egal

mai departe cu 2 radical din 3

supra 3 al doilea exemplu 10 radical

din 5 supra radical din 2 numitorul

este numărul irațional radical

din 2 iar pentru a raționaliza

numitorul amplificăm fracția cu

radical din 2 și obținem 10 radical

din 5 ori radical din 2 supra radical

din 2 ori radical din 2 egal continuare

cu 10 radical din 10 radical din

2 ori radical din 2 este radical

din 4 adică 2 această fracție se

mai poate simplifica cu 2 deoarece

10 este un multiplu al lui 2 simplificând

cu 2 obținem la numărător 5 iar

la numitor 1 Așadar rezultatul

va fi 5 radical din 10 al treilea

exemplu 2 radical din 2 supra radical

din 5 amplificând fracția cu radical

din 5 și obținem 2 radical din

2 ori radical din 5 supra radical

din 5 ori radical din 5 egal mai

departe cu 2 radical din 10 supra

5 4 7 supra 3 radical din 11 la

numitor avem produsul dintre numărul

rațional 3 și numărul irațional

radical din 11 pentru a raționaliza

numărul radical din 11 amplificând

fracția cu radical din 11 vom obține

7 radical din 11 supra 3 radical

din 11 ori radical din 11 egal

mai departe cu 7 radical din 11

supra 3 ori radical din 11 orade

cal din 11 este 11 egal mai departe

cu 7 radical din 11 supra 33 5

minus 4 supra 5 radical din 3 numărul

irațional de la numitor este radical

din 3 Așadar trebuie să amplificăm

fracția cu radical din 3 și vom

obține minus 4 radical din 3 supra

5 radical din 3 ori radical din

3 egal mai departe cu minus 4 radical

din 3 supra 5 ori 3 egal cu minus

4 radical din 3 supra 15 6 durerea

de cal din 13 supra 7 radical din

2 numărul irațional de la numitor

este radical din 2 amplificăm fracția

cu acesta vom obține la numărător

2 radical din 13 ori radical din

2 supra 7 radical din 2 ori radical

din 2 egal cu 2 radical din 26

supra 7 ori 2 putem să simplificăm

cu 2 și obținem rezultatul radical

din 26 supra 7 următorul exercițiu

numărul 7 1 minus radical din 2

supra radical din 5 amplificând

fracția cu radical din 5 atenție

numărul radical din cinci trebuie

înmulțit cu toată expresia de la

numărător și atunci casei factum

corect va trebui să punem o paranteză

Deci avem radical din 5 pe lângă

1 minus radical din 2 supra radical

din 5 ori radical din 5 pentru

a desface această paranteză vom

folosi distributivitatea înmulțirii

față de scădere și vom înmulțim

numărul radical din cinci cu fiecare

număr din paranteză mă mai ține

radical din 5 ori 1 care este radical

din 5 minus radical din 5 ori radical

din 2 iar la numitor radical din

5 ori radical din 5 este 5 egal

mai departe cu radical din 5 minus

radical din 10 supra 5 8 radical

din 2 minus radical din 7 supra

3 radical din 3 numărul irațional

de la numitor este radical din

3 Așadar Baum amplificat fracția

cu radical din 3 numărul radical

din 3 se înmulțește cu toate expresia

de la numărător și vom scrie radical

din 3 pe lângă radical din 2 minus

radical din 7 supra 3 radical din

3 ori radical din 3 egal mai departe

radical din 3 ori radical din 2

minus radical din 3 ori radical

din 7 supra 3 ori 3 pentru că radical

din 3 ori radical din 3 este 3

aici înmulțim acești radical radical

din 3 ori radical din 2 este radical

din 6 minus radical din 3 ori radical

din 7 este radical din 21 iar la

numitor avem trei ori trei adică

nouă următorul exercițiu 6 radical

din 3 supra radical din 32 mai

întâi vom scoate factorii de sub

acest radical a trebuit Să descompunem

în factori primi numărul 32 32

este un număr par Deci se împarte

la doi și obține rezultatul 16

16 împărțit la 2 este opt opt părți

la 2 este 440 la 2 este 2 și 2

împărțit la 2 este 1 grupa în factorii

câte doi alăturat trece efectul

care se repetă și obținem ca radical

din 32 este egal cu 2 ori 2 adică

4 radical din 2 numărul care a

rămas fără pereche este trece sub

radical Și atunci vom scrie 6 radical

din 3 supra 4 radical din 2 numărul

irațional de la numitor este radical

din 2 Și atunci vom Amplifică fracția

cu radical din 2 obținem astfel

6 radical din 3 ori radical din

2 supra 4 radical din 2 ori radical

din 2 egal cu 6 radical din 6 supra

4 ori 2 putem să simplificăm cu

2 6 împărțit la 2 este 3 2 împărțit

la 2 este 1 și obținem 3 radical

din 6 supra 4 și ultimul exercițiu

10 număr adică el din 2 supra radical

din 45 descompunem numărul 45 în

factori primi 45 se împarte la

3 Fiindcă suma cifrelor sale este

9 45 împărțit la 3 este 15 15 se

împarte la trei și obținem 5 5

împărțit la 5 este 1 Groupama câte

doi și observați de radical din

45 va fi egal cu 3 radical din

5 Și atunci vom scrie egal cu 9

radical din 2 supra 3 radical din

5 amplificând fracția cu radical

din 5 ce obținem 9 radical din

2 ori radical din 5 supra 3 radical

din 5 ori radical din 5 egal voi

continua aici egal cu 9 radical

din 10 supra 3 ori 5 simplificăm

9 și 3 9 împărțit la 3 este 3 și

3 împărțit la 3 este 1 și obținem

rezultatul final 3 radical din

10 supra 5