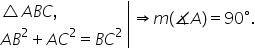Reciproca teoremei lui Pitagora

în această lecție o să învățăm

reciproca teoremei lui Pitagora

această teoremă este foarte utilă

atunci când dorim să demonstrăm

că un triunghi este dreptunghic

dacă un triunghi pătratul lungimii

unei laturi este egal cu suma pătratelor

lungimilor celorlalte două laturi

atunci triunghiul este dreptunghic

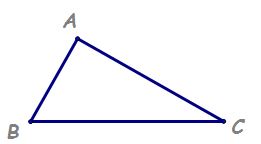
demonstrație teoremă presupunem

că avem un triunghi oarecare abc

în care avem următoarea relație

bc la pătrat egal cu AB la pătrat

plus AC la pătrat trebuie să arătăm

în concluzie că măsura unghiului

a este egală cu 90 de grade pentru

aceasta am construit un triunghi

mnp astfel încât măsura unghiului

m să fie egală cu 90 de grade m

and să fie congruent cu AB și mp

congruent cu ac pentru a demonstra

că triunghiul ABC este dreptunghic

m demonstrați că triunghiul ABC

este congruent cu triunghiul MNP

triunghiul MNP având unghiul m

cu măsura de 90 de grade va rezultat

din congruența celor două triunghiuri

ca și măsura unghiului a va fi

de 90 de grade Așadar Să arătăm

că triunghiul ABC este congruent

cu triunghiul MNP dacă triunghiul

MNP este dreptunghic atunci putem

să aplicăm teorema lui Pitagora

în acest triunghi aplicăm teorema

lui Pitagora În triunghiul MNP

ma rezultată mp la pătrat este

egal cu m n la pătrat plus mp la

pătrat Dar m n este congruent cu

AB deci putem să scriem egal cu

AB la pătrat plus AC la pătrat

dar a b la pătrat plus AC la pătrat

este egal cu bc la pătrat din ipoteză

am arătat astfel că m pe la pătrat

este egal cu bc la pătrat atunci

va rezulta că NP este egal cu bc

sau altfel scris n p este congruent

cu BC am arătat astfel că cele

două triunghiuri au toate cele

trei laturi respectiv congruente

m n este congruent cu AB din construcția

făcută m p este congruent cu ac

și am demonstrat că NP este congruent

cu b c din relațiile 1 2 și 3 rezultă

că triunghiul MNP este congruent

cu triunghiul abc din această relație

de congruență rezultă că unghiul

m este congruent cu unghiul a dar

măsura unghiului m este egală cu

90 de grade din construcție și

atunci va rezulta că măsura unghiului

a va fi și aceasta egală cu 90

de grade este la mare tot că triunghiul

ABC este un triunghi dreptunghic

în A rețineți că dacă întru un

triunghi se verifică această relație

a la a doua plus b la a doua egal

cu c la a doua unde a b și c sunt

lungimile laturilor triunghiului

atunci triunghiul este dreptunghic

o să facem în continuare o problemă

dacă triunghiul abc are laturile

AB AC și BC direct proporționale

cu numerele 5 12 și 13 iar perimetrul

triunghiului este egal cu 60 cm

Arătați că triunghiul este dreptunghic

dacă laturile triunghiului sunt

direct proporționale cu 5 12 și

13 atunci Putem să scriem următoarea

relație a b supra 5 este egal cu

a c supra 12 și egal cu bc supra

13 putem egala aceste rapoarte

în continuare cu raportul dintre

suma numărătorilor și suma numitorilor

egal cu ab plus AC plus BC supra

5 plus 12 plus 13 egal Se știe

că perimetrul triunghiului este

60 cm iar suma pe care am obținut

o noi la numărător este tocmai

perimetrul triunghiului Putem să

scriem egal mai departe cu perimetrul

triunghiului ABC supra 5 plus 12

este 17 plus 13 egal cu 30 perimetrul

triunghiului este 60 Ia 60 supra

30 este egal cu 2 pentru a afla

lungimile laturilor triunghiului

egală în fiecare raport cu 2ab

supra 5 este egal cu 2 de aici

va rezulta că ab este egal cu 285

și egal cu 10 cm ace supra 12 este

egal cu 2 rezultă ac egal cu 12

ori 2 egal cu 24 cm și BC supra

13 este egal cu 2 de aici ma rezultă

că bc este egal cu 13 ori 2 egal

cu 26 cm pentru a verifica dacă

triunghiul abc este dreptunghic

folosind reciproca teoremei lui

Pitagora observăm că cea mai mare

latură a triunghiului este latura

b c înseamnă că latura bc ar trebui

să fie ipotenuză în cazul în care

triunghiul ar fi dreptunghic iar

laturile ab și ac sunt catete folosind

reciproca teoremei lui Pitagora

și arătăm că ab la pătrat plus

AC la pătrat va fi egal cu bc la

pătrat verificăm această relație

a de la a doua plus AC la a doua

egal cu bc la a doua AB este egal

cu 10 10 la pătrat plus 24 la pătrat

egal cu 26 la pătrat 10 la a doua

este egal cu 124 la a doua este

576 Puteți să faceți și voi calculul

iar 26 la a doua este 676 100 plus

576 este egal cu 676 am obținut

astfel o relație adevărată și atunci

folosind reciproca teoremei lui

Pitagora va rezulta că triunghiul

ABC este un triunghi dreptunghic

având măsura unghiului a egală

cu 90 de grade am arătat astfel

că această relație este verificată