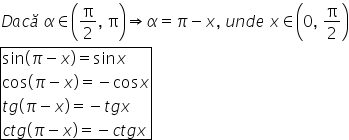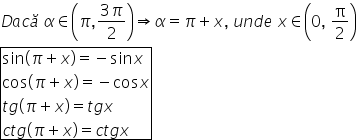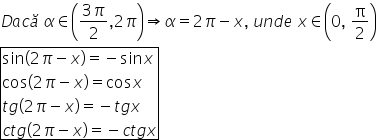Reducerea la primul cadran

atunci când trebuie să calculăm

valorile funcțiilor trigonometrice

ale unghiurilor din cadranele 2

3 și 4 pentru a ușura calculele

vom scrie aceste unghiuri cu ajutorul

unghiurilor din cadranul întâi

la fel vom proceda și atunci când

trebuie să calculăm funcții trigonometrice

pentru unghiul cu măsura mai mare

de 360 de grade Deci care depășesc

primul cerc bunele proprietăți

ale funcțiilor trigonometrice care

se pot observa Pe cercul trigonometric

și mama reduce calculul acestora

la primul cadran mai întâi să vedem

cum se face trecerea din cadranul

al doilea în cadranul întâi avem

unghiul a o m situat în primul

cadran pe care îl am notat cu x

și unghiul a o m prim situat în

cadranul al doilea pe care dorim

să le exprimăm cu ajutorul unghiului

x punctele m și m prim sunt simetrice

prin urmare unghiul a o m are aceeași

măsură cu unghiul a prim o m prim

din moment ce unghiul a o a prim

are măsura egală cu 180 de grade

sau pere adiel atunci unghiul a

o m prim va fi egal cu pi minus

x prin urmare dacă unghiul Alfa

este un unghi situat în cadranul

al doilea De cine intervalul pi

supra 2 pi atunci acestui unghi

se va scrie pe minus x unde x este

un om situat în primul cadran și

acum să exprimăm sinusul acestui

unghi sinusul unghiului aom prim

Este dat de proiecția punctului

m prim pe axa o y iar aceasta este

punctul B dar și proiecția punctului

m pe axa o y este tot punctul b

prin urmare ordonantele acestor

puncte coincide Putem să scriem

așa dar că sinusul unghiului P

minus x este egal cu sinus de x

cosinusul unghiului pi minus x

este abscisa punctului m prim dar

aceasta este negativă întrucât

punctul a prim este situat la stânga

axa o y și atunci cosinusul unghiului

pe minus x va fi egal cu minus

cosinus de x cele două segmente

o a și o a prim sunt egale în modul

însă accizele acestor două puncte

au semne diferite să vedem în continuare

tangenta și cotangenta tangenta

unghiului x este dată de ordonata

punctului m de pe tangentă deci

vorbim de segmentul a m iar tangenta

unghiului b minus x este dată de

ordonata punctului m prim cele

două segmente a m și a m prim au

aceeași lungime însă punctul M

prim este situat sub axa o x Așadar

ordonata punctului m prim va fi

negativă Deci tangentă de penis

x este egal cu minus tangentă de

x cotangentă unghiului x este dată

de abscisa punctului s deci vorbim

de segmentul b s iar cotangenta

unghiului b minus x este dată de

lungimea segmentului s prim b însă

punctul a prim este situat la stânga

axa o y Așadar abscisa acestui

punct este negativă Deci cotangentă

de pe minus x este egal cu minus

cotangentă de x să vedem în continuare

Cum se face trecerea din cadranul

al treilea în cadranul întâi avem

cu unghiul aom pe care îl am notat

cu x și unghiul a o m prim situat

în cadranul al treilea pe care

dorim să le exprimăm cu ajutorul

unghiului x unghiurile a o m și

a prim o m prim au aceeași măsură

pentru că sunt unghiuri opuse la

vârf iar măsura unghiului a o a

prim este egală cu 180 de grade

sau pira Deian atunci unghiul a

o m prim din cadranul al treilea

se poate scrie plus x unde x este

unghiul din cadranul 1 Alfa este

un om din cadranul al treilea din

intervalul pi 3 pi supra 2 Iar

acest unghi se va scrie pic plus

x unde x este un unghi din primul

cadran proiecția punctului m prim

pe axa o y este punctul B prim

iar proiecția punctului m pe axa

o y este punctul b prin urmare

ordonata punctului m prin va fi

negativă întrucât acest punct este

situat sub axa o x și atunci sinusul

unghiului pai plus x plus y egal

cu minus sinus de x cosinus acestui

unghi este dat de abscisa punctului

m prim observăm că punctul a prim

este situat la stânga axa o y a

prin urmare cosinusul unghiului

A plus x este egal cu minus cosinus

de x iar cosinus de x este abscisa

punctului m adică proiecția lui

m pe axa o x să vedem în continuare

tange și cotangenta tangenta unghiului

x este reprezentată de ordonata

punctului m deci vorbim de lungimea

segmentului a m iar tangenta unghiului

pai plus x dacă prelungim această

raza vectoare obținem același punct

m pe tangentă prin urmare tangenta

unghiului pi plus x este egală

cu tangenta unghiului x cotangenta

unghiului x este dată de lungimea

segmentului b s iar cotangenta

unghiului pai plus x este de asemenea

egală cu bs prin urmare cotangentă

de pe plus x este egal cu cotangentă

de x și la final să vedem trecerea

din cadranul 4-lea în cadranul

întâi avem unghiul a o m din cadranul

întîi pe care îl am notat cu x

și dorim să exprimăm unghiul a

o m prim acesta în funcție de x

știind că un cerc întreg are doi

pira Deian sau 360 de grade prin

urmare unghiul a o m prim din cadranul

al patrulea va fi egal cu 2 minus

x unde x este unghiul din cadranul

1 dacă Alfa este unghiul din cadranul

al patrulea adică din intervalul

3 pi supra 2 2 pi atunci Alfa se

va scrie 2 pi minus x unde x este

unghiul din cadranul întâi acum

sinusul acestui unghi este dat

de proiecția punctului m prin pe

axa o y Deci avem punctul B prim

iar sinusul unghiului x este dat

de proiecția punctului m pe axa

o y Deci punctul B observăm Așadar

că ordonata punctului m prim Este

negativă prin urmare sinusul unghiului

2 pi minus x va fi egal cu minus

sinus de x cosinus de 2 pi minus

x este egal cu cosinus de x deoarece

abscisele acestor puncte m și m

prim coincid proiecția lui m pe

axa o x este punctul A iar proiecția

lui m prim pe axa o x este de asemenea

punctul a și să vedem tangenta

și cotangenta tangenta unghiului

x este dată de ordonata punctului

m Deci vorba de lungimea segmentului

a m iar tangenta unghiului 2 primim

fix este dată de ordonata punctului

m prim din moment ce punctul M

prim este situat sub axei o x atunci

putem scrie că tangentă de 2 pi

minus x va fi egal cu minus tangentă

de x cotangenta unghiului x este

dată de abscisa punctului iar cotangenta

unghiului 2 pi minus x este dată

de abscisa punctului exprim Deci

cotangentă de 2pi minus x va fi

egal cu minus cotangentă de x în

clipul urmator o să vedem cum putem

să aplicăm aceste relații pentru

a calcula valorile unor funcții

trigonometrice