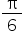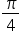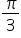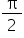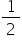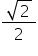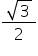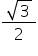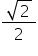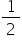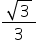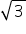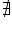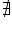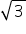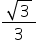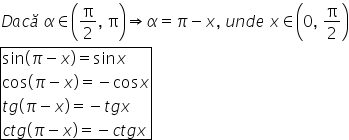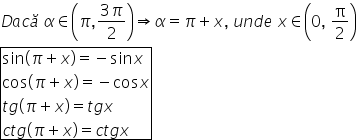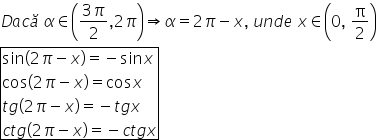Reducerea la primul cadran (aplicații)

în acest clip o să calculăm valorile

unor funcții trigonometrice folosind

aceste relații de trecere la primul

cadran și periodicitatea funcțiilor

trigonometrice reamintesc că funcțiile

sinus și cosinus sunt periodice

având perioada principală 2 pi

de sinus de x plus doi capii este

egal cu sinus de x și cosinus de

x plus 2k este egal cu cosinus

de x aceste relații sunt valabile

pentru orice numar real X funcțiile

tangentă și cotangentă sunt periodice

având perioada principală pai Deci

tangentă de x plus copy este egal

cu tangentă de x această relație

este valabilă pentru orice numar

real x diferit de multipli impari

de pi supra 2 iar funcția cotangentă

are De asemenea perioada principală

pai Deci cotangentă de x plus k

este egal cu cotangentă de x această

relație este valabilă pentru orice

numar real x diferit de multipli

întregi de pini și acum Haideți

să calculăm cosinus de 300 de g

ne propunem să scriem această valoare

cu ajutorul unui unghi din cadranul

întâi deoarece cunoaștem deja sau

ar trebui să știm valorile funcțiilor

trigonometrice pentru unghiurile

uzuale de 30 45 și 60 de grade

și atunci 300 de g se poate scrie

360 de grade minus 60 de grade

dar 360 este 2 pi și atunci aplicăm

această formulăm cosinus de 2 pi

minus x este egal cu cosinus de

x Deci avem egale cu cosinus de

60 de grade și egal cu 1 pe 2 să

calculăm acum sinus de 225 de grade

225 se poate scrie 180 plus 45

180 este pi și atunci aplicăm formula

sinus de pi plus x iatom sinus

de pi plus x este egal cu minus

sinus de x Deci avem minus sinus

de 45 de grade și a egal cu minus

radical din 2 pe 2 vom calcula

acum tangentă de 405 grade 405

se poate scrie 360 Plus 45 360

înseamnă 2 pi radiani putem să

aplicăm periodicitatea funcției

tangentă tangentă de x plus capii

este egal cu tangentă de x prin

urmare o să avem aici tangentă

de 45 de grade și egal cu 1 să

calculăm în continuare sinus de

240 de grade 240 se poate scrie

180 plus 60 180 înseamnă pi radiani

și atunci aplicăm formula sinus

de pi plus x este minus sinus de

x Deci o să avem minus sinus de

60 de grade și egal cu minus radical

din 3 pe 2 să cosinus de 7 pi supra

6 7 pi supra 6 se poate scrie P

PLUS pi pe 6 aplicăm această formulă

și obținem minus cosinus de pi

supra 6 și egal cu minus radical

din 3 pe 2 tangentă de 11 pi supra

6 11 supra 6 se poate scrie 12

pi supra 6 minus pi supra 6 inel

cu tangentă de 2 pi minus y supra

6 tangentă de 2 pi minus x este

egal cu minus tangentă de x Deci

avem minus tangentă de pi supra

6 egal cu minus radical din 3 pe

3 să calculăm acum cotangentă de

7 pi supra 4 7 pe 4 se poate scrie

8 pi pe 4 minus pi supra 4 egal

cu cotangentă de 2pi minus pi supra

4 cotangentă de 2pi minus x este

minus cotangentă de x egal cu minus

cotangentă lipit pe 4 și egal cu

minus unu cosinus de 85 pi supra

6 efectuăm această împărțire obținem

14 rest 1 Deci avem 14 pi plus

p supra 6 egal 14 pi este multiplu

de 2 pi folosind periodicitatea

funcției cosinus și avem egal cu

cosinus de pi supra 6 Care este

radical din 3 pe 2 și unul din

exercițiu cotangentă de 373 pi

supra 3 efectuăm și aici împărțirea

avem 124 plus pi supra 3 cotangentă

de x plus copy este egal cu cotangentă

de x egal cu cotangentă de pi supra

3 și egal cu radical din 3 pe 3