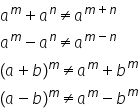Reguli de calcul cu puteri. Observații
Tag-uri
Partajeaza in Google Classroom
Transcript
Haideți să facem acum trei observații
legate de regulile de calcul cu
puteri pentru că e posibil să aplicăm
aceste reguli chiar și când mai
e cazul prima observație știind
că atunci când avem de exemplu
2 la a treia înmulțit cu 2 la a
doua având un produs de puteri
cu aceeași bază copiem bază și
adunăm exponenții Deci avem trei
plus doi Deci avem doi la a cincea
adică 32 bun însă dacă între cele
două puteri nu avem operația de
înmulțire ce avem operația de adunare
adică 2 la a treia a adunat cu
2 la a doua ce obținem Atunci eu
are egal tot cu 2 la 3 plus 2 e
bine Nu în situația în care între
puteri avem adunare sau scădere
nu contează dacă puterile au aceeași
bază sau același exponent noi vom
ridica ca maine vom face mai întâi
ridicările la putere decentei calculăm
Cât e 2 la a treia apoi Cât este
2 la a doua iar apoi facem suma
de 2 la a treia înseamnă doi ori
doi ori doi adică 8 adunat cu 2
la a doua înseamnă doi ori doi
Deci patru cu alte cuvinte obținem
aici 12 Păi e clar din ce am notat
aici că 2 la a treia adunat cu
2 la a doua nu este același lucru
cu 2 la 3 plus 2 deci nu vom însumat
exponenții aici obținem 12 iată
în timp ce 2 la 3 plus 2 adică
2 la a cincea ne dă 32 cea de a
doua observație Doina 6-a împărțit
la 2 la a doua ce avem pe având
o împărțire de puteri cu aceeași
bază copiem paza și scădem exponenții
adică 6 minus doi Deci ne dă 2
la a patra care înseamnă 16 dacă
avem însă 2 la a șasea minus acum
2 la a doua obținem 2 la 6 minus
doi deja am spus că atunci când
între puteri avem adunare sau scădere
face mai întâi ridicările la putere
Deci calculăm Cât e 2 la a șasea
Cât este 2 la a doua și apoi facem
diferența 2 la a șasea Haideți
să notăm aici 2 la a șasea înseamnă
doi ori doi Deci trebuie să avem
șase factori toți egal cu doi avem
aici 8 înmulțit cu 8 Deci ne dă
64 da cu el cuvinte aven 64 minus
2 la a doua ne dă patru deci Rezultatul
este 60 Haideți să ștergem aici
Bun cu alte cuvinte Ce rezultă
de aici că 2 la a șasea minus 2
la a doua nu este egal cu 2 la
6 minus 2 deja că în cazul înmulțirii
respectivul împărțirii facem suma
Iată sau diferența exponenților
când între puteri dacă avem adunare
sau scădere atunci face mai întâi
ridicările la putere nu contează
dacă avem aceeași bază sau poate
același exponent Tot așa se întâmplă
și în această situație De ce a
treia observație Iată 3 înmulțit
cu 4 ridicat la a doua nu știm
că în acest caz e exponentul 2
merge la fiecare număr în adică
avem trei la a patra ori pardon
3 la a doua aici avem trei la a
doua înmulțit cu 4 la a doua bun
Dacă însă avem operație de adunare
aici adică 3 plus 4 la a doua o
vioară egal cu 3 la a doua este
cel semnul întrebării o fi War
egal cu 3 la a doua adunat cu 4
la a doua Păi Haideți să facem
calculul 3 plus 4 ne dă 7 la a
doua adică ne dă 49 ce avem aici
3 la a doua care seamănă 9 4 la
a doua înseamnă 16 adică 9 plus
16 care ne dă 25 pe Clara avem
numere diferite Da deci Haideți
să ștergem acest semn de întrebare
și vom trece diferit Iată am găsit
și această observație care ne spune
că în acest caz mai întâi trebuie
să facem calculul din paranteză
și apoi ridicăm la puterea a doua
Deci nu vom aplica regula învățată
aici absolut la fel se întâmplă
și dacă avem diferență de exemplu
4 minus 3 ca să facem diferența
nu am trecut trei minus patru la
a doua este egal cu 4 la a doua
minus 3 la a doua Păi 4 minus 3
ne dă 1 la a doua adică 1 4 la
a doua ne dă 16 3 la a doua ne
dă nouă de facem diferența ne dă
7 pe Clara avem diferit Deci venim
și ștergem aici asta înseamnă că
4 minus 3 totul la a doua nu e
același lucru cu patru la a doua
minus 3 la a doua cu alte cuvinte
să reținem că această regulă Da
se aplică doar dacă între numerele
din paranteză avem operație de
înmulțire sau împărțire Deci să
reținem aceste observații pentru
a aplica regulile atunci când este
cazul
Observații la reguli de calcul cu puteriAscunde teorie X
Navigare în lectii
Cumpara abonament
