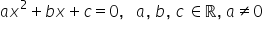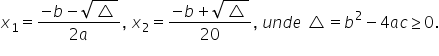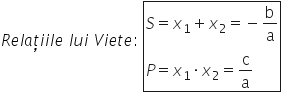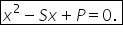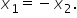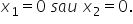Relațiile lui Viete

în această lecție o să discutăm

despre Relațiile lui viet și despre

natura și semnul rădăcinilor ecuației

de gradul al doilea transfer vit

a fost în matematicieni francez

care a avut contribuții importante

în algebră elan găsit o legătură

între soluțiile ecuației de gradul

al doilea și coeficienții acesteia

Maria amintească Forma generală

a unei ecuații de gradul al doilea

este ax pătrat plus bx plus c egal

cu 0 unde a b și c sunt numere

reale cu a diferit de 0 sa notat

cu Delta discriminantul ecuației

acesta este b pătrat minus patru

ace în cazul în care Delta este

pozitiv ecuația admite două ore

de cereale și anume X1 egal cu

minus b minus radical din Delta

supra 2-a și X2 egal cu minus b

plus radical din Delta supra 2-a

în continuare o să deducem Relațiile

lui viet Acestea se referă la suma

și produsul celor două rădăcini

ale ecuației de gradul al doilea

Așadar vom calcula mai întâi rădăcini

lor X1 plus X2 și avem minus b

minus radical din Delta supra 2-a

plus minus b plus radical din deltă

supra 2-a pentru că fracțiile au

același numitor vom aduna numărătorii

și avem minus 2 minus radical din

Delta minus b plus radical din

deltă supra 2-a se reduce minus

radical din Delta cu plus radical

din Delta și obținem minus 2 b

supra 2-a se simplifică doi cu

doi și în final obținem minus b

supra a să ne ținem Așadar această

formulă x 1 plus x 2 este egal

cu minus b supra a aceasta este

prima relație a lui viet iar pentru

a găsi a doua relația lui ithome

exprimat produsul rădăcinilor X1

X2 și avem minus b minus radical

din Delta supra 2-a totul pe lângă

minus b plus radical din Delta

supra 2-a egal la numărător aplicăm

o formulă de calcul prescurtat

a minus b pe lângă a plus b este

egal cu a la a doua minus b la

a doua Așadar la numără vom avea

a minus b la pătrat minus radical

din Deltă la pătrat totul supra

4-a la a doua egal cu b la a doua

minus Delta supra 4-a la pătrat

însă b la a doua minus Delta este

egal cu patru ace Iată dacă ne

uităm la această relație avem b

pătrat minus 4 ac egal cu Delta

prin urmare de pătrat minus Delta

este egal cu 4-a si Așadar la numărător

mă îmi scrie patru ace supra 4-a

pătrat se simplifică 4 cu 4 și

a și obținem în final ce supra

a așa dar cea de a doua relație

a lui viet X1 X2 egal cu c supra

a aceste formule ne permit să calculăm

suma și produsul rădăcinilor ecuației

de gradul al doilea fără să cunoaștem

rădăcinile Așadar este important

să reținem cele două relații ale

lui viette ia tele x 1 plus x 2

este egal cu minus b supra a și

x 1 x 2 egal cu c supra a să vedem

un exemplu concret avem următoarea

ecuație de gradul al doilea 4 x

pătrat minus 3x minus 1 egal cu

0 Haideți să scriem Relațiile lui

viet pentru această ecuație mai

întâi este foarte important să

cunoaștem coeficienții acesteia

a este coeficientul lui x la a

doua adică 4 b este coeficientul

lui x adică minus 3 iar c este

termenul liber minus unu Așadar

prima relație a lui viette X1 plus

X2 va fi egal cu minus b supra

a minus minus 3 supra 4 egal cu

3 pe 4 iar x 1 x 2 este egal cu

c supra a egal cu minus 1 supra

4 aceste formule sunt importante

Deoarece ele ne permit să formăm

ecuația de gradul al doilea atunci

când se cunosc rădăcinile și o

să vedem imediat cum putem face

acest lucru o să mai scriu încă

o dată Forma generală a unei ecuații

de gradul al doilea ax pătrat plus

bx plus c egal cu 0 unde a este

diferit de 0 în continuare ne propunem

să găsim o modalitate prin care

putem să formăm ecuația de gradul

al doilea atunci când se cunosc

rădăcinile pentru aceasta vom împărți

această ecuație la a unde a este

diferit de 0 și avem a x pătrat

supra a plus b x supra a plus c

supra a egal cu 0 0 supra a este

0 aici se simplifică a și ne rămâne

x la a doua plus b supra a x plus

c supra a egal cu zero care se

mai poate scrie x la a doua minus

minus b supra a x plus c supra

a egal cu zero dar minus b supra

a este suma rădăcinilor ecuației

din relațiile lui viet iar c supra

a este produsul rădăcinilor Așadar

ecuația de gradul al doilea se

va scrie x la a doua minus x plus

b egal cu zero prin urmare atunci

când se cunosc rădăcinile ecuației

de gradul al doilea calculând suma

acestora și produsul putem să găsim

ecuația de gradul al doilea să

vedem în exemplu Să presupunem

că avem o ecuație de gradul al

doilea cu rădăcinile X1 egal cu

1 și x 2 egal cu 2 se cere să formăm

ecuația ce admit ca rădăcini aceste

două numere reale pentru aceasta

vom calcula mai întâi suma și produsul

lor suma rădăcinilor este egală

cu x 1 plus x 2 și egal cu 3 iar

produsul este X1 X2 și egal cu

2 prin urmare ecuația de gradul

al doilea se va scrie x la a doua

minus 3x plus 2 egal cu zero această

ecuație va avea rădăcinile X1 egal

cu 1 și x 2 egal cu 2 în continuare

vom discuta despre natură și semnele

rădăcinilor ecuației de gradul

al doilea în cazul în care Delta

este mai mare sau egal cu 0 atunci

ecuația de gradul al doilea admite

rădăcini reale dacă însă Delta

este negativ atunci nu avem rădăcini

reale Așadar avem rădăcini reale

atunci când vorbim despre rădăcini

reale sau nereale ne referim de

fapt la natura lor în continuare

Considerăm Delta mai mare sau egal

cu zero și ne propunem să găsim

niște reguli care ne permit să

stabilim semnul rădăcinilor ecuației

de gradul al doilea Fără a rezolva

ecuația și pentru aceasta voi scrie

niște exemple un prim exemplu Să

presupunem că avem o ecuație de

gradul al doilea având rădăcinile

X1 egal cu minus 1 și X2 egal cu

3 Haideți să calculăm suma și produsul

acestora suma este egală cu doi

Deci mai mare ca 0 iar produsul

este minus trei deci negativ observăm

Așadar că atunci când produsul

rădăcinilor este negativ rădăcinile

vor avea semne contrare Așadar

una dintre soluții este negativă

și cealaltă pozitivă însă din moment

ce sumă a acestora este pozitivă

înseamnă că modulul rădăcinii negative

este mai mic decât rădăcina pozitivă

Iată modul din minus 1 este 1 iar

unul este mai mic decât 3 încercăm

în continuare să găsim și alte

reguli care ne permit să stabilim

semnul rădăcinilor ecuației de

gradul al doilea pornind de la

semnul sumei și al produsului un

alt exemplu avem rădăcinile X1

egal cu 5 și x 2 egal cu 2 să calculăm

suma și produsul suma este șapte

Deci pozitivă iar produsul este

10 mai mare ca 0 în cazul în care

produsul a două numere reale este

pozitiv înseamnă că cele două numere

reale au același semn ia din moment

ce sumă a acestora este pozitivă

înseamnă că cele două numere sunt

pozitive Deci x-1 este mai mare

ca 0 și x 2 este mai mare ca 0

na de exemplu avem rădăcinile X1

egal cu minus 3 și x 2 egal cu

minus 2 Suma a chest ora este minus

5 negativă iar produsul este 6

pozitiv dacă produsul este pozitiv

atunci cele două rădăcini au același

semn și din moment ce sumă acestora

este negativă înseamnă că cele

două numere sunt negative Deci

x 1 este mai mic ca 0 și x 2 este

mai mic ca 0 și un al patrulea

exemplu avem rădăcinile X1 egal

minus 3 și x 2 egal cu 2 în această

situație suma este minus 1 negativă

iar produsul este minus 6 negativ

dacă produsul este negativ rădăcinile

vor avea semne contrare ia din

moment ce să mai este negativă

înseamnă că modulul rădăcinii negative

este mai mare decât rădăcina pozitivă

Iată modul din minus trei este

3 iar 3 este mai mare ca 2 am găsit

Așadar niște reguli care ne permit

să stabilim semnul rădăcinilor

ecuației de gradul al doilea pornind

de la semnul sumei și al produsului

ca să reținem aceste reguli mai

ușor le putem sintetiza intru în

tabel Iată avem cu următoarele

situații posibile dacă produsul

este pozitiv atunci rădăcinile

au același semn mai exact dacă

suma acestora este pozitivă atunci

ambele rădăcini sunt pozitive iar

dacă suma este negativă ambele

rădăcini sunt negative în cazul

în care produsul este negativ atunci

rădăcinile vor avea semn contrar

dacă suma este pozitivă atunci

modulul rădăcinii negative este

mai mic decât a doua rădăcină iar

dacă suma este negativă atunci

modul din x 1 va fi mai mare decât

x 2 putem avea și următorul caz

particular dacă suma este egală

cu 0 atunci cele două rădăcini

or avea semne contrare mai exact

X1 este egal cu minus X2 Deci avem

două numere reale opuse iar dacă

produsul este egal cu atunci fie

X1 este egal cu 0 și x 2 este egal

cu 0 să vedem în exemplu avem următoarea

ecuație de gradul al doilea 5 x

pătrat plus 14 x minus 3 egal cu

0 cerința este să stabilim natura

și semnul rădăcinilor acestei ecuații

Fără a rezolva ecuația Pentru a

stabili natura rădăcinilor trebuie

să verificăm dacă avem rădăcini

reale sau nereale pentru aceasta

vom calcula discriminantul ecuației

Delta este egal cu b pătrat adică

14 la pătrat minus 4 ori 5 ori

minus 3 și avem 196 plus 4 5 20

ori 30 și 60 egal cu 256 așa Delta

este mai mare ca 0 Prin urmare

avem două rădăcini reale și acum

Pentru a stabili semnul rădăcinilor

Fără a rezolva ecuația vom calcula

suma și produsul acestora folosind

Relațiile lui viet suma rădăcinilor

este egală cu X1 plus X2 și conform

relațiilor lui viet aceasta este

egală cu minus b supra a egal cu

minus 14 supra 5 Deci suma rădăcinilor

este negativă iar produsul acestora

X1 X2 este egal cu c supra y egal

cu minus 3 supra 5 De ce atacă

și produsul este negativ prin urmare

suntem în ultima situație produsul

negativ suma din cativa Așadar

cele două rădăcini vor avea semne

contrare x 1 este mai mic ca 0

x 2 este mai mare ca 0 și putem

să mai precizăm că modul din x

1 este mai mare decât x 2