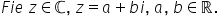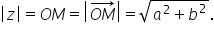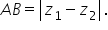Reprezentarea geometrică a numerelor complexe (aplicații)

în acest videoclip vom rezolva

următorul exercițiu Reprezentați

în planul complex multimea punctelor

de afix z pentru care au loc relațiile

la punctul a modul din z este egal

cu 4 la punctul B modul din z este

mai mic decât 6 modul din z mai

mare sau egal decât 2 modul din

z este mai mare sau egal decât

2 și mai mic sau egal decât 5 modul

din z minus 1 plus 2 y este egal

cu 3 și la punctul f 1 este mai

mic decât modul din z minus 2 plus

e și mai mic decât 4 vom rezolva

pe rând fiecare situație în parte

Și începem cu punctul A trebuie

să găsim mulțimea punctelor de

afix z pentru care modul din z

este egal cu 4 ori amintesc că

modulul unui număr complex este

distanța de la origine până la

imaginea sa geometrică astfel dacă

z este un număr complex de formă

a plus b e și notez cu m imaginea

sa geometrică atunci modul din

z este egal cu lungimea segmentului

om așa dar va trebui să găsim toate

punctele m din plan pentru care

lungimea segmentului o m este egală

cu patru iar câteva dintre acestea

însă ele nu sunt singurele deoarece

toate punctele situate pe cercul

de centru o și rază 4 respectă

această condiție ca om să fie egal

cu patru dacă vă mai amintiți cercul

era mulțimea tuturor punctelor

din plan egal depărtate de un punct

fix Așadar punctul M va Descrie

un cerc punctele de afix z pentru

care modul din z este egal cu 4

sunt punctele situate pe cercul

de centru o și raza egală cu 4

trecem mai departe la punctul b

Trebuie să găsim punctele de afix

z pentru care modul din z este

mai mic strict decât șase dacă

am fi avut egalitate adică modul

din Z egal cu șase am fi construit

un cerc de centru O și raza egală

cu șase însă din moment ce modul

din z este strict mai mic decât

6 vom construi cercul de centru

O și raza 6 Dar vom lua în considerare

doar punctele situate în interiorul

acestui cerc Așadar punctele de

afix z pentru care modul din z

este strict mai mic decât 6 sunt

punctele situate în interiorul

cercului de centru O și raza 6

continuăm cu punctul c avem modul

din z mai mare sau egal decât 2

punctele pentru care modul din

z este egal cu 2 sunt punctele

situate pe cercul de centru o și

raza egală cu 2 însă noi avem aici

modul din z mai mare sau egal decât

2 Așadar putem lua în considerare

și punctele situate în exteriorul

acestui cerc mulțimea punctelor

de afix z pentru care modul din

z este mai mare sau egal decât

2 este mulțimea punctelor de Pe

cercul de centru o și rază 2 reunite

cu punctele situate în exteriorul

acestui cerc continuăm mai departe

cu punctul d avem modul din z mai

mare sau egal decât 2 și mai mic

sau egal decât 5 prima inegalitate

se reduce la cazul precedent am

văzut că atunci când modul din

z este mai mare sau egal decât

2 avem punctele situate pe cercul

de centru o și rază 2 reunite cu

punctele situate în exteriorul

acestui cerc însă trebuie să avem

grijă ca modul din z să fie în

același timp mai mic sau egal decât

5 Așadar va trebui să mai construim

un al doilea cerc cu centrul în

origine și raza egală cu cinci

și astfel se va forma o coroană

circulară Iată cercul din interior

albastru este cercul de centru

o și rază 2 aici avem punctele

de afix z pentru care modul din

z este egal cu 2 apoi punctele

situate în exteriorul acestui cerc

sunt punctele de afix z pentru

care modul din z este mai mare

decât 2 și am fost rate al doilea

cerc de centru o și rază egală

cu cinci pentru a respecta cea

de a doua inegalitate adică modul

din z mai mic sau egal decât 5

în consecință punctele de afix

z pentru care modul din z este

mai mare sau egal decât 2 și mai

mic sau egal decât 5 sunt punctele

din coroana circulară determinată

de cercurile concentrice de centru

o și rază 2 respectiv 5 la care

se adaugă punctele acestor cercuri

mergem mai departe la punctul E

avem modul din z minus 1 plus 2

y este egal cu 3 am notat cu un

numărul complex 1 plus 2 iar m

este imaginea geometrică Așadar

m este un punct fix în plan având

coordonatele 1 respectiv 2 folosind

notația de mai sus modulul se poate

scrie astfel modul din z minus

1 este egal cu 3 dar modulul diferenței

a două numere complexe reprezintă

distanța dintre imaginile lor geometrice

dacă nu te sculam imaginea geometrică

a numărului complex z iar m este

imaginea geometrică a numărului

complex atunci modul din z minus

1 este egal cu lungimea segmentului

a m m este un punct fixat în planul

complex iar a este un punct variabil

mai trebuie să găsim toate punctele

A pentru care distanța a m este

egală cu 3 din moment ce punctul

fix este punctul M înseamnă că

va trebui să construim un cerc

cu centrul în acest punct iar raza

acestui cerc va fi egală cu 3 Iată

Așadar punctele de afix z pentru

care are loc această relație sunt

punctele situate pe cercul de centru

o și raza egală cu 3 în continuare

trecem la punctul E avem modul

din z minus 2 plus in Iar acest

model se mai poate scrie astfel

modul din z minus 2 minus e am

ales să scriem sub forma aceasta

pentru a obține în modul o diferență

dintre două numere complexe am

notat cu numărul complex 2 minus

e și atunci această inegalitate

se va scrie astfel 1 este mai mic

decât modul din z minus 1 și mai

mic decât 4 1 este numărul complex

2 minus e și am notat cu m imaginea

sa geometrică m este un punct din

plan având coordonatele 2 respectiv

minus 1 dacă nu te sculam imaginea

geometrică a numărului complex

z iar mi este imaginea geometrică

a numărului complex atunci a m

va fi egal cu modul din z minus

unu și atunci din această relație

vom obține că unul este mai mic

decât a m și mai mic decât 4 m

Este un punct fixat în plan iar

a este un punct variabil noi Trebuie

să găsim toate punctele aflate

la o distanță față de m mai mare

decât 1 și mai mică decât patru

Dacă M este punctul fixat înseamnă

că trebuie să construim un cerc

cu centrul în m iar punctele situate

față de m la o distanță mai mare

decât 1 vor fi punctele situate

în rolul cercului de centru o și

rază 1 iar punctele situate la

o distanță mai mică decât patru

ore Fie punctele situate în interiorul

unui cerc cu centrul în m și raza

egală cu 4 cu alte cuvinte trebuie

să construim două cercuri Așadar

vom obține o coroană circulară

cercul mai mic albastru este cercul

cu centrul în m și raza egală cu

unu cercul galben din exterior

este cercul cu centrul în o și

raza egală cu 4 punctele de afix

z pentru care lungimea segmentului

a m este cuprinsă între 1 și 4

sunt punctele situate în coroana

circulară determinată de cele două

cercuri