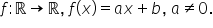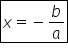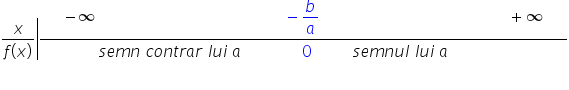Rezolvarea unor ecuații și inecuații folosind semnul funcției de gradul I

în această secvență vom rezolva

câteva ecuații și inecuații folosind

semnul funcție de gradul întâi

avem această ecuație modul din

x minus 3 plus modul din 2x plus

1 este egal cu 5 înainte de a trece

la rezolvarea ecuației aș vrea

să ne reamintim puțin explicitarea

modulului Iată Modul din a este

egal cu A dacă A este mai mare

sau egal cu 0 și minus A dacă A

este mai mic ca 0 mai întâi o să

rezolvăm ecuațiile atașat expresiilor

din modul observăm că în modul

avem expresii de gradul întâi prima

ecuație atașată este x minus 3

egal cu 0 se obține rădăcina x

egal cu trei iar a doua ecuație

2x plus 1 egal cu 0 se obține soluția

x egal cu minus 1 pe 2 vom considera

acum două funcții de gradul întâi

x minus 3 și 2x plus 1 pe care

o să le trecem întrun tabel x Avalor

de la minus infinit la plus infinit

se trec în tabel cele două rădăcini

ale ecuațiilor în ordine crescătoare

a minus 1 pe 2 și 3 funcția x minus

3 se anulează pentru x egal cu

3 iar expresia 2x plus 1 se anulează

pentru x egal cu minus 1 pe 2 funcția

x minus 3 are semn contrar lui

a până la 3:00 vă reamintesc că

a este coeficientul lui x în acest

caz a este 1 Deci pozitiv se în

contra Ba până la 3:00 și semnului

a de la 3:00 încolo funcția 2x

plus 1 are semn contrar lui a până

la minus 1 pe 2 și semnul a a pentru

valori mai mari ca minus 1 pe 2

în continuare vom considera trei

cazuri primul caz când x ia valori

cuprinse în intervalul minus infinit

minus 1 pe 2 apoi în intervalul

minus 1 pe 2 3 și în intervalul

3 infinit începem cu primul caz

x aparține intervalului minus infinit

minus unu pe doi și putem să închidem

acum intervalul în acest caz expresia

x minus trei y este negativă și

atunci va trebui să schimbăm semnul

acestei expresii la fel și expresia

2 x plus 1 este negativă și se

schimbă semnul Așadar ecuația inițială

se va scrie astfel minus pe lângă

x minus 3 minus pe lângă 2x plus

1 egal cu 5 desfacem parantezele

și avem minus x plus 3 minus 2x

minus 1 egal cu 5 minus 3X 3 minus

1 este 2 5 minus 2 3 x este egal

cu minus unu în continuare trebuie

să verificăm dacă soluția obținută

aparține acestui interval de studiu

și întradevăr minus 1 aparține

intervalului minus infinit minus

1 pe 2 Așadar soluția obținută

în acest caz va fi S1 egal cu minus

1 trecem la al doilea caz când

x aparține intervalului minus 1

pe 2 3 în acest interval expresia

x minus trei este negativă și va

trebui să schimbăm semnul însă

expresia 2x plus 1 este pozitivă

așa dar se păstrează semnul acesteia

Deci o să avem minus pe lângă x

minus 3 plus 2 x plus 1 egal cu

5 desfacem parantezele minus x

plus 3 plus 2x plus 1 egal cu 5

x plus 4 este egal cu 5 x este

egal cu 1 verificăm Dacă 1 aparține

intervalului de studiu întradevăr

1 aparține intervalului minus 1

pe 2 3 Așadar soluția obținută

în acest caz va fi S2 egal cu 1

și ultima situație dacă x ia valori

cuprinse în intervalul 3 infinit

în acest caz expresia x minus 3

este pozitivă la fel și expresia

2x plus 1 așa dar nu trebuie să

schimbăm semnul acestora Deci ecuația

inițială se va scrie x minus 3

plus 2 x plus 1 egal cu 5 Avem

3 x minus 2 egal cu 5 3 x este

egal cu 7 x egal cu 7 pe 3 7 supra

3 este 2 iar 2 nu aparține intervalului

3 infinit Așadar în acest caz soluția

va fi mulțimea vidă soluția finală

a acestei ecuații se obține reunind

cele trei soluții parțiale așa

dar esti este egal cu S1 reunit

cu S2 reunit cu s 3 și se obține

mulțimea formată din elementele

minus unu unu trecem la un alt

exercițiu avem o in ecuație 2x

minus 1 supra x plus 3 mai mare

sau egal cu 0 Așadar se cere să

aflăm acele valori ale lui x pentru

care fracția este mai mare sau

egal cu 0 observăm că atât la numărător

cât și la numitor avem expresii

de gradul întâi mai întâi o să

rezolvăm ecuațiile atașate acestora

prima ecuație 2x minus 1 egal cu

0 se obține soluția x egal cu 1

pe 2 și a doua ecuația x plus trei

este egal cu zero obținem rădăcina

x egal cu minus 3 nu am considerat

cele două funcții de gradul întâi

2x minus 1 și x plus 3 pe care

le trecem întrun tabel iar la final

avem fracția 2x minus 1 supra x

plus 3 minus infinit Infinit trecem

în tabel cele două rădăcini obținute

în ordine crescătoare a minus 3

și 1 pe 2 prima expresia 2x minus

1 se anulează pentru x egal cu

1 pe 2 apoi funcția x plus 3 se

anulează pentru x egal cu minus

3 fracția 2x minus 1 supra x plus

trei este 0 atunci când numărătorul

este 0 iar numărătorul este 0 dacă

x este 1 pe 2 în cazul în care

x este minus 3 numitorul fracției

este 0 Așadar fracția Nu are sens

pentru x egal cu minus trei și

vom trece o bară verticală studiem

acum semnul acestor funcții funcția

2x minus unu are semn contrar lui

a până la unu pe doi și semnul

lui a pentru valori mai mari ca

1 pe 2 funcția x plus 3 ale semn

contrar lui a până la minus trei

și semnului ei pentru valori mai

mari ca minus 3 iar pentru a studia

semnul acestei fracții Folosind

regula învățată la împărțire minus

cu minus este plus minus cu plus

este minus plus cu plus este Plus

noi Trebuie să aflăm care sunt

acele valori ale lui x pentru care

fracția este pozitivă observăm

că pentru x luni valori din intervalul

minus infinit minus 3 respectiv

1 pe 2 infinit fracția este pozitivă

Așadar soluția va fi intervalul

minus infinit minus trei la minus

3 punem paranteză deschisă întrucât

fracția Nu are sens pentru x egal

cu minus 3 reunit cu intervalul

1 pe 2 infinit la 1 pe 2 o să punem

paranteză dreaptă deoarece această

fracție poate fi și egală cu 0

De ce este acceptată și valoarea

1 pe 2 și un ultim exercițiu avem

următoarea inecuației modul din

x minus 1 plus modul din x minus

2 mai mare ca 5 în modul avem expresii

de gradul întâi mai întâi Rezolvă

ecuațiile atașate acestora prima

ecuație x minus 1 egal cu 0 are

rădăcina x egal cu 1 iar a doua

a ecuației x minus 2 egal cu 0

are rădăcina x egal cu doi trecem

aceste două funcții întrun tabel

prima funcției este x minus 1 iar

a doua x minus 2 minus infinit

Infinit soluțiile ecuațiilor atașate

unu și doi x minus 1 este 0 pentru

x egal cu 1 x minus doi este 0

pentru x egal cu 2 funcția x minus

unu are semn contrar lui a până

la 1:00 și semnul lui a pentru

valori mai mari ca 1 iar x minus

2 are Stan contrar lui a până la

2:00 și semnele ei pentru valori

mai mari ca doi vom lua în considerare

trei cazuri primul caz x aparține

intervalului minus infinit 1 în

acest caz expresia x minus unu

este negativă și trebuie să schimbăm

semnul acesteia Așadar inecuația

se va scrie minus pe lângă x minus

1 la fel și expresia x minus doi

este negativă Deci trebuie să schimbăm

și semnul acesteia De ce o să avem

minus pe lângă x minus 2 mai mare

ca 5 desfacem parantezele minus

x plus 1 minus x plus 2 este mai

mare ca 5 minus 2x plus 3 mai mare

ca 5 minus 2x mai mare decât doi

împărțim la minus doi atenție minus

doi este negativ se schimbă semnul

inegalității și avem x mai mic

ca minus 1 x aparține intervalului

minus infinit minus unu însă trebuie

să verificăm Dacă aceste valori

pe care îl am obținut se încadrează

în intervalul de studiu Așadar

această mulțime trebuie intersectată

cu intervalul minus infinit 1 soluția

obținută în acest caz va fi S1

egal intervalul minus infinit minus

1 trecem la al doilea cos x aparține

intervalului 1 2 în acest caz a

expresia x minus 1 este pozitivă

așa dar nu trebuie să schimbăm

semnul acesteia însă x minus 2

este negativă Deci va trebui să

schimbăm semnul o să avem x minus

1 minus x minus 2 mai mare ca 5

x minus 1 minus x plus 2 este mai

mare ca 5 se reduce x și avem 1

mai mare ca 5 ceea ce este fals

așa dar nu avem soluții în acest

caz de soluția S2 este mulțimea

vidă și în al treilea cos x aparține

intervalului 2 infinit ambele expresii

sunt pozitive așa dar se păstrează

semnul acestora și avem x minus

1 plus x minus 2 mai mare ca 5

2x minus 3 este mai mare ca 5 2x

este mai mare ca 8 x este mai mare

ca 4 x aparține intervalului 4

infinit și acest interval trebuie

intersectat cu intervalul de studiu

2 infinit intersecția acestora

va fi soluția S3 egal intervalul

4 infinit soluția finală aceste

inecuații se obține reunind cele

trei soluții S1 reunit cu S2 reunit

cu S3 și avem intervalul minus

infinit minus 1 reunit cu intervalul

4 infinit