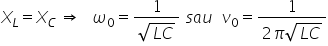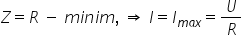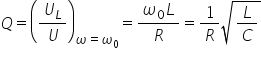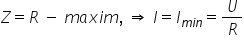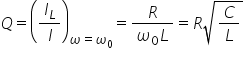Rezonanţa circuitelor RLC: frecvenţa de rezonanţă, factorul de calitate.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cea de a noua Lecție despre
curentul alternativ vom discuta
despre rezonanța circuitelor rlc
un circuit și conține reactanță
are ore XL XC ori amândouă diferite
de zero se află la rezonanță dacă
curentul e în fază cu tensiunea
în notația din lecția trecută de
faza ajul dintre curentul total
și tensiunea totală din circuit
este identic de asta în condițiile
în care avem reactanță în circuit
dacă scriem pentru curentul pentru
circuitul rlc serie formula acestei
acestui defazaj dintre tensiune
și curent și pun îl punem egal
cu zero acest de Făgăraș sau mai
exact tangenta lui obținem această
ecuație dacă facem același lucru
intru în circuit rlc paralel adică
luăm formula pentru tangenta defazajului
dintre tensiune și curent și punem
valoare egală cu 0 Puțin M această
ecuație ambele ecuații au fost
de dus în lecția precedent uitând
una la ele ambele ecuații sunt
satisfăcute Deci avem un o valoare
0 dacă x l este egal cu x c dacă
reactanța inductivă este egală
cu reactanța capacitivă din circuit
aceasta devine condiția pentru
rezonanță în circuit serie sau
paralel și în general între în
orice tip de circ uit va aduca
aminte că XL era definit ca Omega
el iar x si era definit ca unu
pe Omega c din aceste definiții
ale reactanților și această condiție
de rezonanță obținem trestia pulsații
curentului alternativ pentru rezonanță
Deci avem această egalitate când
pulsația curentului alternativ
din circuit este egal cu 1 pe radical
din orice să studiem un pic Ce
se întâmplă cu impedanță circuitului
z în în acest caz va duc aminte
că impedanță circuitului serie
rlc serie era egală cu sau este
egală cu r pătrat plus x l minus
x c la pătrat iar impedanță circuitului
paralel zapan era egală cu unu
împărțit la radical din 1 pe r
pătrat plus 1 pe x l minus 1 pe
x si y la pătrat dacă alegem valori
pentru parametrii l c și R și atunci
aceste impedanței vor fi funcție
numai de frecvență obținem cu următorul
grafic Deci ce vedeți în acest
grafic în albastru este impedanța
serie a unui circuit rlc serie
pentru care rezistență a fost fixată
la 2 RON El a fost în fixat la
un Henry și si capacitatea fost
fixată la un Deci singura variabilă
care rămâne în formula pentru z
este Omega și atunci Reprezentăm
Zet ca funcție de Omega și observăm
că în el are un minim 10 serie
are un minim pentru o valoare el
iomega de un hărți aceasta este
motivul pentru care am ales el
și C1 pentru că dacă înlocuim l
și c egal cu unu obținem frecvent
sau pulsația de rezonanță egal
cu un hack și întradevăr la un
hărți obținem un minim a lui Alin
pedanți în serie valoare impedanței
minime a circuitului serii este
egal cu doi adică este egală cu
valoarea rezistenței cu 2 m 2 pomii
și întradevăr când x l egal cu
x c z serie ar trebui și este să
fie egal cu 2 1000 Care este rezistența
dacă facem exact același lucru
pentru impedanța în paralel adică
fixăm r l și c și rămâne numai
Omega ca variabilă observăm În
graficul cu verde că impedanță
în paralel are un maxim este comportarea
invers are un maxim la la pulsația
de rezonanță care este un hărți
pentru el egal cu 1 și c egal cu
1 și la această frecvență sau pulsație
de rezonanță obținem un o valoare
a impedanței paralel egală cu 2
1000 adică egală cu valoarea rezistenței
întradevăr dacă x l egal cu x c
atunci va fi egal cu ea dar acesta
va fi un maxim și nu în minim al
impedanței în cazul circuitului
paralel în concluzie intru în circuit
rlc serie la rezonanță obținem
în minim al impedanței Care este
egal cu rezistența în concluzie
curentul care în general este împărțit
la Z la impedanță atinge un maxim
și acest maxim este egal cu o supra
aer tensiunea totală împărțită
la rezistența circuitului rlc serie
în cazul circuitului rlc paralel
la rezonanță impedanță atinge un
maxim Care este egal cu aer și
în acest caz intensitatea curentului
Care este din nou un supra Zet
tensiunea total împărțită la impedanță
va avea un minim care va fi egal
cu cu împărțit la să continuăm
studiul proprietăților circuitelor
rlc la rezonant prin introducerea
așa numitului Factor de calitate
ce este acest Factor de calitate
să ne uităm un pic la diagrama
fazorială a unui circuit rlc serie
la rezonanță am făcut diagrama
fazorială a acestor circuite de
tip era si în lecția precedent
Deci avem un circuit de răcire
la rezonanță CC după ca mama de
scris înseamnă prin definiție că
defazajul este 0 și ca și cum de
faza jul de intensitate nota lui
și curentul total și ca și consecință
pulsația va avea o valoare fixă
Care este această pulsație de rezonanță
1 pe radical din LC dacă ne uităm
la diagrama fazorială a unui circuit
rlc serie vedem că acest de fazani
dintre intensitatea totală și curentul
total este egal cu zero între o
condiție foarte specială de funcționare
a circuitului mai exact când și
y este egal cu 0 putem vedea că
el va fi egal cu usi iar adică
tensiunea pe bobină va fi egală
cu tensiunea pe condensator iar
tensiunea totală devine paralelă
cu i și cu r și Deci nu va deveni
va deveni egale cumpăr vă reamintesc
că în general pentru un circuit
rlc serie general avem următoarea
ecuație u este egal cu u r plus
cu el plus Cu ce aceasta este relația
general dar în cazul unei rezonanțe
în care este egal cu 0 Deci yasak
u u r avem situația foarte specială
său devine egal cu u a r iar el
devine egal în magnitudine dar
de semn contrar Cu ce Deci avem
o decuplare a tensiunii totale
de tensiunea pe bobină și condensator
ele devin separate ca și cum nu
ar mai fi în același circuit bineînțeles
zile sunt în același lucru Concluzia
este că wellcare este egal cu Ce
poate fi mai mare decât tensiunea
total pentru că ele nu mai sunt
legate prin aceeași cu mecanismul
prin care se poate întâmpla asta
este că circuitul oscilant bobină
condensator înmagazinează energie
în timp de la sursă și în felul
acesta poate avea o manitu o mărime
mai mare decât cea tensiune din
aceste Două ecuații o concluzie
este că în principiu putem avea
o tensiune mai mare pe bobină și
condensator decât tensionat totală
cea furnizată de sursa factorul
de calitate de scrie exact această
situație factorul de calitate sau
de supratensiune pentru în circuit
serie este definit ca raportul
dintre tensiunea pe bobină și tensiunea
totală în condiții de rezonanță
bineînțeles el poate să fie definit
și couch a împărțit la well pentru
că el este egal cu sila rezonanță
dacă înlocuim valorile u l va fi
e x l dar este același cu cel de
la de la numitor fiind râdeți se
simplifică Poate ar trebui să scriu
Deci obținem e Omega 0 al împărțit
la aer și i se simplifică în concluzie
factorul de calitate În ce serie
este Omega 0 împărțit la R putem
să facem ultimul pas înlocuind
ecuația pentru Omega 0 care este
unul pe radical din el c și obținem
că factorul de calitate este unul
pe radical din lpc în concluzie
dacă avem un circuit rlc serie
a cărui pulsație este egal cu 1
pe radical din LC adică este la
rezonanță și acest Factor de calitate
adică această combinație de parametri
r l și c este mai mare decât 1
ne aflăm în regiuni în regim de
supratensiune adică tensiunea pe
bobină și condensator tensiune
pe bobină și condensator sunt egale
și amândouă mai mari decât tensiunea
surse foarte similar se face discuția
în cazul circuitului rlc paralel
Deci avem aceeași condiție ca defazajul
dintre tensiune și curent să fie
zero numai desenez încă o dată
diagrama fazorială pentru a reusi
paralelul aveți în lecția trecută
consecința este absolut identică
ca cea pentru aerisire Cu condiția
că discutăm despre curenți în loc
de tensiuni va aduca aminte că
în cazul unui circuit AC paralel
ecuația de bază generală era că
a este egal cu e r plus e l plus
e c și la fel în cazul în care
este egal cu 0 cele două părți
ale acestei ecuații se decuplează
deci de cuplăm bobina și condensatorul
de sursă și rezistor și avem că
e l plus c egal cu zero adică au
aceeași magnitudine semnul opus
sau sens opus iar e este egal cu
e e la fel El este egal cu e c
și poate depăși e numai leagă nici
o ecuație el Și cde e direct Deci
introducem factorul de calitate
care în cazul circuitului paralel
se numește de supracurent nu de
supratensiuni si sub supracurent
în acest caz al curentului rlc
paralel dacă acest Factor de calitate
definit ca raportul dintre el și
e la frecvența de rezonanță și
egal cu această valoare dacă acest
Factor de calitate este mai mare
decât 1 atunci avem situația particulară
în care intensitatea curentului
de pe bobină și intensitatea curentului
de pe condensator sunt egale și
ambele mai mari decât intensitatea
totală a curentului din circuit
Haide să discutăm despre interpretarea
energetică a fenomenului de rezonanță
în circuit rlc pentru aceasta să
calculăm energiile pe diferitele
componente și apoi energia totală
din circuit energia magnetică este
energia înmagazinată în bobină
Deci discutăm aici despre energia
din bobina și este egală cu 1 pe
2 l l pătrat unde El este valoarea
momentană a curentului prin Boban
pe care o scriem explicit și are
această ecuație pe condensator
avem o energie electrică Care este
egală cu 1 pe 2 capacitatea condensatorului
înmulțită cu tensiunea momentan
pe condensator la pătrat aceasta
poate fi scrisă în această formă
unde am scris explicit um Deci
m pe condensator este egal cu e
m înmulțit cu x c prin Definiția
lui XC reactanța capacitivă argumentul
funcției sinus ce le scriu ceva
tensiunea pe condensator va avea
aceeași fază totală omegat a minus
fii dar defazat în spate cu piept
2 deoarece tensiunea pe condensator
este în spate cu 90 de g de față
de intensitatea prin condensator
bineînțeles prin aceasta implicăm
că ne aflăm între un circuit rlc
serie adică intensitatea de pe
condensator este egală cu intensitatea
de pe bobina și atunci defazajul
dintre aceste două funcții sinusoidale
va fi de minus pi pe 2 folosim
apoi pentru a scrie în fine ecuația
finală identitatea trigonometrică
sinus de Alfa minus fie pe A2 este
cosinus de Alfa Deci acest minus
pi pe 2 dispare Dacă transformăm
sinus încoace în cazul unui circuit
aflat la rezonanță până acum nu
am discutat despre rezonanță acestea
sunt ecuații general totuși la
rezonanță putem demonstra că aceste
valori maxime ale energiilor magnetice
și electrice sunt sa vedem deci
deci putem scrie Si XC pătrat egal
cu c 1 pe Omega la pătrat ce pătrat
aceasta este definiția lui iar
în cazul Rezonanței Omega va fi
egal cu Omega 0 care este egal
cu 1 pe radical din el si Deci
în cazul Rezonanței putem scrie
mai departe că cxc pătrat este
egal cu el adică aceste două mărimi
sunt egale în consecință în acest
caz dacă scriem energia electromagnetica
Care este suma dintre energia electrică
și energia magnetică din circuitul
rlc obținem un w0 prin care prin
w0 am notat această valoare maximă
energiei care e comună Deci am
definit 1 pe 2 L M pătrat și ia
va fi aceeași pentru ambele tipuri
de negii de ce avem w0 sinus la
pătrat de Omega termină si plus
același w0 cosinus la pătrat de
omega-3 minus și sinus pătrat plus
cosinus pătrat de același unghi
este unul eu de identitate trigonometrică
Deci obținem că w electromagnetic
energie electromagnetică este egală
cu această constant și este constantă
în circuit Haideți să Reprezentăm
grafic această funcție Deci dacă
reprezintă în grafic w e în culoarea
albastră wm în culoarea verde și
wm pentru culoarea roșie în care
pentru simplitate a graficului
am luat această valoare egală cu
Deci Vrem să vedem numai variația
cu unghiul sau cu argumentul Omega
taie cu faza Omega taie și atunci
am luat w0 Gal cu 1 atunci vedem
că variația cu faza a energiei
electrice este aceasta sinus la
pătrat a energiei magnetice este
acest cosinus la pătrat iar suma
lor este 1 Deci ceea ce observăm
și ce concluzie tragem este rezonanță
energie electromagnetică totală
oscilează între bobină și condensator
adică Pe măsură ce energia magnetică
scade Select crește cu aceeași
cantitate și invers Deci internează
între o formă electrică și una
magnetică având o sumă constantă
deci pur și simplu bobina și condensatorul
la rezonanță își schimbă între
ele energie suma totală fiind Constanța
acest fenomen de rezonanță are
foarte multe aplicații practice
una dintre cele mai cunoscute fiind
Antena antenele electromagnetice
antena radio antena TV folosesc
în Marea lor majoritate fenomenul
de rezonanță a undelor și circuitelor
electromagnetice