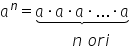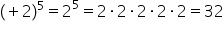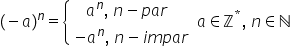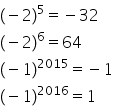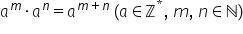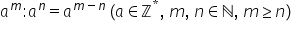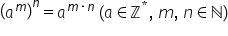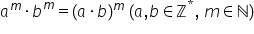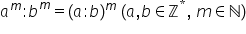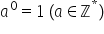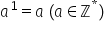Ridicarea la putere a numerelor întregi
Tag-uri
Partajeaza in Google Classroom

Transcript
ridicarea la putere a numerelor
întregi Fie a un număr întreg prin
a la puterea n înțelege în produsul
a ori a ori a de n ori a se numește
bază și m se numește exponent și
în cazul numerelor naturale ridicarea
la putere a unui număr întreg înseamnă
o înmulțire repetată a aceluiași
număr să facem un exemplu plus
3 la puterea a doua va fi egal
cu plus 3 ori plus 3 numărul plus
3 se numește bază iar 2 se numește
exponent iar rezultatul acestei
puteri va fi egal cu plus 9 adică
cu 9 ridicarea la putere a numerelor
întregi pozitive este similară
cu ridicarea la putere a numerelor
naturale deoarece numerele întregi
pozitive pot fi considerate numere
naturale să vedem ce se întâmplă
când e decum la putere un număr
negativ de exemplu minus 2 la puterea
a doua minus 2 la a doua înseamnă
minus 2 ori minus 2 minus 2 ori
minus doi este egal cu plus 4 să
vedem cât este minus 2 la puterea
a treia la fie egal cu minus 2
ori a minus 2 ori minus 2 minus
2 ori minus doi este plus 4 înmulțit
cu minus doi are va fi egal cu
minus opt să calculăm acum minus
2 la puterea a patra va fi egal
cu minus 2 ori minus 2 ori minus
2 ori minus 2 deoarece înmulțirea
este asociativă putem să înmulțim
primii doi factori și ultimii doi
minus doi ori minus doi este plus
4 înmulțit cu plus 4 iar rezultatul
va fi plus 16 și mai facem încă
un exemplu minus 2 la puterea a
cincea va fi egal cu minus 2 înmulțit
cu el însuși de cinci ori minus
2 ori minus doi este plus patru
zecimi scrie egal cu plus 4 ori
plus 4 ori minus 2 plus patru ori
plus patru este plus 16 ori minus
doi are va fi egal cu minus 32
să ne uităm puțin la aceste rezultate
observăm că minus 2 la a doua și
minus 2 la a patra este un număr
pozitiv mai exact atunci când exponentul
este un număr par rezultatul va
fi întotdeauna pozitiv Când exponentul
este impar rezultatul va fi negativ
observăm că a minus 2 la a treia
este minus 8 iar minus 2 la a cincea
este minus 32 și atunci putem să
tragem o concluzie un număr negativ
de forma minus a ridicat la o putere
n barfi egal cu a la puterea n
Deci un număr pozitiv Dacă n este
par și minus a la puterea n Dacă
n este impar în particular numărul
minus 1 la puterea n va fi egal
cu 1 Dacă n este par și minus 1
Dacă n este impar să facem și un
exemplu minus 1 la puterea a zecea
va fi egal 1 deoarece 10 este un
număr par iar minus 1 la puterea
33 va fi egal cu minus unu deoarece
and adică 33 este un număr impar
Orice număr a la puterea întâia
va fi egal cu a de exemplu în cazul
în care a este pozitiv numărul
plus 5 la puterea întâia va fi
egal cu plus 5 adică cu cinci iar
dacă numărul este negativ minus
5 la puterea întâia va fi egal
cu minus 5 0 la orice putere an
va fi egal cu 0 ori 0 înmulțit
cu el însuși de n ori a luat fie
galben departe cu 0 de 0 la orice
putere n este egal cu 0 în continuare
să vedem câteva reguli de calcul
cu puteri în cazul numerelor întregi
pozitive avem aceleași reguli valabile
ca și la numerele naturale să vedem
ce se întâmplă în cazul numerelor
întregi negative să luăm un exemplu
minus 3 la puterea a doua ori minus
3 la puterea a treia Dorin se obține
o formulă Generală de calcul pentru
acest produs să vedem ce o să se
întâmple cu exponenții în cazul
unui produs de două puteri cu aceeași
bază minus 3 la puterea a doua
a conform definiției este minus
3 ori minus 3 minus 3 la a treia
semne minus 3 ori minus 3 ori minus
3 observăm că factorul minus 3
apare de cinci ori în acest produs
deci putem scrie egal cu minus
3 la puterea a cincea ne uităm
puțin la exponenți observam ca
exponentul rezultatului este suma
dintre cei doi exponenți și atunci
Putem să scriem o regulă Generală
de calcul a la puterea M ori a
la puterea n va fi egal cu a la
puterea m plus n să mai luăm un
alt exemplu minus 5 la a patra
împărțit la minus 5 la a doua deoarece
împărțire a poate fi scris și sub
forma unei fracții această împărțire
putem să o scriem astfel minus
5 ori minus 5 ori minus 5 ori minus
5 adică minus 5 la a patra supra
minus 5 ori minus 5 adică minus
5 la a doua putem să simplificăm
cu minus 5 deoarece el Apare și
la numărător și la numitor și de
asemenea mai putem să mai simplificăm
odată cu minus 5 iar rezultatul
va fi minus 5 ori minus 5 supra
1 pe care no să mai scriu iar minus
5 ori minus 5 este egal cu minus
5 la puterea a doua observăm că
exponentul rezultatului este diferența
dintre cei doi exponenți și atunci
putem trage următoarea concluzie
a la puterea m împărțit la a la
puterea n este egal cu a la puterea
M minus n să vedem ce se întâmplă
dacă m este egal cu m să calculăm
minus 3 la puterea a șaptea împărțit
la minus 3 la puterea a șaptea
conform formulei de mai sus acest
lucru va fi egal cu minus 3 la
puterea 7 minus 7 Care este egal
cu minus 3 la puterea 0 dar știind
că atunci când împărțim un număr
la el însuși Rezultatul este unul
Deci minus 3 la puterea zero va
fi egal cu unu și atunci Putem
afirma că orice număr a ridicat
la puterea 0 va fi egal cu 1 să
vedem cum se poate scrie puterea
unei puteri Venus 2 la puterea
a doua și totul ridicat la puterea
a treia minus 2 la a doua înseamnă
minus 2 ori minus 2 și totul ridicat
la puterea a treia a ridica un
produs la puterea a treia înseamnă
l înmulțit cu el însuși de trei
ori de circo ma vrea a egal cu
minus 2 ori minus 2 ori minus 2
ori minus 2 ori minus doi ori minus
doi Deci acest produs lemon mulți
cu el însuși de trei ori observăm
că factorul minus doi apare de
șase ori în acest produs și atunci
Putem să scriem egal cu minus doi
la puterea a șasea observăm că
exponentul rezultatului este produsul
dintre cei doi exponenți și atunci
Putem să scriem următoarea formulă
a la puterea m totul la puterea
n va fi egal cu a la puterea n
ori n și un ultim exemplu minus
2 ori minus 4 totul ridicat la
puterea a doua dorim să obținem
o formulă de calcul fără a face
calculul din paranteză minus două
ore minus 4 ridicat la puterea
a 2-a înseamnă minus 2 ori minus
4 ori minus 2 ori minus 4 deoarece
înmulțirea este comutativă Putem
să schimbăm locul acestor factori
și să scrie m egal cu minus 2 ori
minus 2 ori minus 4 ori minus 4
Dar vinul doi ori minus doi este
minus 2 la puterea a doua iar minus
4 ori minus 4 este minus 4 la puterea
a doua observa mașina dar că exponentul
inițial se distribuie la fiecare
Factor al produsului și atunci
Putem să scriem încă o formulă
și anume a ori b la puterea n este
egal cu a la m ori b la m să rețineți
aceste reguli de calcul cu puteri
o să le mai citesc o dată a la
m ori a la n este egal cu a la
puterea m plus n m împărțit la
a la n este egal cu a la puterea
n minus n a ori b totul la puterea
m este egal cu a la n ori b la
m iar ala am ridicat la puterea
n este egal cu a la puterea M ori
unde în continuare să facem câteva
exerciții primul exercițiu punctul
a plus 2 la puterea a treia 2 la
puterea a treia este egal cu 8
cum am spus și mai devreme a ridicarea
la putere a numerelor întregi pozitive
este similară cu ridicarea la putere
a numerelor naturale Deci nu voi
insista cu exemple de genul acesta
să facem câteva exemple cu numere
negative minus 3 la puterea a treia
deoarece exponentul este impar
atunci când ridicăm un număr negativ
la o putere impară Rezultatul este
negativ Deci pune mai întâi semnul
minus iar 3 la a treia este 27
următorul exercițiu minus 7 la
puterea a doua un număr negativ
la putere pară este pozitiv iar
7 la a doua este 49 minus 7 la
a doua trebuie să facem distincție
între minus 7 la a doua scris în
paranteză și minus 7 la a doua
scris fără paranteză în primul
caz adică la punctul C se ridică
la puterea a doua a numărul negativ
minus 7 iar în acest caz Rezultatul
este pozitiv la punctul b se ridică
la puterea a doua doar numărul
7 Iar semnul minus se copiază și
atunci rezultatul va fi minus 49
punctul f minus patru la puterea
a treia un număr negativ la putere
impară va fi negativ iar patru
la puterea a treia este 64 minus
8 la puterea a 6-a împărțit la
minus 8 la puterea a patra am folosit
2-a regulă de calcul cu puteri
și vom scrie egal cu minus opt
la puterea 6 minus 4 adică minus
8 la a doua care va fi egal cu
plus 64 minus 5 ori minus 5 la
puterea a doua primul Factor minus
5 are exponentul 1 atunci când
nu este scris exponentul unei puteri
si subînțelege că el este unul
Și atunci vom folosi prima regulă
de calcul cu puteri și vom scrie
egal cu minus 5 la puterea 1 plus
2 adică minus 5 la a treia exponentul
fiind din par pune minus 5 la a
treia este 125 și ultimul exemplu
minus 3 la puterea 16 împărțit
la minus 3 la puterea a patra și
totul la puterea a treia ma fie
egal cu minus 3 la puterea 16 împărțit
la minus 3 la puterea 4 ori 3 folosim
ultima formulă 4 x 3 este 12 și
egal mai departe cu minus 3 la
puterea 16 minus 12 adică minus
3 la a patra numărul 4 fiind număr
par rezultatul va fi pozitiv iar
trei la puterea a patra este 81