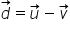Scăderea vectorilor

scăderea în general este operația

prin care adunăm la descăzut opusul

scăzătorului în mod Analog o să

definim și scăderea vectorilor

vectorul a minus vectorul b va

fi egal cu vectorul a adunat cu

opuse vectorului b Așadar scăderea

vectorilor înseamnă adunarea descăzutul

lui cu opusul scăzătorului Haide

să construim opusul vectorului

b yatour Acesta este un Vector

având aceeași direcție cu b același

modul dar sensuri opuse pentru

a aduna vectorul a cu vectorul

minus b vom folosi regula paralelogramului

o să ducem Așadar paralele la direcțiile

celor doi vectori iar diagonala

acestui paralelogram va fi și rezultatul

sumei prin urmare vectorul a adunat

cu vectorul a minus b va fi diagonala

paralelogramului o c dacă c b prim

o a este un paralelogram atunci

Segmentul ce am este congruent

cu B prim o dar B prim o este congruent

cu segmentul o b din construcția

făcută prin urmare segmentul c

n este congruent cu OB cele două

drepte sunt și paralele Așadar

c o b a este tot un paralelogram

iar prin urmare segmentele c o

și a b sunt congruente așa Dar

cei doi vectori vor fi vectori

egali a având același modul același

sens și aceea direcție așa dar

putem să scriem că vectorul o A

minus vectorul o b este egal cu

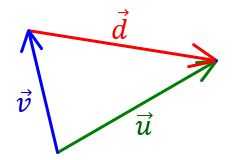
vectorul b a Observați că vectorul

diferență are săgeata îndreptată

spre descăzut în general când trebuie

să efectuăm scăderea a doi vectori

uși vă luăm așezat cei doi vectori

astfel încât aceștia să aibă originea

comună iar vectorul diferență se

obține un in de extremități a celor

doi vectori Iată iar extremitate

a vectorului diferență va fi întotdeauna

orientată spre vectorul descăzut

Așadar u A minus V este egal cu

d și acum să facem o aplicație

avem punctele a b c d și m și vectorul

AD se cere să scriem acest Vector

ca o diferență de doi vectori va

trebui să găsim doi vectori care

au originea comună iar extremitatea

descăzutul lui să fie în punctul

de o primă variantă ar fi aceasta

CD minus si ei Așadar vom scrie

adem vectorul AD este diferența

vectorilor cd și ce a o altă variantă

posibilă ad se poate scrie ca fiind

diferența dintre vectorii b d și

b a sau o altă variantă posibilă

Iată Ade este diferența vectorilor

a d și e a să reținem Așadar că

diferența a doi vectori este un

Vector care se obține un in de

extremități a celor doi vectori

având originea comună iar extremitatea

a vectorului diferență coincide

cu extremitatea descăzutul lui