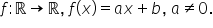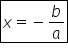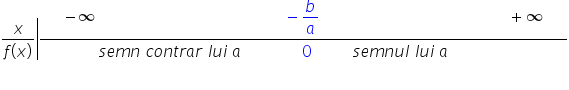Semnul funcției de gradul I

semnul funcției de gradul întâi

are o aplicație deosebită în rezolvarea

unor ecuații cu modul respectiv

a unor inecuații a studia semnul

funcție de gradul întâi înseamnă

a determina acele valori ale lui

x pentru care funcția este pozitivă

respectiv Găsirea celor valori

ale lui x pentru care funcția este

negativă dacă Privim aceste exemplu

observăm că Pentru anumite valori

ale lui x fracția este pozitivă

pentru că graficul acesteia este

situată deasupra axei o x iar pentru

anumite valori ale lui x fracția

este negativă deoarece graficul

acesteia este situat sub axa o

x observăm că până în acest punct

funcția este pozitivă iar de la

acest punct încolo funcția este

negativă așa Dar acest punct are

o importanță deosebită în studiul

semnului funcție de gradul întâi

Forma generală a unei funcții de

gradul întâi f de x este egal cu

ax plus b unde a este diferit de

zero pui nota acest punct cu a

dat fiind faptul că el este situat

pe axa o x ordonat acestui punct

va fi 0 iar pentru a găsi abscisa

punctului se rezolvă ecuația f

de x egal cu 0 mai exact ax plus

b egal cu 0 de unde rezultă x egal

cu minus pe supra a așa Dar acest

punct va avea coordonatele minus

b supra a 0 în acest exemplu pentru

x luni valori mai mici decât minus

b supra a funcția este pozitivă

iar pentru x mai mare ca minus

b supra a funcția este negativă

să vedem acum concret cum vom studia

semnul funcției de gradul întâi

8 să dea mai întâi cazul în care

a este pozitiv și vrem să vedem

Ce semn are funcția în cazul în

care x este mai mic decât minus

b supra a respectiv x mai mare

decât minus b supra a dacă x este

mai mic decât minus b supra a înmulțit

toate inegalitatea cu a ei fiind

pozitiv se ajunge la următoarea

inegalitate a x mai mic decât minus

pe vreau să ajung la Forma generală

a funcției de gradul întâi pentru

a vedea semnul acesteia obțin a

x plus b mai mic ca 0 prin urmare

f de x este mai mic ca 0 observăm

Așadar că funcția f are semn contrar

lui a pentru x mai mic decât minus

b supra a Iată a este pozitiv fdx

negativ așa dar putem să scriem

f arestăm contra lui a să vedem

ce se va avea funcția în cazul

în care x este mai mare decât minus

b supra a înmulțim inegalitatea

cu a și obținem a x mai mare decât

minus b adică ax plus b mai mare

ca 0 800 Roma Așadar că fdx este

mai mare ca 0 pentru x mai mare

ca minus b supra a cu alte cuvinte

e f are semnul lui a să vedem ce

se întâmplă în cazul în care a

este negativ vom studia semnul

funcției în cazul în care x este

mai mic decât minus b supra a respectiv

x mai mare decât minus b supra

a înmulțim inecuația cu a atenției

este negativ Așadar se schimbă

semnul inegalității obținem a x

mai mare ca minus b ax plus b mai

mare ca 0 Așadar f de x este mai

mare ca 0 pentru x mai mic ca minus

b supra a a este negativ fdx este

pozitiv putem trage concluzia că

e f are semn contrar lui a procedăm

la fel și aici înmulțim inecuația

cu a și obținem ax plus b mai mic

ca 0 adică f de x mai mic ca 0

Așadar f are semnul lui a în concluzie

observăm că dacă x este mai mic

ca minus b supra a f are semn contrar

lui a indiferent dacă a este pozitiv

sau negativ în ambele situații

am obținut că e f are în contra

lui a pentru x mai mic ca minus

b supra a iar pentru x mai mare

ca minus b supra a funcția f are

semnului a Iată indiferent dacă

a este pozitiv sau negativ funcția

f are semnului a pentru Islam valori

mai mari ca minus b supra a putem

să scriem aceste concluzii întrun

tabel Așadar pentru a reține mai

ușor semnul funcție de gradul întâi

vom face un tabel avem x și f de

x x y Avalor de la minus infinit

la plus infinit soluția ecuației

atașate este minus b supra a acesta

se mai numește și zeroul funcției

pentru x luni valori mai mici ca

minus b supra a funcția f de x

are semn contrar lui A iar pentru

x mai mare ca minus b supra a funcția

are semnul lui a să vedem concret

un exemplu avem funcția f definită

pe r cu valori in r f de x egal

cu 3 x plus 6 Săcele să studiem

semnul acestei funcții mai întâi

rezolvăm ecuația atașată 3x plus

6 egal cu 0 se obține soluția x

egal cu minus 2 Și acum să facem

tabelul avem pe prima linie x și

pe a doua linie f de x x Avalor

de la minus infinit la plus infinit

soluția ecuației este minus 2 iar

pentru x egal minus 2 f de x este

0 în acest caz a este 3 Așadar

a este mai mare ca 0 pentru x lung

valori mai mici ca minus 2 funcția

are semn contrar lui a adică minus

iar pentru x luni valori mai mari

ca minus doi funcția are semnului

ei adică plus și atunci putem se

trage următoarele concluzii dacă

x aparține intervalului minus infinit

minus 2 atunci funcția f de x este

negativă dacă x aparține intervalului

minus 2 infinit f de x este mai

mare ca 0 iar pentru x egal cu

minus 2 f de x este egal cu 0 să

vedem un alt exemplu avem funcția

f definită pe r cu valori in r

f de x egal cu minus 3x plus 2

rezolvăm ecuația atașată minus

3x plus 2 egal cu 0 obținem minus

3x egal cu minus doi de unde rezultă

x egal cu 2 pe 3 face tabelul de

semn x f d x minus infinit plus

infinit soluția ecuației 2 pe 3

f în 2 pe 3 este 0 a este negativ

Haideți scrie ma Aici este minus

3 adică mai mic decât 0 pentru

exatlon valori mai mici ca 2 pe

3 funcția are semn contrar lui

a adică plus iar pentru x mai mare

ca 2 pe 3 funcția are semnului

ei adică minus Și atunci vom scrie

pentru x aparținând intervalului

minus Infinit 2 pe 3 avem f de

x mai mare ca 0 pentru x valori

de la 2 pe 3 la infinit funcția

este negativă iar pentru x egal

cu 2 pe 3 funcția x este egală

cu 0 în continuare mai facem un

exercițiu se cere să stabilim semnul

expresiilor la punctul a avem expresia

e de x egal cu 3 minus x supra

x plus 2 unde x este diferit de

minus 2 iar la punctul B avem expresia

e de x egal cu x pe lângă x minus

2 pe lângă x plus 4 pentru a studia

semnul acestei expresii vom considera

două funcții F și G definite pe

r cu valori in r f de x este 3

minus x și g de x este egal cu

x plus 2 funcții întrun tabel avem

pe prima linie x pe a doua linie

f de x egal cu 3 minus x apoi g

de x egal cu x plus 2 și toată

fracția e de x egal cu 3 minus

x supra x plus 2 să rezolvăm ecuațiile

atașate trei minus x este egal

cu 0 pentru x egal cu 3x plus 2

este egal cu 0 pentru x egal cu

minus 2 trecem aceste două valori

în tabel în ordine crescătoare

avem minus infinit minus 2 3 și

plus infinit Pentru x egal cu 3

funcția f de x este egală cu zero

pentru x egal cu minus 2 g de x

este egal cu zero pentru x egal

cu 3 e de x este 0 iar pentru x

egal cu minus 2 fracția Nu are

sens și vom scrie aici o bară verticală

nu folosiți semnul funcție de gradul

întâi atât pentru funcția f de

x cât și pentru funcția g de x

f de x este 3 minus x așa dar ei

este negativ are semn contrar lui

a până la 3:00 adică plus și s

are semnul lui a de la 3:00 încolo

adică minus trecem la a doua funcție

de x egal cu x plus 2 în acest

caz a este 1 Deci pozitiv gdx are

Stem contra lui ei până la minus

doi adică minus și semnul lui a

pentru x lui valori mai mari ca

minus 2 Pentru a stabili acum semnul

aceste expresii Folosind regula

semnelor învățate la înmulțirea

și împărțirea numerelor reale plus

cu minus este minus plus cu plus

este Plus și minus cu plus este

minus Și acum uitând de pe ultima

linie a tabelului observăm că e

de x este mai mic ca 0 pentru x

rând valori de la minus infinit

la minus 2 punem paranteză rotundă

la minus doi pentru că expresia

Nu are sens pentru x egal cu minus

2 reunit cu intervalul 3 infinit

și la 3 punem paranteză rotundă

pentru că ne interesează cazul

în care e de x este strict mai

mic ca 0 vom studia separat cazul

în care e de x este 0 apoi e de

x este mai mare ca 0 pentru x luni

valori de la minus 2 la 3 și e

de x este egal cu zero pentru x

egal cu 3 e de x nu este definită

sau nu are sens pentru x egal cu

minus 2 Și acum continuăm cu punctul

B avem expresia e de x egal cu

x pe lângă x minus 2 pe lângă x

plus 4 pentru a studia semnul expresii

de la punctul B Considerăm trei

funcții f g și h definite pe r

cu valori in R astfel f de x egal

cu x g de x egal cu x minus 2 și

HD x egal cu x plus 4 mai întâi

rezolvăm ecuațiile atașate pentru

fiecare în parte f de x este egal

cu 0 Dacă și numai dacă x este

egal cu 0 apoi g de x este 0 pentru

x egal cu 2 și HD x este 0 pentru

x egal cu minus 4 trecem aceste

valori întrun tabel pe prima linie

avem x apoi f de x egal cu x urmează

g de x egal cu x minus 2 HD x egal

cu x plus 4 și e d x adică produsul

x pe lângă x minus 2 pe lângă x

plus 4x Avalor de la minus infinit

la plus infinit trecem zerourile

funcțiilor în ordine crescătoare

avem minus 4 0 și 2 f se anulează

pentru x egal cu zero G se anulează

pentru x egal cu 2 H se anulează

pentru x egal cu minus patru de

x este un produs de trei factori

iar un produs poate fi 0 dacă oricare

dintre factori este 0 Așadar e

de x este 0 dacă x este minus patru

zero sau doi și Acum începem cu

studiul semnului funcției fdx în

cazul funcția fdx a este 1 Deci

pozitiv efr semn contrar lui a

până la zero adică minus și semnul

lui a pentru x mai mare ca 0 G

de x este x minus doi deci a este

1 pozitiv g de x are semn contrar

lui a până la 2:00 adică minus

și semnul lui a pentru x mai mare

ca 2 HT x este x plus 4 a este

pozitiv semn contrar lui a înseamnă

minus semnului a plus folosim iarăși

regula semnelor Produsul a trei

numere negative este negativ apoi

avem minus ori minus ori plus înseamnă

Plus plus ori minus ori plus este

minus iar plus ori plus ori plus

este plus o Scrie mai jos concluziile

observăm că e de x este mai mic

ca 0 pentru x rând valori de la

minus infinit la minus 4 Iată reunit

cu 0 2 Pune paranteze rotunde pentru

că studiem separat cazul în care

ad x este 0 apoi e de x este mai

mare ca 0 pentru x luni valori

în intervalul minus patru zero

reunit cu 2 infinit Iar e de x

este egal cu 0 dacă x aparține

mulțimii minus 4 0 sau doi pentru

o secvență următoare vom rezolva

câteva ecuații și inecuații folosind

semnul funcției de gradul întâi