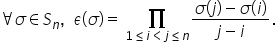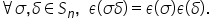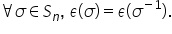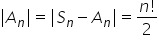Semnul produsului a două permutări

pentru a putea găsi o exprimare

a semnului produsului a două permutări

vom pornind de la următorul exemplu

Să considerăm Sigma o permutare

de grad 4 Sigma egal cu 1 2 3 4

cu imaginile 3 1 4 2 8 considera

următoarele produse Sigma de 2

minus Sigma de 1 supra 2 minus

1 Sigma de 3 minus Sigma de 1 totul

supra 3 minus 1 Sigma de 4 minus

Sigma de 1 totul supra 4 minus

1 Sigma de 3 minus Sigma de 2 totul

supra 3 minus 2 Sigma de 4 minus

Sigma de 2 totul supra 4 2 înmulțit

cu Sigma de 4 minus Sigma de 3

totul supra 4 minus 3 acest produs

în cazul acestei permutări ia următoarea

value Pack Sigma de 2 este unul

Sigma de 1 este 3 Adică 1 minus

3 supra 2 minus 1 Sigma de 3 este

4 iar Sigma de 1 este 34 Venus

3 supra 3 minus 1 Sigma de 4 este

2 iar suma de 1 este 3 Deci 2-a

minus 3 supra 4 Sigma de 3 este

4 Sigma de 2 este 1 4 minus 1 supra

3 minus 2 Sigma de 4 este 2 Sigma

de 2 este un 2 minus 1 supra 4

minus 2 Sigma de 4 este 2 iar Sigma

de 3 este 4 Deci 2 minus supra

4 minus 3 observăm următorul lucru

fiecare dintre numărătorii acestor

cinci fracții se regăsesc printre

numitorii aceste fracții cu excepția

unui sân concluzii diferența 1

minus 3 se regăsește la numitorul

fracției următoare dar este desen

schimbat se pot simplifica aceste

expresii Ținând la Unul dintre

factori minus 1 de asemenea 4 minus

3 se poate simplifica cu 4 minus

3 2 minus 3 se simplifică la fel

cu 3 minus 2 rămânând aici minus

1 4 minus unu cu patru minus unu

doi minus unu cu doi minus unu

iar 4 minus 2 cu 2 minus 4 rămânând

aici minus 1 avem produsul minus

1 minus 1 ori minus unu adică minus

1 la puterea a treia minus 1 Pe

de altă parte inversiune la aceste

permutări sunt următoarele perechea

1 2 face inversiune pentru că 3

este mai mare decât 1 perechea

1 3 nu face inversiune pentru că

3 este mai mic decât 4 1 4 da pentru

că 3 este mai mare decât doi doi

nu face inversiune nici cu 3 nici

cu patru îmi schimbai avem voi

în versiunea 3 4 în total m de

sârmă este egal cu 3X Alin de Sigma

este minus 1 totul la puterea a

treia dacă am generaliza pentru

o permutare Sigma din Sen se poate

demonstra epsilon de Sigma de fapt

este un produs de fracții de tipul

acesta adică un produs după 1 mai

mic sau egal decât y mai mic decât

z mai mic sau egal decât n din

fracții de forma Sigma de z minus

Sigma a supra minus folosind această

relație să încercăm să găsim o

expresie a semnului produsului

a două permutări epsilon de Sigma

ori de alta ar fi un dus după 1

mai mic sau egal decât y mai mic

strict decât z mai mic sau egal

decât n Sigma de Delta DJ minus

Sigma de Delta de i j acest produs

îl putem exprimă și astfel 1 mai

mic sau egal decât y mai mic decât

z mai mic sau egal decât n Sigma

de Delta DJ minus Sigma de Delta

D supra Delta DJ minus Delta înmulțit

cu fracția Delta DJ minus Delta

D supra j Minu Ce observați că

fracția inițială nu sa modificat

prin inserarea acestei diferențe

în schimb folosind faptul că înmulțirea

numerelor reale este o operație

asociativă acest produs îl putem

Rescrie astfel produs după 1 mai

mic sau egal decât y mai mic decât

z mai mic sau egal decât n din

Sigma de Delta DJ minus Sigma de

Delta D supra Delta DJ minus Delta

de înmulțit cu produs după 1 mai

mic sau egal mai mic decât z mai

mic sau egal decât n din Delta

DJ minus Delta de supra j Manuc

Păi primul produs nu reprezintă

altceva decât epsilon de Sigma

iar cel de al doilea produs nu

reprezintă altceva decât salon

de Delta am obținut astfel relația

epsilon de Sigma ori Delta este

egal cu EF salon de Sigma înmulțit

cu ieftin de Delta Sigma Sigma

la minus 1 este permutarea identică

Iceland Sigma orie psiland Sigma

la minus 1 este egal cu unu adică

nu poate fi decât ambele unu sau

minus unu ieftin de Sigma este

egal cu epsilon de Sigma la minus

1 am văzut că o permutare poate

fi pară sau impară ar fi interesant

să știm Câte permutări pare sau

impare există în esență notăm cu

A indice n mulțimea permutărilor

pare Cum ies an era mulțimea tuturor

permutărilor iese n minus a n reprezintă

mulțimea permutărilor impare Dacă

vom considera Sigma o permutare

pară Deci o permutare din a indice

n produsul dintre transpoziția

Asia și Sigma este o permutare

impară Deci aparține lui ethan

minus Ioan funcția care Asociază

pe mutării Sigma permutarea Delta

i j Wars Sigma este o funcție definită

pe mulțimea a n cu valori în mulțimea

s n minus iar această funcție este

o funcție bijectivă fiind o funcție

bijectivă cardinalul mulțimii A

n este egal astfel cu cardinalul

mulțimii s n minus Ioan Cum cardinalul

lui ecn este Ioan factorial de

ducem astfel că numărul permutărilor

pare este n factorial supra 2 și

este egal cu numărul permutărilor

impare